2.1 La phase cohésive :
Lorsque T.. ? 0. c a d 0 < T.. <
T, , T, est la charge de rupture, la fissure doit
apparaître (figure 2.3) d'une façon a ce que la contrainte de
cisaillement maximale dans le corps soit inférieur de la valeur critique
Tc . Par conséquent le FIC k3 en la
pointe de la fissure doit être
nul. Lorsque la charge est suffisamment proche du zéro,
la longueur de la fissure est
suffisamment petite de tel sort que l'ouverture
[if ] est partout inférieure à la valeur
critique äc. En conséquence,
toute les lèvres de la fissure crée sont soumise a une force
cohésive d'intensité Tc, et le champ de
déplacement ainsi que le champ de contrainte a l'équilibre sous
le chargement T.. sont donc solution du problème suivant :
x2

x3
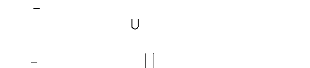
=
A TV
II /(D U F)
D
=-2.0
2n
2n=2 a
=#177;
=
x2
223
~
~~ ~ ~
~ ~
dans
sur
sur
sur
0
n
n
0
F
F
h
(2.8)
x1
h
-
la
-
l0
l0
la
h
Figure 2.3. Géométrie de la bande avec les
chargements dans la phase cohésive.
Les pointes x1 = #177;la de la zone
cohésive avance est de façon a ce que la contrainte
223 ne dépasse jamais la valeur critique
2a dans la structure, cela oblige donc que les contraintes ne
soient pas singulières aux points x1 = #177;la de
l'axe x2 = 0 .
Par conséquent, la loi gouvernant l'évolution des
pointes #177; la de la fissure avec le chargement est k3
(#177;la ) = 0.
En d'autre terme, l'énergie total restitué G due a
la fissure cohésive crée doit être nul.
Cette phase cesse lorsque l'ouverture[-kt, ] aux points
x1 = #177;la dépasse la valeur critique
êa ceci
(2.9)
signifie qu'une fissure non cohésive doit
apparaître, la valeur du chargement correspondante est appelé la
charge de rupture, elle est défini par :

2r= sup{2 > 0 : [TV
](l0) <Val
2.2 La phase de propagation :
Si la charge est augmenté au-delà
deir , le corps ne peut pas trouver l'équilibre sans
qu'il y'a initiation et propagation d'une pointe non cohésive de la
fissure crée. Ainsi, la fissure F doit se diviser en deux partie une
partie cohésive Fa est une non cohésive F0.
On note par
la et la leur pointes respective (figure
2.4).
x2
x3
h
-
la -
la
-
l0
l0
la la
h
x1
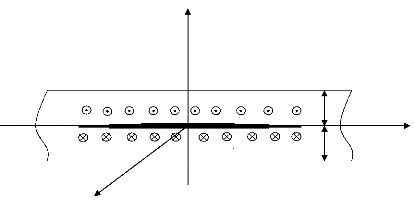
Figure 2.4. Géométrie de la bande avec les
chargements dans la phase propagation.
(2.10)
On a donc :
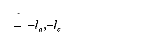
Ù0 = Ù/( F),F
DU =F0 UFa
.
x {OU ya , la ) x {0l.
= (- x {0} U y0 , la ) x {0l.
,
l
0
l
a
F0
l
l
(
Fa
Le champ de déplacement w et de contrainte i ,
doit satisfaire les équations suivantes :
0
0
dans
A W
Ù
a
n
sur
in = ia
0
i23
sur
~
~~ ~ ~
~ ~
D U F
(2.11)
x2 =#177; h
Fa
in = -i8 n sur
Les lois gouvernants l'évolution des pointes #177;
le et #177; la sont donné par :
|
k3 (#177;la ) = 0,
|
[w
|
](#177;le)
|
=
|
äe
|
.
|
(2.12)
|
| 


