1.4 Demi plan contenant une fissure rectiligne [21]
:
Dans ce cas on considère un demi-plan SI = (--...,+.0)x
(--..., h), contenant un défaut de type fissure
D=[--l0,l0]x{0} de longueur 2l0
parallèle et distant de h de la face supérieure du domaine. Le
milieu est élastique isotrope caractérisé par un module de
cisaillement, . Sur la face supérieure x2 = h et
à l'infini x2 --o. est appliqué un cisaillement
anti-plan uniforme et positift_ , les lèvres de la fissure sont
libres. La seule composante de déplacement est dans la direction x3.
x1
L'évolution de la fissure pendant le chargement sous
l'effet du cisaillement anti-plan appliqué suit la loi de
DUGDALE-BARENBLATT.
1-8
h
-
10
10
x3
1-8
x2
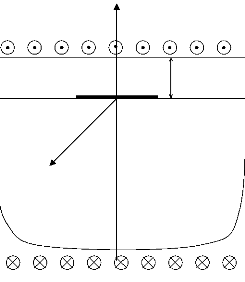
Figure 1.19. La charge et la géométrie du
problème original.
x2
1-(x1)
h
x1
-
1a
-
10
10
1a
x3
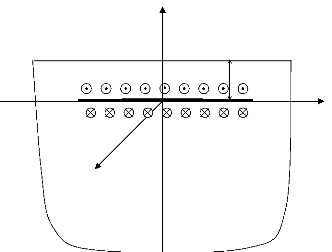
Figure 1.20. Le problème durant la phase
cohésive.

l0
si
x1
(1.1)
<
si
la
l0
< x1
34
Le chargement r(x1) est donné par
:
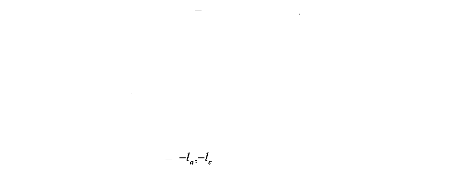
Le problème élastique constitué par les
équations d'équilibre et les conditions aux limites dans la phase
de propagation, est donné par le système suivant :
0
=
0
dansf2
A W
C
r.n=-r..
.n su
r1-2
r.n=rC
.n sur
FC
r23
= 0 surx2 = h
x2 --,-..
x
2
lim r13 = 0, lim r23 =
0
->--
srC = SII(D U F), F = F0 U FC
X MU [lC , la ) X M.
, l
0
F0 = (- X MU [4 jC)X{0}
~ ~
~~ ~ ~
~
~ ~
.
lC
l
l
(
=
FC
0
C
Avec :
(1.2)
(1.3)
Les loi gouvernant l'évolution des pointes
cohésives #177;lC et #177; la sont donnée
par :
k3(#177;la)= 0,
Le système d'équations (1.2) ainsi établie
est réduit à une équation intégrale
singulière, cette transformation se fait en appliquant les
transformations de fourrier standard.
L'équation intégrale singulière est
donnée par :
tia
r 1
L + k(x1,t)W(t).dt = 21t
r(x1 ),
t
x1
Il-
la
Avec : fv(t).dt = 0 (1.5bis)
-l
Ou la fonction k(x1,t) et donné par :
k (
2 (1.6)
t - x1
x1, t) =
4h2 + (t- x1) -la,-lC L'inconnue
u(t) est une fonction densité définie par :
w(t)= at [W(t,0+)- W(40)] (1.7)
A fin de résoudre l'équation intégrale on
doit introduire les quantités normalisées suivante :
x1
r= , s= ,
10 10
v(t) = f (s), k(x1,t) = L(r, , s), r
(x 1) = r(r) (1.8)
t
4
17 = 10

L'équation intégrale se réduit a :
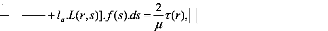
1
r
(1.9)
1
+
1
1
71-
f[ s
1
r
Avec la condition
+ 1
ff (t).dt = 0 (1.10)
1
A cause des discontinuités dans la distribution des
chargements due au modèle de
DUGDALE-BARENBLATT, la méthode de
résolution standard ne donne pas de bon
résultat.
L'idée est de remplacer la fonction inconnue f (s)
par f (s) = h(s) +0(s) , où h(s) est la
solution de l'équation suivante :
1+1 f1
1 s -- r
2
ds = r(r),
il
h(s)
71-
1
r <1
(1.11)
Avec :
+ 1
f h(s)ds = 0. (1.1 1bis)
1
0(s) est solution de :
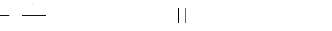
+
1
1
<1
r
s ds
f[s
( ) (r)
,
g
71-
r
1
1
+ 1 aL(r, s
)]0
(1.12)
Avec :
+ 1
1
g(r) = -- f1 aL(r, , s).h(s)ds 71-
(1.12 bis )
+ 1
(t)dt
0
f0
1
La méthode standard de résolution consiste à
exprimer 0(s) sous la forme0(s) = W(s)v(s) , ou
1
2)
(S )
(1
W = -s 2 sont les fonctions poids associés aux
polynômes de CHEBYSHEV du
+ 1 a .L(r , s)]. f (s).ds = 2 r(r),
il
premier ordre Tn (s) = cos(n.ar cos(s)) et
e(s) est une fonction continue et limitée sur
l'intervalle [--1,1] qui peut être exprimé avec une
série tronqué des polynômes de CHEBYSHEV du premier ordre.
Donc la solution ço(s) prend la forme suivant :
--
1 N
ço(s) = (1-- s2 ) 2 E A
nT n(s) (1.13)
n=0
On substitue ço(s) dans l'équation
intégrale et en utilisant les relations suivantes :
1
|
1
71-
|
--
iT n(s)(1 -- s2) 2 dt U n > 0
s -- r 0, n = 0
-- 1
|
(1.14)
|
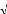
Où : Un (r) = sin((n +1) arccos(s)) / 1--
s2 désigne les polynômes de CHEBYSHEV de
second ordre. L'équation intégrale se transforme en
un système de N équations a N inconnues appelées
A1,......... ...., A
·
N
·
|
N Er
AniU n--1(rj)+H nfr )
|
g (r
|
), j =1,......, N . (1.15)
|
n=1
Les r j sont les points de collocations donnée
par :
|
r j
|
= cos (2 j --1)71-)
2N
|
,j =1,......, N . (1.16)
|
Avec n(rHestj) donnée par :
1 1
(r j) =1 f (1-- s2 ) 2
laL(rj , s)Tn(s)ds
71-
--1

(1.17)
Ces intégrales sont évaluées
numériquement en utilisant la formule d'intégration de
GAUSSCHEBYSHEV suivante :
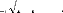
n
1 1 f (t)dtf (t k)
E
1t21
Tn (t k) = 0 (1.18)
Apres avoir obtenu les A. , il et facile d'évaluer le
facteur d'intensité des contraintes k3 aux pointes #177;
la et l'ouverture 8(r) le long des lèvres de la
fissure.
Les données du problème sont :
l0 = 1mm, h = 1mm, p = 1 100MPa,
'rc = 7 2 MPa.
--
Dans la phase cohésive, une zone cohésive
apparaît dés le début du chargement. Il est facile de
calculer 'ro. en supposons la connue, la loi
donnant 'ro. en fonction dela est k3
(la ) = 0,
en utilisant la linéarité du problème
élastique on a : k3 (la ) =
'roo.k3"(la)+ k3
(la) ou k3" (la) et
|
d'obtenir l'ouverture
|
[w
|
](la)
|
=
|
Sa
|
. Les quantités numériques calculées sont
représentées sur
|
37 4(la) sont respectivement le FIC du
problème sans forces cohésives et Too =1, et
le problème avec forces cohésives etToo = 0 .
L'équation k3 (la) = 0 donne T
=-ka(l a)
3 . Le calcul de la
k3 (la )
charge Too demande le calcul des FIC
k3oo (la) et k3 (la) . Les valeurs
calculées sont représentées sur la figure donnant la
relation entreToo et la (figure 1.21),
ainsi Too est une fonction strictement croissante de
la et tende vers Ta lorsque la tende
vers l'infini.
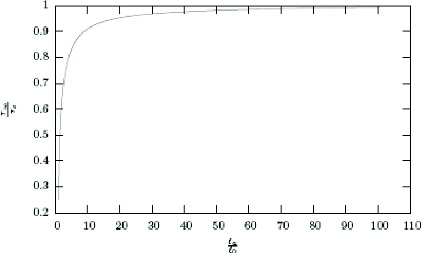
Figure 1.21 .Relation entre la charge appliqué et la
position de la zone cohésive dans
la phase cohésive.
La phase cohésive cesse lorsque l'ouverture en
x1 = #177;la dépasse la valeur critique
Sa. Pour déterminer la charge de rupture, pour la
longueur caractéristique Sa , la méthode
numérique utilisée est la suivante :
Pour la valeur test de la donné,
Too est obtenue en résolvant l'équation k3
= 0 avec la méthode
expliquée dans le paragraphe
précèdent, La valeur réelle de la et obtenu par
dichotomie afin
|
d'obtenir l'ouverture
|
[w
|
](la )
|
=
|
8a
|
. Ainsi on obtient finalement z8 en
fonction de la pour
|
un diagramme z,. - 8a (figure 1.22).
La charge de rupture est une fonction croissante de 8a .
On
|
note que la charge de rupture tend vers za
quand
|
8a tend vers l'infini. l0
|
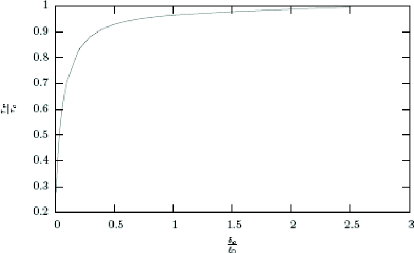
Figure 1.22. Dépendance de la charge de rupture et la
taille relative de défaut
initiale.
Pour prouver que z,. est vraiment la charge maximale
que le corps peut supporter tout en vérifiant les équations
d'équilibre et les critères de rupture, on impose la valeur de la
pointe non cohésive la , on calcule la valeur de la
chargez8 et de la pointe cohésive la en
résolvent le système d'équations non linéaires
(1.4). La méthode numérique utilisée est la suivante. Pour
la valeur test de la donnée, z8 est
obtenu en résolvant l'équation k3 = 0 avec la
méthode expliquée dans le paragraphe précèdent. La
valeur réelle de la et obtenu par dichotomie afin
charge limite de la structure fissuré. Les
résultats (figure 1.23) représentant la relation
entreô8 et la pour
äc de 0.1mm , la charge de rupture est de 0.71ô
,..
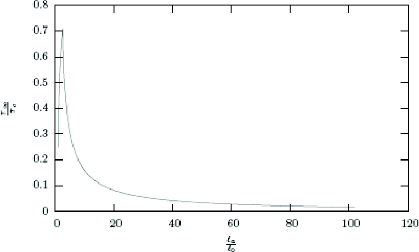
Figure 1.23. Relation entre la charge et la longueur de la
fissure pour äc = 0.1.
CHAPITRE 2
LE PROBLEME TRAITE
On considère une bande infinie SI = (--...,+.0)x (--h, h)
contenant un défaut de type fissure D
=[-l0,l0]x{0}de longueur 2l0 interne et
distant de h de la face supérieure et la face
inférieur de la bande. Le matériau constitutif de
la bande est élastique isotrope caractérisé par
un
module de cisaillement p . Les faces supérieurs et
inférieures sont soumises à une
contrainte de cisaillement anti-plan positive et uniforme
i-o. , augmentée a partir de 0. Les
lèvres de la fissure ne sont pas chargées (figure 2.1).
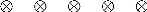
1-0.

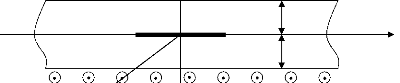
h
la h x1
-
la
x3
Figure 2.1. Géométrie de la bande avec les
chargements.
Pour le présent problème, la seule composante non
nulle du vecteur déplacement, et la composante dans la direction
x3 , cette composante est indépendante de x3 .i.e
:
u1 = u2 = 0, u3 = W(x1, x2 ) (2.1)
Donc, le champ de contrainte correspondant est donnée par
:
0
=
211 = 222 =
233 = 212
(2.2)
?W ?W
, p
=
2 13
p
?x
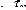
1 ?x2
2
23
Le champ de déplacement W et les deux composantes non nul
du champ de contrainte 213 et 223
doivent satisfaire le système d'équation suivant :

~ÄW = 0,
~ ?W
213 ,
?x1
~223 = 0, ~
~223 =
~ ~223 = 2
D
Ù
D
dans
D
W
Ù
=
dans
D
223
D
?x2
sur
(2.3)
sur
x2 = h
sur
x2 = -h
L'initiation et la propagation de la fissure dans le corps suit
le modèle de DUGDALEBARENBLATT est caractérisé par les
paramètres suivant Gc , 2c et
äc .
U
Introduisons les nouvelle fonction inconnues W, 2U
définis par :

.x2
x2
W(x1 )
W(x1, )
x
2
+
2 8
p
(2.4)
)
?e2
?W
2-23 (x1, x2 = p
(2.5)
?x2

U
(x1, ) =
x2
213
?x
1
2 = +.(e2?e3 + e3
Ou les termes non nul de2U sont
'Le13 ,'Z'23 défini par :
~
~~ ~ ~
~ ~
|
|
42
|
|
dans sur sur sur
|
II / D
D
=
x2 h
x2 = -h
|
(2.6)
|
,
0
=
A W
,
r .n = -r .n
-
,
r23
,
r23
|
Dans la décomposition (2.4), le terme
|
r x2
. est associé à la solution du problème de
la bonde
|
Il
non fissuré sollicité par un champ de contrainte
uniforme de cisaillement anti-plan. Les
quantités inconnus W,i-13
et 'Le2 3 correspond a la solution du problème de la
bande fissuré. On
note que ce problème consiste à déterminer
la réponse de problème de la bande fissuré lorsque
les
contraintes de cisaillement - ron sont appliquées
sur les lèvres de la fissure. Les faces
supérieures et inférieures de la bande sont libres
(figure 2.2).
x2

x3

-
la
la h x1
h
Figure 2.2. Géométrie de la bande avec les
chargements après la superposition.
,
Dans la suite on omet les symboles tildes, les champs W ,
rU soit notés respectivement
Pour des raisons de symétrie, on suppose que la fissure
se propage le long des axes x2 = 0 d'une façon
symétrique depuis les points (#177;l0,0) ainsi on note par F
la nouvelle fissure crée et par x2 = #177;la la position de
ses pointes, avec :
F = (-la ,-l0 ] x {0}U [l0 ,
la )x {0} (2.7)
L'évolution de la fissure suit la loi de
DUGDALE-BARENBLATT, en d'autre terme les pointes de la fissure (- la
,-l0 ) et (l0 , la) peuvent comporter deux
zones :
· La première zone, proche des pointes de la fissure
appelée la zone cohésive, et soumise a une force cohésive
de cisaillement constante d'intensité Tc .
· La seconde zone appelée non cohésive, et
proche de la fissure initiale sans forces cohésives.
Ces deux zones sont séparées par les pointes
x1 = #177;lc. Notons que, les valeurs de la
et
lc dépendent de la valeur de chargement
T.. sous l'hypothèse la = lc = l0
. Au début du chargement, on a les conditions initiales suivantes:
la = lc = l0 .
Dans le cas présent l'évolution de la
fissuration suit deux phases, la phase cohésive et la phase de
propagation. Les critères de l'initiation et la propagation de ces zones
sont étudiés dans les sections suivantes :
| 


