1.3.3 Modèle de DUGDALE régularisé
[19]:
|
L'étude consiste a montrer l'influence de l'effet
d'échelle .i.e du rapport
|
gc sur la l0
|
contrainte de rupture, pour des raisons de facilité de mis
en ouvre numérique on garde une dimension constante du défaut et
en fait varier l'ouverture critique gc .
Comme donnés du problème nous choisissons: L
=100(mm), l0 =3(mm).
Pour le matériau celles d'un polymère PMMA.
óc = 72MPa , E = 3000MPa , í = 0.36 . Le
saut critique de décohésion g0 = 0.00402(mm)
.
Les calculs sont fait numériquement par la
méthode des éléments finies pour les deux cas de fissure
pré existante et de la cavité circulaire, le domaine est
maillé par des éléments finis triangulaires a 3 noeuds
(pour des raisons de symétrie un quart du domaine est maillé,
figure 1.15) la ZCC est modélisé a l'aide
d'éléments d'interface quadrangulaires d'épaisseur
nulle.
Figure 1.15. Maillage d'un quart du domaine pour le cas du trou
et la fissure.
Comme énoncé précédemment,
l'évolution de la fissure commence par la phase élastique la
charge d'amorçage óa
(ó8 a partir de laquelle l'ouverture dans la ZCC en
points ( #177; la ,0)
atteint le saut critique g0 ), est obtenu en
effectuant un calcul purement élastique est égale a
6.55MPa pour la fissure et a 9.36MPa pour le trou.
Au-delà de óa une zone
cohésive apparaît c'est la phase d'amorçage. Les
résultats de la
phase d'amorçage données pour le trou et la fissure
sont sur la (figure 1.16).

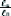
Figure 1.16. Relation entre la charge appliquée et la
position de la zone cohésive
dans la phase cohésive.
On remarque que la charge dans cette phase est une fonction
croissante de la longueur de la zone cohésive. En outre on observe que
les courbes sont identiques, on peut conclure que la sensibilité de la
phase d'amorçage à la forme du défaut est faible.
La charge de rupture ó est la contrainte
appliqué correspondant a des ouvertures de la fissure [[un
(#177;l 0)]]= ga et [[un (#177;l
a)]]= g0 . Cette charge est déterminée
pour une longueur caractéristique et pour plusieurs valeurs de la
longueur caractéristique ga (g0
reste fixe). Les valeurs numérique calculées pour la fissure et
le trou sont représentées dans un diagramme
a, -- 8c (figure 1.17), comme
attendu la charge de rupture est une fonction croissante de
8c , on observe que la charge de rupture n'atteint jamais la
valeur ac quelque soit 8c ceci est du
aux dimensions finis de la plaque.
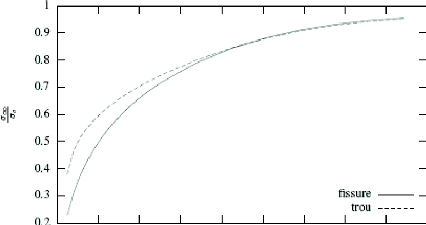
Figure 1.17. Relation entre la charge de rupture et la taille
relative de la longueur
caractéristique 8c .
En effet, en utilisant un raisonnement
élémentaire de calcul à la rupture, il est facile de
voir
~/
que la plaque trouée ne peut pas supporter une charge plus
grande que 1-- 0 L ac qui
correspond à la charge d'équilibre de la plaque
lorsque la zone cohésive occupe toute la largeur de la plaque. Compte
tenu des valeurs numériques choisies, la charge de rupture ne peut donc
dépasser 0.97ac . Notons enfin que si l'on faisait
tendre la longueur du défaut vers 0 ou la largeur de la plaque vers
l'infini, alors la charge de rupture tendrait vers ac.
Il reste à prouver que la charge a, est
réellement la charge maximale que la structure peut supporter. Peur ce
faire, on fixe la valeur de la pointe cohésive /c et on
calcule la valeur de la charge a_et de la pointe cohésive
/a. Nous avons représenté sur la (figure 1.18) la
relation entre a_ et /a pour une valeur de
8c égale à 0.00804 mm respectivement pour le trou
et la
fissure. Il s'avère que ac. est une
fonction décroissante de la, ceci prouve que
ar est une charge
limite et par conséquent la charge de rupture de la
structure. Les charges de rupture sont 0.356c pour le trou
et 0.16sc pour la fissure.
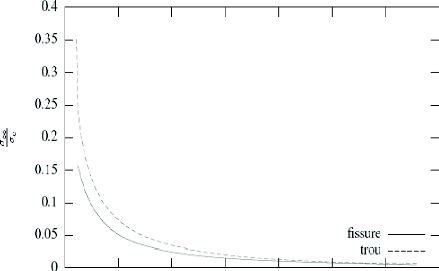

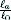
Figure 1.18. Relation entre la charge appliquée et la
position de la zone cohésive
dans la phase de propagation.
| 


