1.3 Synthèse des travaux de FERDJANI et al :
1.3.1 Cas d'une plaque pré fissurée ou
trouée :
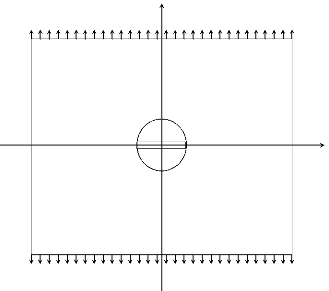
La structure consiste en une plaque carré de dimension
SI = (-L,+L) sollicitée en traction et contenant un défaut
centré D et soumis, sur les faces supérieure x2 = +L
et inférieure x2 = -L à une traction uniforme
d'intensité a8 croissante depuis 0. Le défaut
est soit une fissure préexistante perpendiculaire à l'axe de
traction et de longueur 2/0, soit un trou circulaire de rayon
/0 (figure 1.8). L'étude s'effectue dans le cadre des
déformations planes
pour le modèle de DUGDALE, et de contraintes planes pour
le modèle de DUGDALE régularisé, le matériau est
linéairement élastique, homogène et isotrope.
-
L
L
x1
x2
a_
-
Io
Io
a_
Figure 1.8. Géométrie de la plaque contenant le
défaut initial centré
1.3.2 Modèle de DUGDALE [19] :
L'étude consiste à montrer l'influence de l'effet
d'échelle .i.e. du rapport

Sc sur la
Io
contrainte de rupture, pour des facilités de mise en ouvre
numérique on garde une dimension constante du défaut et en fait
varier l'ouverture critique Sc .
· Cas d'une fissure préexistante :
Le défaut initial est une fissure non cohésive de
longueur 2I0 (figure 1.8) La plaque est
supposée infinie. Pour cette étude, on se servira
de la solution donnée par BUI (1978) [4] pour
une fissure
cohésive de longueur 2Ia placée dans un milieu infini,
soumise à l'infinie à une
traction simple d'intensité a_ dans la
direction 2 et ayant a ces extrémités x1 =
#177;Ic une zone
cohésive dont les pointes sont en
x1 = #177;Ia. Les lèvres des zones
cohésives sont soumises à
une contrainte normale de traction d'intensité
constante aa. On peut considérer que
l'approximation faite est d'autant meilleure que la taille du
défaut est plus petite devant la taille du domaine. Le problème
se réduit donc a un problème d'élasticité plane
posé sur un domaine infini fissuré avec une distribution
donnée de forces. Il se résout classiquement à l'aide de
potentiel complexe suivant les techniques développées dans
MUSKHELISHVILI (1963) [36].
Dans la phase d'amorçage, lorsque l0 =
la les contraintes sont singulières dans la réponse
élastique de la structure dés la mise en charge.
Ceci mène à dire que la charge d'amorçage est
nulle
aa = 0 . Une zone cohésive de longueur la se
développe dés la mise en charge. Le
graphe représentant la charge appliqué
a8 en fonction de la position de la pointe d'amorçage
la (figure 1.9) montre que la charge croit de 0 a
aa quand la zone cohésive croit de l0a
l'infini. Ceci est valable tant que l'ouverture en x1 =
la n'atteint pas la valeur critique äa la
charge appliquée correspondante est appelé charge de rupture
a,..
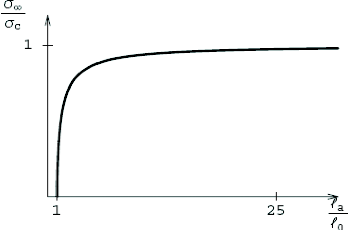
Figure 1.9. Relation entre la charge appliquée et la
position de la zone
cohésive lors de la phase d'amorçage.
La phase de propagation commence lorsque l'ouverture en
lc atteint le saut critique 8c .
Dans ce cas, on doit diminuer la charge si l'on veut que la
propagation de la fissure soit stable. Ceci signifie que la charge de
rupture a,. est en fait la charge limite que peut supporter la
structure.
Dans un diagramme a_ -- la (figure 1.10) est
représenté l'évolution de la fissuration avec
la charge pour une valeur donnée du
8c . On notera que la longueur interne
8c n'intervient que
dans la phase de propagation (et donc évidement dans la
charge de rupture) la charge de rupture valent dans ce cas a,. =
0.76.ac.
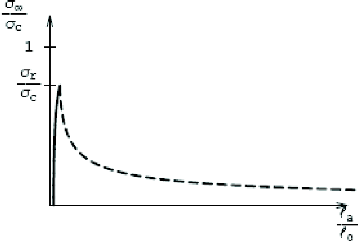
Figure 1.10. Relation entre la charge appliquée et la
position de la zone cohésive :
En trait plain, lors de la phase
d'amorçage, en pointillés lors de la phase de
propagation.
La charge de rupture dépend de façon essentielle
du rapport entre la longueur l0 du défaut initial et la
longueur caractéristique 2c (qui est proportionnelle
à 8c) du matériau, ceci est
représenté dans un diagramme donnant la dépendance de la
charge de rupture par rapport la taille relative de la fissure (figure 1.11),
plus la taille relative du défaut est petite et plus la charge de
rupture se rapproche de la contrainte critique ac du
matériau, et ce bien qu'il y'ait amorçage d'une nouvelle fissure
dès la mise en charge. On peut donc conclure qu'avec la loi
de DUGDALE, la plaque est pratiquement insensible aux petits
défauts initiaux de petite taille de type fissure.
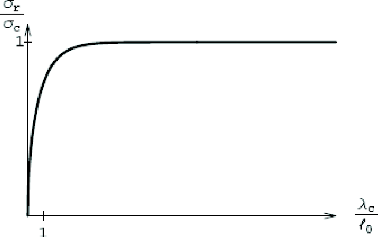
Figure 1.11. Dépendance de la charge de rupture avec la
taille relative de la
fissure initiale.
· Cas d'une cavité circulaire :
Le défaut initial est une cavité circulaire de
rayon 10 centré en (0,0) (figure 1.8) les données du
problème sont :
La plaque est de dimensions 20 × 20mm .
Le rayon du trou est de longueur 10 = 1mm .
Le calcul est effectué avec la méthode des
éléments finis.
Le domaine est maillé avec des éléments
triangulaires a 3 noeuds (pour des raisons de symétrie et de conditions
aux limites seul un quart du domaine et maillé), (figure 1.12).

Figure 1.12. Géométrie de la plaque trouée
avec les zones cohésive et non
cohésives.
Pour les données matériau, on choisit celle d'un
polymère PMMA : ac = 72(MPa),E =
3000(MPa),í = 0.36.
Un calcul purement élastique mène à
déterminer la charge d'amorçage aa (la
charge a8 a partir de laquelle la
plus grande contrainte principale atteint la valeur critique
ac en un point de la structure). Pour des raisons de
symétrie et de conditions aux limites la concentration des contraintes a
lieu au bord du trou aux points (#177;l0,0) si la plaque
été de dimension infinie, la contrainte an en
ces points serait exactement égale a 3a8 et la
charge d'amorçage a ac /3 = 24MPa. En raison des
dimension finie de la plaque et des approximations numérique, la charge
d'amorçage calculée aa est égale a
22.2MPa.
Dans la phase de propagation, une zone cohésive
apparaît et s'étend si l'on augmente la charge au-delà
de aa . La longueur de cette zone correspond a un facteur
d'intensité de contrainte nulle 1(1(la ) = 0 .
D'un point de vue numérique, cela nécessiterait d'itérer
sur la valeur de la , la stratégie numérique
adoptée est la suivante :
1. On itère sur la valeur de la en partant de
la valeur obtenu au pas précédent.
2. On calcule l'ouverture [[un ]]au noeud du maillage
le plus proche de la pointe /a.
3. Si cette ouverture est positive, alors on incrémente
/a et on arrête les itérations quand elle devient
négative.
La charge de rupture est déterminée pour une
langueur ëc donnée, suivant un
procédé basé sur une méthode itérative, les
valeurs numériques calculées sont représentées dans
un diagramme ó,. - ëc (figure
1.13).
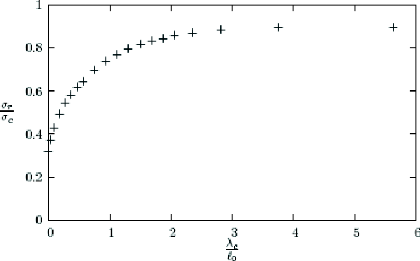
Figure 1.13. Dépendance de la charge de rupture avec la
taille relative de la
fissure.
On remarque que la charge de rupture est une fonction
croissante de ëc , mais elle n'atteint jamais la
valeur óc quelque soit la valeur de
ëc . Ceci est dû au caractère fini des
dimensions de la plaque. En effet, en utilisant un raisonnement
élémentaire de calcul à la rupture, il est facile de voire
que la plaque trouée ne peut pas supporter une charge plus grande que
/
(1- ° L ).ó qui correspond à la
charge d'équilibre de la plaque lorsque la zone cohésive
c
occupe toute la largeur. Compte tenu des valeurs
numériques choisies, la charge de rupture ne
peut donc dépasser 0.9.aa . On voit
que cette valeur est pratiquement atteinte lorsque ëa
= 3l0.
Notons enfin que si l'on faisait tendre la longueur du
défaut vers 0 ou la largeur de la plaque vers l'infini, alors la charge
de rupture tendrait vers aa .
Un calcul de la phase de propagation effectué pour une
position donné de la zone cohésive a permis de vérifier le
résultat précédent concernant la charge limite, suivant un
procédé itératif de détermination de la charge
a_ équilibrant la structure fissurée avec la pointe de la
zone cohésive en la. Ceci a permet
d'obtenir a_ en fonction de la pour un
ëa donné. Lorsque la = l0 on
a évidemment a_ = a,.. Il s'avère que dans tout
les tests effectués a_ est une fonction décroissante de
la , ce qui prouve bien que a,. est une charge limite et
donc la charge
de la structure trouée. Les résultats obtenu pour
cette phase sont présenté sur un diagramme
donnant la relation
entre a_ et la pour une valeur de
äa = 0.01mm (figure 1.14), la charge de
rupture valant 0.450aa .
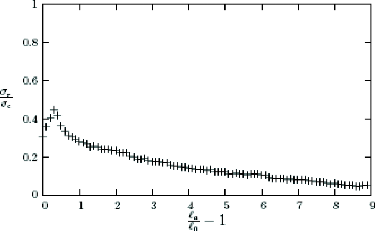
Figure 1.14. Relation entre la charge et la longueur de la
fissure.
| 


