1.2.3 Modèle de NEEDLEMAN [38] :
Ce modèle décrit l'évolution des forces
cohésives normale a,, et tangentielle a, en
fonction des composantes normale et tangentielle du saut de
déplacement 8,, et 8, . On
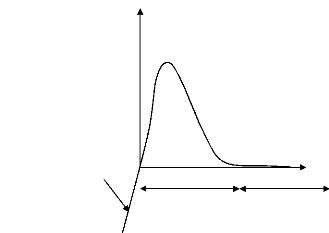
représente sur la Figure 1.6, l'évolution de la
force normale en fonction du saut normal quand le saut tangent est nul.
8c
8,,
a,,
ac
Pénalisation du contact
Zone cohésive Rupture
Figure 1.6. Loi d'interface de NEEDLEMAN dans la direction
normale.
Les forces dérivent d'un potentiel y/ :
a y/
cr --
,, a8,,
,t
a y/
.
cr = a8
t
Ce dernier est choisi comme une fonction polynomiale faisant
intervenir les paramètres ac contrainte critique du
matériau en ouverture, 8c saut critique
au-delà duquel l'interface
entre les lèvres de fissure devient nulle ainsi que la
part de résistance au glissement par
rapport à la
résistance normale. On note que lorsque 8,, < 0 la valeur de
la contrainte normale
dérive du potentiel joue le rôle d'une
pénalisation afin de tenir compte de la condition de non
interpénétration des lèvres de la fissure. Aucune autre
hypothèse n'intervient pour prendre en compte cette condition. Notons
que ce modèle fut repris et modifié par de nombreux auteurs.
Citons par exemple RICE et WANG [39] qui ont proposé une expression
exponentielle du potentiel. La différence avec le modèle
précédent tient au fait que la force tend asymptotiquement vers
zéro quand le saut de déplacement augmente. Ce modèle ne
fait donc pas intervenir le paramètre 8c .
1.2.4 Modèle de TVERGAARD [43] :
Ce modèle reprend le modèle de NEEDLEMAN de 1987
[38] et introduit une notion d'irréversibilité du comportement :
la décharge s'effectue linéairement, ainsi qu'un frottement de
COULOMB post décohésion. On représente sur la Figure 1.7
l'allure de la force tangentielle en fonction du saut tangentiel lorsque le
saut normal est nul.
Notons que le modèle formulé initialement par
l'auteur s'appuie sur un indicateur de décohésion variant de
zéro à un, faisant intervenir le saut normé par le saut
critique, et qui fait office de variable d'endommagement dont dépendent
les forces d'interaction.
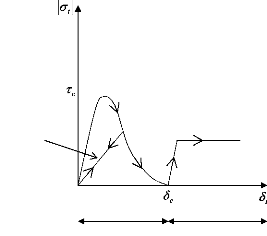
Frottement
0
Zone cohésive
Décharge
Figure 1.7. Evolution de la force tangentielle en fonction du
saut tangent.
D'autres modèles ont été
développés en s'inspirant de celui-ci. Par exemple, CHABOCHE et
al (1997) [6], pour modéliser la décohésion interfaciale
dans les composites à matrice métallique, proposent d'activer le
frottement de COULOMB dés le début de la
décohésion. Citons par ailleurs CHABOCHE et al qui reprennent ce
dernier modèle et introduisent une régularisation visqueuse afin
de lisser les instabilités intervenant dans l'ouverture brutale de
fissure. La réponse dépend alors de la vitesse du chargement.
Cette technique permet de remédier aux problèmes
numériques liés à un saut de solution important difficile
à capter avec des méthodes de type NEWTON. Cela permet d'avoir
une réponse globale continue à tous les
niveaux de chargement mais cette technique modifie les
équations de comportement de l'interface.
Notons par ailleurs que ces lois peuvent être
utilisées soit pour décrire le comportement d'une interface :
séparation de deux parties d'un solide comme la propagation de fissure
(objet d'épaisseur nulle) soit pour représenter le comportement
d'une interphase entre deux matériaux (objet volumique de faible
épaisseur) pouvant représenter une colle. A ce sujet SUQUET [42]
et MICHEL et al [37] ont travaillé sur la modélisation
d'interphase dans les composites à matrice métallique. Ce type de
modèle pose des questions de convergence mathématique du
modèle d'interphase vers le modèle d'interface.
| 


