Etude de l'influence des efferts d'echelle dans le modele de Dugdale

1.2 Lois d'interface des modèles de force cohésive [33]:

On appelle loi d'interface une relation entre le déplacement relatif et la force d'interface entre les lèvres d'une fissure. Dans cette partie nous présenterons quelques unes d'entre elles basées sur la notion de force cohésive. Cette dernière s'appuie sur des observations expérimentales en pointe de fissure telles que l'apparition de micro fissures, la croissance de cavité ou le développement de zones de plastification. Cela correspond à une zone de transition entre le milieu sain et une vraie fissure (figure 1.1).

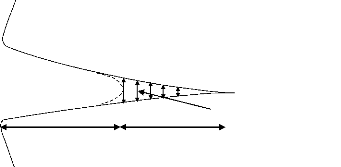
Interaction (forces cohésives)

Fissure Zone cohésive

Figure 1.1 : Schéma de la fissure et de la zone cohésive.

Les premiers modèles furent introduits par DUGDALE et BARENBLATT au début des années soixante. Prenant acte du fait que les contraintes infinies en pointe de fissure, prédites par le modèle élastique (IRWIN [31]), n'ont pas de signification physique, ces derniers ont émis l'hypothèse de l'existence d'une «zone cohésive» (Fracture Process zone dans la littérature) dans laquelle des forces s'exercent entre les futures lèvres de la fissure. Dans les années soixante-dix HILLERBORG et al [30], ont introduit le concept d'énergie de rupture dans les modèles de force cohésive et proposé quelques relations de comportement entre la traction et le saut de déplacement pour le béton. De nombreux modèles ont été développés depuis, citons en quelques uns :

1.2.1 Modèle de DUGDALE [33]:

Ce modèle décrit l'évolution des forces de traction a_a en fonction du saut de déplacement normale 8_a . Le saut reste nul tant que la force n'atteint pas une valeur critique cr_a puis le comportement utilisé est celui d'un solide rigide parfait jusqu'à un seuil d'ouverture 8_a au- delà duquel l'interaction des lèvres devient nulle (Figure 1.2 et 1.3).

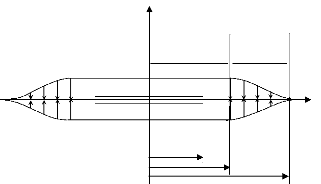
Zone
cohésive

Zone non
cohésive

cf_a

x₁

l_a

l₀

l_a

x₂

Figure 1.2. Schématisation du modèle de Dugdale-Barenblatt

cr aa

17

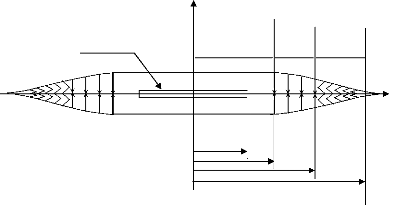
Fissure initiale

cr_a

Zone non cohésive

l₀

l_a

Zone
cohésive

l_a

Zone
cohésive
Continuum

x₁

0 8_a 8

Figure 1.3 . Loi d'interface de DUGDALE dans la direction normale.

1.2.2 Modèle de DUGDALE régularisé [20]:

C'est une combinaison entre le modèle des zones cohésives continuums (ZCC) (Xie [45]) et le modèle de DUGDALE (figure 1.4 et 1.5).

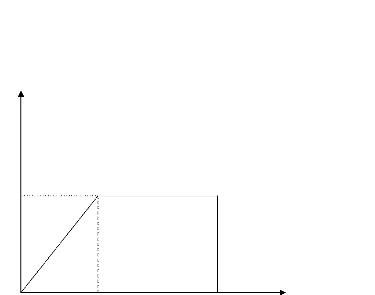
a,,

a_c

18

8₀ 8c nu ,,II

Figure 1.5. Loi de comportement dans le modèle de DUGDALE régularisé.

a_c désigne la contrainte critique du matériau, 8_c désigne la longueur caractéristique du modèle, et 8₀ désigne le saut critique de décohésion. La fissure est donc divisée en trois

zones représentées sur la figure 1.4.

La loi de comportement, donnant la relation entre les forces cohésives et l'ouverture des lèvres de la fissure, en supposant que l'ouverture se fait en mode I pur, est représentée sur la figure 1.5.

⁸,, Désigne la discontinuité du déplacement normale, _a,, désigne la contrainte normale

d'interaction entre les lèvres de la fissure.