INTRODUCTION
L'objet de la mécanique de la rupture est de
déterminer l'évolution d'une ou plusieurs fissures dans une
structure en fonction du chargement auquel elle est soumise. Le cadre de la
mécanique de la rupture fragile se limite à l'étude de la
fissuration des milieux continus supposés élastiques. Cette
hypothèse, bien qu'idéaliste, reste le cadre d'étude de
nombreux chercheurs et ingénieurs préoccupés de
sûretés concernant la propagation de défauts dans les
structures en service. C'est le cadre des travaux de LAVERNE [33].
Dans ce formalisme, les principaux résultats ont
été obtenus à partir de la théorie de GRIFFITH. Ce
dernier associe à toute fissure une énergie de surface
proportionnelle à sa longueur. Il postule qu'il y aura propagation et
donc augmentation de l'énergie de surface si cette dernière est
parfaitement compensée par la restitution de l'énergie
élastique causée par l'avancée de la fissure. Dans le cas
de problèmes quasi-statiques, ce critère peut se formuler en
terme de taux de restitution d'énergie élastique usuellement
noté G. Ce dernier correspond à la variation d'énergie
potentielle lors d'un accroissement infinitésimal de la fissure. Le
critère de GRIFFITH stipule alors qu'il n'y aura pas propagation tant
que :
G < Gc
Ou Gc désigne le taux de restitution
d'énergie critique et correspond à la ténacité du
matériau.
Bien qu'elle connaisse encore un vrai succès, cette
théorie renferme des insuffisances notoires.
- La première concerne l'initiation de la fissuration,
la théorie de GRIFFITH est incapable de rendre compte de
l'amorçage de fissures, sauf dans des cas très particuliers ou la
structure possède des singularités fortes. En effet, prenons
l'exemple d'un milieu bidimensionnel contenant une fissure rectiligne Z,
sollicitée en mode I, et supposons l'absence de singularités dans
le problème d'élasticité initiale. Le critère de
10
GRIFFITH prévoit que la fissure se propage pour un
chargement en 1 / . Si / tend
vers zéro, on en déduit que pour un milieu sain
la fissure ne pourra pas s'amorcer sous un chargement fini.
- La seconde lacune porte sur son incapacité à
prédire seule le trajet spatial des fissures. Pour un milieu
bidimensionnel, le critère ne prend en compte que la longueur de fissure
or l'évolution spatiale nécessite une seconde information qui
correspond à un critère de branchement.
- Enfin, une troisième lacune concerne le trajet
temporel de la fissure, seules les propagations progressives sont
traitées de façon satisfaisante. En effet des situations ou
l'inégalité du critère est violée peuvent survenir.
Celles-ci correspondent au cas de figure ou l'excès de restitution
d'énergie élastique conduit à l'apparition
d'énergie critique. La propagation est alors considérée
comme brutale.
On peut résumer ces trois points en disant que le
problème majeur de la théorie de GRIFFITH est de ne pas laisser
assez de souplesse à l'évolution spatio-temporelle des fissures.
De nombreux aménagements tentent d'y remédier proposant des
ingrédients spécifiques à chacun des problèmes
[33].
Le modèle de rupture de DUGDALE- BARENBLATT ou de
façon plus générale les modèles de forces
cohésives présentent l'avantage [33], sur le modèle de
GRIFFITH, de rendre compte de l'amorçage de fissure dans une structure
saine en termes d'un critère en contraintes, cf. par exemple DEL PIERO
(1999) [12], DEL PIERO et al. (2001) [13], CHARLOTTE et al. (2000) [7] ou
LAVERNE et al (2004) [34]. De façon générale, les
modèles de force cohésifs sont de plus en plus employés et
il est donc nécessaire de connaitre de mieux en mieux leurs
propriétés pour pouvoir les utiliser à bon escient. En
particulier les effets d'échelle qui les accompagnent du fait de la
présence d'une longueur caractéristique sont mal connus. Il ne
s'agit évidement pas ici de valider le modèle de DUGDALE, ni de
voir pour quel type de matériau il peut être utilisé, mais
de voir s'il est assez robuste pour que, grâce aux effets
d'échelle qu'il induit, la réponse des structures ne soit pas
sensible à des défauts de petite taille. L'étude sera donc
essentiellement théorique et numérique. De plus, nous
envisagerons seulement des zones cohésives linéiques [19].
0
G c

Sc [[un]]
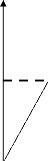
Densités d'énergie de surface dans les
modèles de Dugdale et Griffith
Ces modèles, formulés en termes
énergétiques, consistent à supposer que la densité
d'énergie de surface 0 dépend de façon non
triviale du saut de déplacement [[un ]],
contrairement au modèle de GRIFFITH ou elle est constante.
Ainsi dans le modèle de DUGDALE, en supposant que l'ouverture se fait en
mode I pur, elle s'écrit :
=Sc
=Sc
0 = G
c .
(nu n11) I [[uSnli si [[u nli
c rr Ti
Gc si L'uni]

[[un ]]désigne le saut du déplacement
normal, G c représente le taux de restitution
d'énergie critique de la théorie de GRIFFITH, alors que
Sc est une longueur interne caractéristique des
modèles de forces cohésives. Le rapport G c
Sc a la dimension d'une contrainte et représente la
contrainte critique du matériau :
=
Gc
a .
c
Sc
En termes de forces cohésives, la contrainte normale
an d'interaction entre les lèvres de la
fissure vaut
donc ac tant que [[un ]] <
Sc et s'annule dés que [[un ]] >
Sc . En pratique, les lèvres
des fissures sont donc
divisées en deux zones : une zones dite cohésive dans laquelle
les
forces cohésives ne sont pas nulles et une zone dite
non cohésive dans laquelle il n'y a plus de force cohésive. La
zone cohésive se situe près de la pointe, là ou
l'ouverture ne dépasse pas le seuil critique äc
[19].
Le fait que acjoue le rôle de
contrainte critique se vérifie dans l'étude d'une barre en
traction simple. En raisonnant comme DEL PIERO (1999) [12] ou
CHARLOTTE et al.
(2000) [7] à partir d'un principe de minimisation
d'énergie, on montre que la réponse
élastique (le champ
de déplacement est de la forme u(x) = axlE,E étant le
module d'Young)
cesse d'être un minimum relatif de l'énergie
(totale) de la barre lorsque la contrainte
appliquée a
dépasse la contrainte critique ac . La
conséquence directe de cette présence d'une
contrainte critique dans le modèle est qu'une structure
donnée ne pourra pas supporter n'importe quel niveau de chargement
conformément aux résultats classiques des théories de
calcul à la rupture ou d'analyse limite, cf. SALENCON (1983) [40].
Cependant il y a lieu de distinguer les charges limites élastiques, i.e.
les charges à partir desquelles doit développer une fissuration,
des charges limites proprement dites, i.e. des charges maximales que peut
supporter la structure même en se fissurant. Dans la suite nous
désignons les premières comme charges d'amorçage et les
secondes comme charges de rupture [19].
Rappelons tout d'abord ce qu'il en est de la charge
d'amorçage dans le cas du modèle de GRIFFITH. Notons que seuls
les défauts du type fissure, i.e. les défauts présentant
une
singularité « forte » en r pour le champ des
déplacements, sont susceptibles de se propager.
Les cavités,
les entailles et autres défauts non assez « pointus »
induisent une singularité trop
faible pour donner un taux de
restitution d'énergie non nul. Pour une fissure de petite taille 1
et de normale n, placée en un point x où les
contraintes normales en l'absence du défaut
seraient d'amplitude a, le taux de restitution
d'énergie est de l'ordre de a21. Il tend donc
vers
0 lorsque 1tend vers 0. Donc, dans la théorie de GRIFFITH ou les
fissures ne se propagent que
si le taux de restitution d'énergie
atteint la valeur critique Gc, les défauts de petite taille
sont
inoffensifs. C'est évidement un atout pour ce
modèle. Mais en contrepartie, le modèle de GRIFFITH est trop
conservatif puisqu'il ne sait pas rendre compte de l'amorçage de
fissures en dehors de points de fortes singularités, cf. FRANCFORT et
al. (1998) [25].
Si l'on abandonne le modèle de GRIFFITH au profit du
modèle de DUGDALE, le critère de propagation d'un défaut
ou d'amorçage de fissure ne se formule plus en termes du taux de
restitution d'énergie critique Gc, mais en termes de la
contrainte critique ac, cf.
CHARLOTTE et al. (2000) [7] et LAVERNE et al. (2004) [34]. Ce
faisant, on pourrait a
priori s'attendre à ce que la forme des défauts
joue un rôle essentiel et que ceux favorisant les concentrations de
contraintes s'avèrent plus nocifs. En particulier les fissures,
défauts qui induisent des singularités, devraient être
sensiblement plus défavorables que les cavités circulaires,
défauts qui par leur forme «parfaite» sont ceux qui engendrent
le moins de concentration. Ceci se révèle vrai pour la charge
d'amorçage, mais faux pour la charge limite. En effet, il est clair que
la charge d'amorçage est très sensible à la forme du
défaut puisqu'elle est directement liée aux concentrations des
contraintes induites par le défaut sur la réponse
élastique. Ainsi, dans le cas d'une fissure préexistante, du fait
de la présence d'une singularité de contraintes en pointe de
fissure, la charge d'amorçage est nulle, de nouvelles
discontinuités apparaissent dès la mise en charge. Par contre,
dans le cas d'un trou circulaire dans une plaque, la concentration de
contraintes est finie et donc la charge d'amorçage n'est pas nulle.
Nous verrons par contre que la charge de rupture, elle, est
beaucoup moins sensible à la forme du défaut qu'à sa
taille. En particulier, du fait de la présence de la longueur
caractéristique êc dans le modèle de
DUGDALE-BARENBLATT, les effets d'échelle sont
importants. La charge de rupture dépend de façon
essentielle du rapport entre la taille du
défaut et la longueur
caractéristique êc . Un résultat majeur serait
de montrer que, quelle que
soit la forme du défaut, la charge de rupture tend vers
la contrainte critique ac lorsque la taille
du défaut tend vers 0, à longueur
caractéristique fixée (ou de façon équivalente,
lorsque la
longueur caractéristique êc tend vers
l'infini, a taille du défaut fixée). Ceci signifierait qu'avec
le modèle de DUGDALE-BARENBLATT, les structures sont
insensibles aux petits défauts et se comportent comme des structures
saines, et ce bien qu'elles développent des zones d'amorçage
avant rupture [19].
Ce résultat a été obtenue par FERDJANI et
al [19], [20] pour une plaque contenant une fissure droite ou une cavité
circulaire soumise a une traction simple est pour les modèles de DUGDALE
et DUGDALE régularisés, et pour un milieu semi-infini contenant
une fissure droite [21] soumise à un cisaillement anti-plan, pour le
modèle de DUGDALE.
Dans le but de généraliser le résultat
obtenu, on propose d'étudier le problème antiplan d'une bande
infinie isotrope contenant une fissure cohésive parallèle
à la face supérieure de la bande et localisée au milieu.
Le modèles de DUGDALE-BARENBLATT (DUGDALE, 1960 [15]) est utilisé
pour modéliser l'interaction entre les lèvres de la fissure. En
utilisant les transformations de fourrier, les équations
d'élasticité sont converties analytiquement en une
équation intégrale singulière. A cause de la
présence de saut des discontinuités dans la distribution du
chargement le long des lèvres de la fissure, les méthodes
standard de
résolution de l'équation intégrale
singulière obtenu, ne sont pas appropriées. On utilise la
méthode proposée par (IOAKIMIDIS, 1980 [32]) pour traiter ce type
de chargement.
Ce mémoire est organisée comme suit, le premier
chapitre est consacré a la recherche bibliographique et contient une
présentation générale des modèles de forces
cohésives, suivi d'une présentation des travaux de FERDJANI et
al. Le chapitre 2 contient la présentation du problème
traité. Le chapitre 3 est consacré à
l'établissement de l'équation intégrale puis à la
résolution. Le chapitre 5 est consacré à l'exposé
des résultats des calculs. Enfin, une conclusion
générale.
CHAPITRE 1
ETUDE BIBLOGRAPHIQUE
1.1 Introduction :
Nous commençons par présenter une synthèse
des différents modèles de forces cohésives
présentes dans la littérature.
| 


