4.7 Conclusion :
))
(cos(
(cos( Dans le chapitre suivant nous allons présenter
les résultats du problème de la bande fissuré relativement
aux phases propagation et rupture pour plusieurs valeur de l'épaisseur h
de la bande, ainsi que les résultats du problème du milieu infini
fissuré. Nous allons voir que lorsque on augmente l'épaisseur les
résultat tendent vers s'eux du problème de milieu infini
fissuré.
CHAPITRE 5
PRESENTATION DES RESULTATS
5.1 Introduction :
Nous présentons dans ce chapitre, la méthode
numérique utilisée pour chaque phase. Nous présentons
également les résultats obtenus pour plusieurs valeurs de
l'épaisseur h données ainsi que les résultats pour le
problème du milieu infini fissuré pour faire une confrontation
des résultats, les caractéristiques mécanique et
géométriques du problème ont été
fixées aux valeurs suivantes :
l0 = 1mm, h =1mm, u =1100 MPa ,
rc= 72MPa (5.1)
5.2 La phase cohésive :
La zone cohésive apparaît et se développe
dés que ro. >0 . Le critère gouvernant la
propagation de la pointe de la fissure la est k3 = 0.
C'est une équation implicite relient ro. et la .
D'un point de vue pratique, il est facile de calculer ro.
en supposons la connue.
Effectivement, en utilisant la linéarité de
problème élastique, le Facteur d'intensité de contrainte
k3 (la) est donné par la formule suivante :
k3 (la) = r o.k ç
(la) + 4 (la) (5.2)
Ou k3oo (la) et k3(la
) sont respectivement le FIC de problème sans forces cohésives et
avec Too=1, et le problème avec forces
cohésives et Too = 0 . L'équation k3
(la) = 0 donne :
c
k3 l
Too = ( a) (5.3)
k7(la)
Spécifiquement, pour la valeur donné de
la on détermine la charge Too avec la
formule (5.3), les Facteurs d'intensités des contraintes
k3oo(la ) et k3 (la) sont
calculés avec la formule (4.32) avec lc =l0. Les
valeurs calculées sont représentées sur un diagramme
Too - la (figure 5.1). Pour plusieurs valeurs de
l'épaisseur h on vois ainsi que Too est une fonction
strictement croissante de la et qui tend vers Tc
quandla tends vers l'infini.
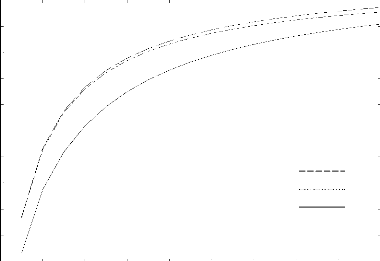
h inf
h= 10
h= 01
|
0.95 0.9 0.85 0.8 0.75
Too
Tc 0.7
0.65 0.6 0.55 0.5 0.45
|
1 2 3 4 5L 6 7 8 9 10
La
L0
5.3 La charge de rupture :
La phase cohésive cesse lorsque l'ouverture aux points
x1 = #177;1a dépasse la valeur critique
8a . Pour déterminer la charge de rupture pour la
longueur caractéristique 8a donnée, la
méthode numérique utilisée est la suivante :
)
=
8a
. Les
Pour la valeur test de 1a , T8
est obtenu par dichotomie en considérant [[4]](10
quantités numériques calculées sont
présentées sur un diagramme T,.-8a
(figure 5.2).
Comme attendu, pour plusieurs valeurs de l'épaisseur h la
charge de rupture et une
fonction croissante de 8a . On note que la
charge de rupture tend vers Ta lorsque
8a tend vers
10

|
T,.
|
1 0.9 0.8 0.7
|
|
|
|
Ta
|
0.6 0.5 0.4
0.3 0.2
|
l'infini.
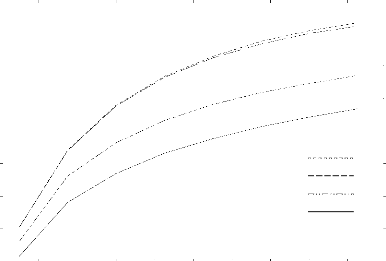
h=0.1
h inf
h= 10
h= 01
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
8a
10
Figure 5.2. Dépendance de la charge de rupture avec la
taille relative de la fissure initiale.
5.4 Phase de propagation :
la valeur de la pointe non cohésive la et on
calcule la valeur de la charge ô8 et celle de la
pointe cohésive la en résolvant le système
d'équation non linéaire suivant :
|
k3
|
(#177;la)
|
=
|
0,
|
[[wl(
|
#177;la)
|
=
|
8a
|
(5.4)
|
La méthode numérique utilisée est la
suivante. Pour une valeur test de la donnée,
ô8 est obtenu en résolvant l'équation
k3 = 0 avec la méthode expliquée ci-dessus. La bonne
valeur de la est obtenue par dichotomie de telle sorte que
=
.
8a
[[wl(
#177;la)
Nous présentons sur la figure 5.3 pour plusieurs valeurs
de l'épaisseur h l'évolution de la charge appliquée
ô8 en fonction de la pointe la.
|
0.9
0.8
0.7
0.6
ô8 0.5
ôa
0.4
0.3
0.2
0.1
0
|
Il s'avère qu'après la phase cohésive
ô8 est une fonction décroissante de la,
ceci prouve que ô, est une charge limite et donc la charge de
rupture de la bande fissuré, pour 8a ? 0.1 , la
charge de rupture est égale à0.8ôa .

h= 0.1
h inf
h= 10
h= 01
1 2 3 4 5 6 l 7 8 9 10 11
a
l0
Figure 5.3. Relation entre la charge et la longueur de la fissure
pour 80 = 0.1.
| 


