4.3 Formule donnant le facteur d'intensité de
contrainte :
Le facteur d'intensité de contrainte en pointe de fissure
est donné par :
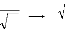
) (4.31)
(#177;la ) = du lim la2 --
X2 yi(X ) = -- du la lim 1--
s2 f (s
k3 1, , x #177;la 1 1
2 s #177;1
z ta
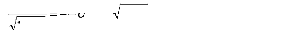
s
f
2
2
n
1 x
1
-
Tn (x)dx 1
= Un 1(s) 1-- s
(4.35)
Où v(x1) est donnée avec (3.24)
. On obtient :
N
2
k3 (#177;la) = lat_--
rc arccos(q) -- '2 An)
(4.32)
ir
4.4 Formule donnant l'ouverture de la fissure :
L'ouverture de la fissure en x1 E [-1,1] est
définie par :
1
8(x1)=w(x1,0+)--w(x1,0)=
I' lv(t)dt (4.33)
De (4.3), (4.7), (4.14) et (4.17) on obtient :


JI
~r 1_172 --17 1--r2
b-r2 + 1-172r _2arccos 1

8(r)= 2a et: 1 r2
+tc[rln
it-u r 1-172 +17
1--r2 r2 --
-- +17ln


172 0 -- r2

N A U i(r)
'
--la 1--r2E (4.34)
n=1 n
Pour obtenir (4.29), on a utilisé les relations suivantes
:
On observe à partir de l'équation (4.29),
que 8(r) n'est pas définie en #177;ç , a cause
des singularités logarithmiques. L'ouverture de la fissure en ces points
et obtenue en passant a la limite de 8(r) lorsque r ?
#177;ç.
On obtient les résultats suivants :

la
1
~l
a
~ ~
~ l a ~
J ô8 Ir JJ W:Jj
lala
2
ôalaarcco2ôa
2
la
la
la
11(
2la
la
1
-
)
8(#177;
Ir
la
Iru
~la
2 4u2n- la )
2
N
n=1
2n -1
4.36
4.5 Etude de convergence :
Nous avons étudié la convergence utilisant les
programmes relatifs aux différentes phases de développement de la
fissure pour déterminer les valeurs de N et n pour lesquelles il y'a
convergence. Pour déterminer l'une il faut fixer l'autre.
On commence par N , on prend n =100. On considère la
valeur du facteur d'intensité de contrainte K3 , la figure
4.5 montre qu'a partir de N = 30 K3 converge.
-20
|
-25 -30 -35 -40
k3
-45 -50 -55 -60 -65
|
|
-70
0 10 20 30 40 50 60 70
N
On considère maintenant n, avec N = 30 on obtient les
valeurs de facteur d'intensité de contrainte k3 en fonction
de n (figure 4.6). Il est clair que pour n =100 il y'a convergence.
|
0 -10 -20 -30 -40
k3 -50 -60 -70 -80 -90 -100
|
|
|
|
0 20 40 60 80 100 120 140 160 180 200
|
n
|
Figure 4.6.Valeur de facture d'intensité de contrainte
k3 en fonction de n.
Par conséquent, dans tout ce qui suit les calculs sont
effectuées avec N=30 et n=100.
=
=
Il
213
, 223
ax2
1
a W a W
Il
ax
(4.38)
4.6 Etude du cas de fissure dans un milieu infinie :
Dans ce paragraphe on considère le cas d'un plan infini S2
= (-00,+00)x (-00,+00) , contenant une fissure D
=[-10,10]x{0} centrale de longueur 210 . Le
matériau est élastique isotrope caractérisé par un
module de cisaillement Il . Les faces supérieure et
inférieure sont soumises à une contrainte de cisaillement
anti-plan positive et uniforme 200, augmenté a
partir de 0. Les lèvres ne sont pas chargées (figure 4.7).
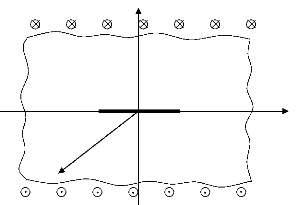
200
x2
x1
- 10 10
200
x3
Figure (4.7). Fissure dans un milieu infini.
Apres la superposition on considère que le problème
fissuré avec fissure chargé. Le modèle de fissure est le
modèle de DUGDALE.
4.6.1 Equation intégrale :
La seule composante non nulle du vecteur déplacement, et
la composante dans la direction x3, cette composante est
indépendante de x3 .i.e :
U1 = U2 = 0, U3 = W(x1, x2) (4.37)
Donc, le champ de contrainte correspondant est donnée par
:
|
211
|
= 222 = 233 =
|
212
|
=
|
0
|
On note que ce problème consiste à
déterminer la réponse de problème de la bande
fissuré lorsque les contraintes de cisaillement -- rcon sont
appliquées sur les lèvres de la fissure. Les faces
supérieures et inférieures de la bande sont libres.
Ainsi le champ de déplacement W et les deux composantes
non nul du champ de contrainte r13 et
r23 doivent satisfaire le système d'équation suivant
:
~AW = 0 ~~r.n = --r .n
co
~r23 = 0 ~ ~r23 = 0
dans II/ D
sur D (4.39)
sur x2 = 1-co
sur x2 = -co
En suivant les mêmes étapes que dans le chapitre 2
on arrive à l'équation intégrale suivante :
1
f
Il
-
1
ço(t) .dt = r(x)
x -- t
(4.40)
Le terme r(x) est la charge si on considère le
modèle de DUGDALE donné par :
<
si
1c
x1
r(x1)
<
si
1a
1c
< x1
~--r co , = ~
~--rco-Frc,
(4.41)
4.6.2 Phase cohésive :
La zone cohésive apparaît et se développe
dés que rco > 0 . Le critère gouvernant la
propagation de la pointe de la fissure 1a est k3 = 0 .
C'est une équation implicite relient
rco et 1a . La relation qui donné le
facteur d'intensité de contrainte pour le présent problème
et donné par :
k3

2
)) (4.42)
(#177;1a ) = 1a (rco-- r
aar cos(1 0
Ir 1a
La phase cohésive est caractérisé par un
facteur d'intensité de contrainte nul au pointe cohésives
1a .
(
r
co -- 2
r
a
ar
cos(1 0 )) =
1 a
Ir 1a
0 (4.43)
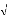
k3 (#177;1 a) = 0
Donc on arrive à la relation suivante qui donne
l'évolution de la longueur 1a en fonction du chargement a
8c fixe dans la phase propagation :
rco = 2 r aar cos(10 )
(4.44)
Ir 1 a
4.6.3 Contrainte de rupture :
La phase cohésive cesse lorsque l'ouverture aux points
x1 = #177;la dépasse la valeur critique
8a .
Elle est caractérisée par les deux relations
suivantes :
k3 (#177;la) = 0 ,
8(#177;la) = 8a (4.45)
On note que l'ouverture est donnée par la relation
suivante :
Ir
8(#177;la) = - Tal0Ln(cos r
T ) (4.46)
2
4Iru
T

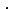
a
Donc :
8a =-
T
al0Ln
Iru
4 Ir TT
(cos
2T
)
)
Ir TT
cos(
2 Ta
= exp(- 8° c l) (4.47)

0
4Ta
La charge de rupture est donnée par la relation suivante
en fonction de 8a :
Ir
8irp
TT =2Ta aT
cos(exp(-
4a )) (4.48)
0
Ta


4.6.4 Phase de propagation :
Nous allons prouver que TT est
réellement la charge maximum que la structure peut
supporter tout en vérifiant l'équilibre et les
critères relatifs à la théorie de rupture. La
méthode la suivante :
On considère les relations suivantes :
[w]=8a (4.49)
On augmente la charge jusqu'à ce que T
=TT
Sachant qu'au deux points la et la :
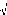
)) = 0
k3 (la) = 0 (4.50)
(
T
8- 2
T
c
aT
cos(l
a
la
Ir la
)
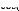
2
Ta
la= IrT8
cos(
la
(4.51)
À la pointe la on a :
))
[w(la) ]= 8a (4.52)
2
8 = (-2r l Ln
a c c
4
Iru la
(la
))
8a=-
TalaLn(cos(ler8
Iru
Ta
2
11-2
8c = 4rcl a
cos(le r" )Ln(cos( " ))
(4.53)

Irc Irc
gIi
la
iz-8
Ii
Donc on arrive à la relation suivante qui donne
l'évolution de la longueur la en fonction du chargement a
8c fixe dans la phase propagation :
_
(4.54)
c
gr
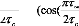
gr"
"
4rc cos(Ln
Irc Irc
)
| 


