4.2.3 Évaluation numérique des
différentes intégrales :
Les intégrales H (r i) et g(ri) sont
évaluées en utilisant la formule d'intégration de
GAUSS-CHEBYSHEV qui s'écrit :
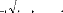
1 f (t)dt f (tk)
f2 ~
» ,
1
t --
1
1
-
p
7 (t k) = 0 (4.24)
La valeur de g(ri) du coté droite de
l'équation (4.23) est déterminée à partir de
l'équation (4.11) laquelle grâce à l'équation (4.14)
peut se mettre sous la forme suivante :
|
1 1
1g(r) = -- [f l aL(r,s)h1(s)ds
+ f laL(r,s)h2(s)dsj
|
(4.25)
|
La première partie est évaluée par la
précédente formule de GAUSS-CHEBYSHEV. A cause des
singularités logarithmiques que présente le terme h2
(s) aux points #177;77 , la seconde partie est devisée sous la
forme suivante :
1 --77 77
1
faL(r, s)h2 (s)ds = f laL(r,
s)h2 (s)ds + f laL(r,s)h2(s)ds + f
laL(r,s)h2(s)ds (4.25 bis)
1
--
1 --77 77
Chacun des intégrales du membre droit de l'équation
précédente est évaluée à l'aide de
GAUSS-CHEBYSHEV.
4.2.4 Evaluation numérique de L(r, s) :
Considérons maintenant le terme L(r,s)de l'équation
(4.10), après introduction des entités normalisées :
+c
.e
L(r, s) =e + e Âji . sin la
.2.(s --
2

0
(4.26)
--
Âh
AL(r,s) =
l .2.(s -- r d2.
a
(26 bis)
sin
)
·
f 2.e 2 e--
J --2 h 2 h
·
. sin la .2. (s--r).d.l + f
. '
·h
--2.h 2
e + e . e + e
0
A
Ou A est un point de coupure, La deuxième intégrale
du membre droit de l'équation précédente devient
négligeable pour une valeur de A suffisamment grande.
- Evaluation de A :
On considère la plus grande valeur de$ -- r = 2, pour
l'instant on prend la =10 .
L'évaluation numérique de l'intégrale
à l'aide du logiciel MAPLE avec la fonction (evalf) avait donné
:

)
=
0.05.
(4.27)
+00
(1e _2.h.e + e a.h .sin
20.2.la.d2
2
2.
h
evalf
-
0
Si on limite l'intégration sur l'intervalle [0.6] on
obtient une bonne convergence :
6r 2.e_a.h
evalf (f 21a (r -- t).d2)=
-a.h a h
e + e.
0
0.04999946939. (4.28)
En conclusion on peut limiter l'intégration sur
l'intervalle [0.6] et l'intégrale L(r, $) prend la forme suivante :
L(r,$) =e-2.h sin 21 afr --
t).d2.
+ e a.h
6

0
(4.29)
L'intégrale ainsi définie est évaluée
à l'aide de la formule de GAUSS-CHEBYSHEV avec un changement de variable
pour passer de l'intervalle [0.6] à l'intervalle[-1,1].
A
-1 2 2 A
(4.30)
A
(2+1).h
L(r,$) = A e A . sin (2+
1).la(r --t).d2.
2 - (2+1).h (2+1).h 2
1 e 2 + e 2
Avec : A = 6.
A l'aide de la méthode d'intégration de
GAUSS-CHEBYSHEV nous avons évalué numériquement
l'intégrale L(r,$), la est pris égale a10, le nombre
de points pour lequel il y'a
convergence de l'intégrale et n = 250. La valeur de
la =10 est choisi comme une valeur
limite au delà de laquelle la convergence ne peut
être attente qu'on augmentent n , ceci augmente sensiblement le temps
d'exécution des programmes relatives aux phases cohésive et
propagation (dans lesquels le programme est incorporé) et demande des
machines de calcul puissantes.
Pour une plage de valeurs de 2 on trace les deux
graphes dans les figures (4.3, 4.4) suivants :

0.08
0.07
0.06
L
0.05
0.04
0.03
0.02
0.01
62
0.08
0.07
0.06
L
0.05
0.04
0.03
0.02
0.01
0 10 20 30 40 50 60 70 80 90 100 110
A
Figure 4.3 : valeur de L(r, s) en fonction de A .

0 5 10 15 20 25 30 35
A
Figure 4.4. Agrandissement.
Il est clair que l'intégrale L(r, s) tend vers la
valeur de 0.5 même à partir de la valeur A = 6 . Ce
résultat a été prouvé avant par l'évaluation
de la même intégrale par le logiciel MAPLE, à l'aide de la
fonction (evalf) on retrouve la même valeur.
| 


