Chapitre 5
Approche théorique de résolution
5.1 Présentation de la méthode de Recherche
Tabou
La méthode Tabou est une technique itérative
généralepour 'optimii sation combinatoire, introduite par FRED
CLOVER en 1977 et développée plus tard. La recherche Tabou est
considérée comme étant une puissante proo cédure
d'optimisation capable dorganiser et de diriger es opérations d'une
méthode subordonnée.
La Recherche Tabou a remporté un immense succès
dans de nombreux proo blèmes d'optimisation combinatoire à savoir
les problèmesd'affectations quaa dratiques ainsi que l'ordonnancement et
autres.
5.1.1 Principe de la méthode de Recherche Tabou
La procédure de la Recherche Tabou est destinée
àtrouverun minimum global d'une fonction F définie sur un
ensemble desolutions réalisablesX. pour chaque solution S de X on
définit un voisinage N(S) constitué de toutes les solutions
réalisables qui peuvent être obtenues par'application d'une simple
modification m sur S.
La procédure commence par une solution
réalisable initialeet tente d'att teindre un optimum global du
problème par un déplacement àchaque étape,
dés qu'une solution réalisable est obtenue, on
génère un soussensembleV* de N(S) et on se
déplace versla meilleure solution S* dans V *. Si l'ensemble
N(S) n'est pas très large, il est possible de prendreV* =
N(S).
L'utilité du critère du meilleur
déplacement dans la Recherche Tabou est basée sur la supposition
que des placements avec beaucoupd'évaluations ont de plus grandes
probabilités datteindre une solution optimale ou proche de l'optimal) en
peu d'étapes.
Afin d'échapper aux minimums locaux, le
déplacement vers S* est effectué même si
S* est plus mauvaise que S (F(S*) = F(S))
1. Liste Tabou
La stratégie de la Recherche Tabou peut clairement nduiree
ccycle de l'algorithme. Afin de prévenir cela, on introduit une liste
notée T Cette liste contient les modifications effectuées dans un
passéde T étapes de l'algorithme.
Lors de la constructionon introduit la
génération des solutions qui sont obtenues de S par application
inverse mémoriséedans a iste Tabou.
Le principe réduit le risque de cyclage dés lors
qui nous ne garantisse pas un retour pour un nombre donné dirritations
à une solution déjà visitée au par avant.
2. Critère d'aspiration
Malheureusement, la liste Tabou pourrait jouer le
rôlequi consiste ànterdire de se déplacer vers des
nouvelles régions susceptiblesde contenir de meilleures solutions. Dans
le but davoir une plus grande iberté dans la génération
d'un sous-ensemble V il devrait être possible de perdre le statut Tabou
d'une modification quandil sembleraisonnable de e faire. C'est pourquoi
onintroduit pour chaque valeur possibleZde a fonction objectif une valeur
daspirationA(Z). une solution Sdans N(SS qui veut devenir Tabou à cause
de lalisteTabou peut quand même être prise en compte si F(S) <
A(F(S)), la fonction A est appelée fonction d'aspiration.
3. Critère d'arrêt
La règle pouvant être définie pour
interromprele déroulement du processus de la Recherche Tabou est
darrêterdés quemax térations sont effectuées sans
diminuer la valeur de la fonction objectifqui correspond à la solution
courante atteint une valeur Fmn de F qui est connue dans certains
problèmes.
Remarque
La notationS = S m veut dire : S est obtenue à partir de S
par application de la modification mi.
5.1.2 Algorithme général de la méthode
Recherche Ta- hou
1. Générer une solution réalisable S dans
X
S() :=S; S() la meilleure solution rencontrée
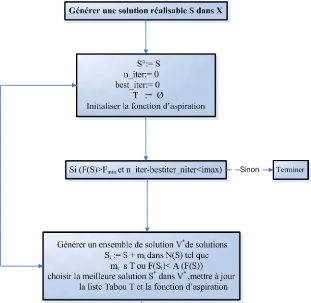
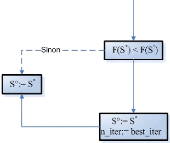
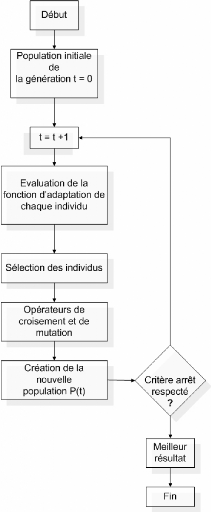
FIG. 5.1 Organigramme de la méthode de Recherche Tabou
niter := 0; Compteur d'itérations
bestiter := 0; L'itération à laquelle une meilleure
solution aététrouvée. T:=Ø;
Initialiser la fonction daspiration
2. Tant que (F(S) ~ Fmnetniter - bestiter < imax)
faire :
Générer un ensemble V * de solutions Si = S midans
N(S) tel que : mi ? T ou F(Si) <A(F(S));
choisir la meilleure solution S* dans V *
mettre à jour la liste Tabou T et la fonction daspiration
SiF(S*) < F(S()) alors
S() := S* ;
Bestiter := niter ;
S:=S*; Fin;
5.2 Les algorithmes génétiques
L'observation des phénomènes biologiques est
unetrès riche source d'inss piration pour les ingénieursLe
concept dalgorithme génétique notamment,
généralisé ces dix dernières années sous le
termed'algorithme évolutionnaire en est un excellent exemple. Les
principes de base de ces algorithmes on dit aussi "AE" pour "Algorithme
évolutionnaire") sont une transpositionnforr matique simplifiée
de la très célèbre théorie de Darwin.
En d'autres termes, on imite au sein dun programme
lacapacité d'une population d'organismes vivants àsadapter
à son environnement à'aide de mécanismes de
sélection et d'héritage génétique.
5.2.1 Historique
La transposition des principes dévolution darwinistes
entechnique d'opp timisation globale est née indépendamment des
deux côtés de 'océanAtlann tique il y a une quarantaine
d'années
L'idée maîtresse en est l'imitation du
phénomènedapprentissage collectif ou d'adaptation d'une
population naturelle.
Deux courants ont évolué parallèlement
usquà ily a une quinzaine d'ann nées, chacun ayant son champ
d'application propre.La récente fusion de ces différents courants
sous le terme dalgorithme évolutionnaire est corrélée
à leur attrait actuel pourles chercheurs et les industriels,
grrcenotamment à la vulgarisation des calculateurs parallèles et
à 'accroissement despuissances de calculs.
Le courant américain, initialisé par Hollanddans
les années soixante, est à l'origine de ce que l'on appelleles
Algorithmes Génétiques AG). Bien qu'ils aient été
prévus initialement dans le cadre doptimisation ou d'adaptation dans le
domaine discret, les AG ont été facilementétendus à
'optimisation sur des domaines continus.
En Allemagne sont apparuesà peu près en
même temps, des méthodes appelées Stratégies
d'Evolution (SE) Ces méthodes étaient au contraire
préé vues pour explorer des domaines continus, et ont
été étendues à desapplicaa tions en optimisation
discrète
Ce livre est issu d'un certain nombre didées et de
concepts sur esquelsl a travaillé à partir des années
60Quelques-uns deses élèves à 'universitédu
Michigan ont pris la suite.
Jusque dans les années 80, l'intérêt pour ces
méthodes étaitplutôt anec dotique car il existait assez peu
dapplications réelles.
Durant cette même décennie sont apparues de
nombreuses applicationsdans des domaines très divers. Les travaux de
Goldberg,et notamment ses app plications au contrôle de pipelines de gaz
en sont un exemple maintenant classique.
5.2.2 Mécanisme
Le principe de base des algorithmes génétiques
est la manipulation de po0 pulations qui évoluent sousl'action
dopérateurs stochastiques.Lévolution est usuellement
organisée en générations et copiede
façontrès simpli~éea génétique naturelle.
Les moteurs de cette évolution sont dune part
asélection, iée àa perr formance d'un individu, vis
à vis du problème que lon cherche à résoudre, et
d'autre part les opérateurs génétiques, usuellement
nommés croisement et mutation, qui génèrent lesindividus
dune nouvelle génération action d'exx ploration).
L'idée fondamentale des algorithmes
génétiques est a suivante e paa trimoine génétique
d'une population donnée contient potentiellement a soo lution, ou
plutôt une meilleure solution au problème donnéCette
solution n'est pas exprimée car la combinaison génétique
sur laquelle elle repose est dispersée chez plusieurs individus ; ce
n'est que par lassociationde ces combinaisons génétiques au cours
dela reproduction quea solution pourras'exx primer.
De cette façon, de génération en
génération, les meilleursgènes se proo pagent dans la
population, en se combinant et en échangeant esmeilleurs traits.
5.2.3 La boucle évolutionnaire
1. la reproduction: sélection des parents parmi une
populationde ,t individus pour engendrer À enfants;
2. croisement et mutation à partir des À individus
engendrant les À enfants;
3. évaluation des performances des enfants
4. sélection pour la survie de ,t individus parmi les
À enfants et ,t parents selon les paramètres choisis pour
lalgorithme, afinde formera population à la génération
suivante.
Pour l'utiliser, on doit disposer des cinq éléments
suivants
1. Un principe de codage des éléments de la
population
Cette étape associe à chacun des pointsde
lespaced'état une structure de données en éléments
sur lesquels peuvent s'appliquer es trois opérateurs
présentés ci-dessous.
Le choix du codage des données conditionne le
succès des algorithmes génétiques. Les codages binaires
ont ététrès emplooyés à 'origine.
Les codages réels sont désormais largement
utilisés, notamment dans les domaines applicatifspour loptimisation de
problèmes àvariables continues.
Ce codage intervient après une phase indispensablede
modélisation mathématique du problème.
2. Un mécanisme de génération de la
population initiale
Ce mécanisme doit être capable de produire une
population d'individus non homogène qui servira de base pour les
générations futures. Le choix de la population initiale est
important car lpeut rendre plus ou moins rapide la convergence vers loptimum
global.
Dans le cas où l'on ne connaît rien du
problème àrésoudre, lest essentiel que la
populationinitiale soit répartie sur tout edomaine de recherche.
3. Une fonction de performance :
Celle-ci prend ses valeurs dans R+ ; elle est
appelée fitness ou fonction d'évaluation de l'individu. Elle est
utilisée pour sélectionner et reproduire les meilleurs individus
de la population.
4. Des opérateurs de croisement et de mutation
Ces opérateurs permettent de diversifier la population
aucours des générations et d'explorer lespace détat.
Lopérateur de croisement recompose les gènes d'individus
existants dans la population, 'opérateur de mutation a pour but de
garantir lexplorationde 'espace d'état.
5. Des paramètres de dimensionnement
Taille de la population, critère darrêt,
probabilités de croisement (Pc) et de mutation (Pin).
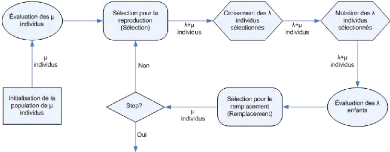
FIG. 5.2 Organigramme del'algorithme
évolutionnairegénétique
5.2.4 Description détaillée des
éléments de llalgorithme
Codage des données
La première étape est de définir et de
coder convenablement eproblème. A chaque variable d'optimisation xi,
nous faisons correspondre un gène. Nous appelons chromosome un ensemble
de gènes.
Chaque solution est représentée par un individu
doté d'un génotype constitué d'un ou plusieurs
chromosomes. Nous appelons populationun ensemble de N individus que nous allons
faire évoluer
Un chromosome est un tableau de gènes (Fig 4.3) Un
individuest un tableau de chromosomes. La population est un
tableaud'individus.
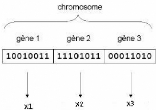
FIG. 5.3 Illustration schématique du codage des variables
xi.
On aboutit à une structure présentant cinq
niveauxd'organisation(ig 4.2):
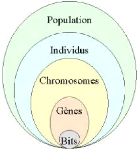
FIG. 5.4 Les cinq niveaux d'organisation de l'AG
Historiquement, le codage utilisé par les algorithmes
génétiques était ree présenté sous forme de
chaînes de bits contenant toute 'informationnécess saire à
la description d'un point dans lespace détat.Ce type de codage a pour
intérêt de permettre de créer des opérateursde
croisement et demutaa tion simples.
Pour des problèmes d'optimisation dansdes espaces de
grande dimension, le codage binaire peut rapidement devenir
mauvais.Généralement, chaque variable est
représentée par une partiede la chaîne de bits eta
structure du problème n'est pas bien reflétée lordre des
variables ayant une mportance dans la structure du chromosome, alors quilnen a
pas forcément dansa structure du problème.
Les algorithmes génétiques utilisant des
vecteurs réels évitent ce proo blème en conservant les
variables du problème dans le codage de 'élément de
population, sans passer par le codage binaire intermédiaire.
Génération de la population initiale
Elle est usuellement aléatoire (diverses
stratégies sont d'ailleurs envisaa geables pour échantillonner
correctement un espace de recherche complexe ou de grande dimension).
Le choix de la population initiale dindividus conditionne
fortement a rapidité de l'algorithme.
Si la position de l'optimum dans l'espace détat est
totalement nconnue, il est naturel d'engendrer aléatoirement des
individus en faisant des tirages uniformes dans chacun des domaines
associés aux composantesde 'espace d'état, en veillant à
ce que les individus produits respectent es contraintess Si par contre, des
informations à priori sur le problème sont disponibles, l
paraît bien évidemment naturel dengendrer les individus dans un
sous-domaine particulier afin d'accélérerla convergence.
Dans l'hypothèse où la gestion des contraintes
ne peut se faire directe ment, les contraintes sont généralement
incluses dans e critère à optimiser sous forme de
pénalités.
Opérateurs
A- Opérateurs de sélection :
A chaque génération, des individus se reproduisent,
survivent oudisparaissent de la population sous lactiondedeux
opérateursde sélection
~ la sélection pour la reproductionou plus simplement
sélection, qui dé-
termine combien de fois un individu sera
reproduit en une génération
~ la sélection pour le remplacementou toutsimplement,
le remplacement, qui détermine quels individus devront
disparaîtrede la population à chaque génération
La capacité d'un individu à être
sélectionné, que ce soitpour a reproduction ou pour le
remplacementdépend de sa performance un ndividu sera
sélectionné d'autant plus souvent quilest meilleurr l faut donc,
qu'une valeur de performance soit attachée àchaque ndividu, et
qu'elle soit évaluée pour les nouveaux individus
créés lors de chaque générationn
(a) Sélection pour la reproduction
On trouve dans la littérature un nombre important de
principes de sélection plus ou moins adaptés aux problèmes
quils traitent, parmi ces principes nous citerons
~ N/2-élitisme :
Les individus sont triés selon leur
fonctiondadaptation. eule la moitié supérieure de la
populationcorrespondant auxmeilleurs composants, est
sélectionnée. Il a été constaté quecette
méthode induisait une convergence prématurée de
lalgorithme a pression de sélection est trop forte
Il est en effet nécessaire de maintenir une
diversité génétique su~- sante dans la population,
celle-ci constituant un réservoirde gènes pouvant être
utiles par la suite.
- La méthode de la roulette :
Cette méthode, appelée aussi Roulette wheel
selection, RWS, consiste à associer à chaque individu un segment
dont a longueur est proportionnelle à sa fonction de performance.On
reproduitci le principe de tirage aléatoire utilisé dans les
roulettesde casinos avec une structure linéaireCes segments sont ensuite
concaténés sur un axe que l'on normalise entre 0 et 1. On tire
alors un nombre aléatoire de distribution uniforme entre 0 et 1, puis on
"observe" quel est le segment sélectionné
Avec ce système, les grands segments, cest-àdire
les bons ndividus, seront plus souvent choisis que les petits.
Lorsque la dimension de la population est réduite,
ilest di~- cile d'obtenir en pratiquel'espérance mathématique de
sélection en raison du peu de tirages effectués.
- La méthode de la roulette modifiée :
Cette méthode, appelée aussi Stochastic remainder
without replacement selection, SRWRS, découle de celle de la
roulette.
La SRWRS évite le problème rencontré dans
la méthode précédente et donne de bons
résultats
Le principe de cette méthode consiste tout dabord,
àsélecc tionner n individus (n À) tel que:
~ l'individu xi est sélectionné si sa valeur de
performance est supérieure à la moyenne (moy) de toutes les
performances
~ chaque individu xi est représenté m(xi) fois
où m(xi) est la partie entière du rapport de la valeur de la
performancede xi et la moyenne de toutes les performances (moy) :
[h'(xi) ]
m(xi) := moy
Ensuite, la sélection des (À - n) individus
restants se fait par la méthode RWS.
(b) Sélection pour le remplacement
Le remplacement gère la constitution de la
génération (g + 1).
Pour cette sélection aussi, il existe plusieurs
stratégiespour constituer la génération suivante.Par
exemple les stratégies d'évoo lution (u, À) et (u +
À) signifient que À descendants sont générés
à partir d'une population de u individus.
La stratégie "," consiste à gérer
l'élitisme par le biais de la différence (u - À) (on garde
les (u - À) meilleurs individus de la population courante et on
complète par les À descendants), tandis que la stratégie
"+" est une version plus adaptative dans sa gestionde l'élitisme :
à partir d'un ensemble intermédiairedetaille u+À
constitué des u individus de la population courante et des À
descendants, on sélectionne les u meilleurs individus de la
génération suivante.
la génération g + 1 les enfants engendrés
à la génération g. Ainsi on a u= À.
B- Opérateurs de variations
(a) Opérateur de croisement
Le croisement a pour but denrichir la diversitéde la
population en manipulant la structure des chromosomes.
Classiquement, les croisements sont envisagés avecdeux
parents et génèrent deux enfants.
Initialement, le croisement associé au codage
parchaînesde bits est le croisement à découpage de
chromosomes (slicingcrossover). Pour effectuer ce type de croisement sur des
chromosomesconstitués de M gènes, on tire aléatoirement
une position dans chacun des parents. On échange ensuite les
deuxsous-chaînes terminales de chacun des deux chromosomes, ce qui
produit deux enfants.
On peut étendre ce principe en découpant le
chromosome non pas en 2 sous chaînes mais en 34, etc
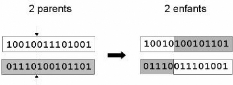
FIG. 5.5 - Représentation schématique du croisement
en un point
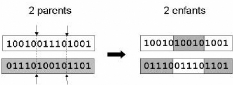
FIG. 5.6 Représentation schématique du croisement
endeux points
L'opérateur respecte généralement les
propriétés suivantes
~ le croisement de deux parentsidentiques donnerades descendants
identiques aux parents ;
~ par extension, deux parents proches lun de lautre dans l'ess
pace de recherche engendreront des descendants qui leur seront proches;
Le taux de croisement détermine la proportiondes
ndividus qui sont croisés parmi ceux qui remplaceront lancienne
génération.Plus le taux de croisement est
élevéplusil y aurade nouvelles structures qui apparaissent dans
la population. Mais ilne faut pasqu'ilsoit trop élevé car de
"bonnes" structures risqueraient d'êtrecassées trop vite par
rapport àl'amélioration que peut apporter a sélectionl ne
faut pas non plus qu'il soit trop faibles car la recherche risque de stagner
à cause du faible taux dexploration.
Le taux habituel est choisi entre 60% et 90%. (b)
Opérateur de mutation
L'opérateur de mutation apporte aux
algorithmesgénétiques la propriété
d'ergodicité de parcours despace.Cette propriéténn dique
que l'algorithme génétique sera susceptible datteindretous les
points de l'espace d'état, sans pour autantles parcourirtous dans le
processus de résolution
Pour les problèmes discretslopérateurde mutation
consiste géé néralement à tirer
aléatoirement un gène dans lechromosome et à le remplacer
par une valeur aléatoire.
La proportion des individus mutés dans la populationest
égale au taux de mutation qui est typiquement faible, de l'ordrede 0.001
et 0.05.
Un taux de mutation trop élevé rend la
recherchetrop aléatoire par contre avec un taux de mutation trop faible,
la recherche risque de se concentrer toujours sur les mêmes individus et
de mal explorer le domaine de recherche.

FIG. 5.7 Représentation schématique de la mutation
Critère d'arrêt
L'arrêt de l'évolution d'un algorithme
génétiqueest 'une desdifficultés majeures car il est
souvent difficile desavoirsi lon atrouvé 'optimum.
Actuellement les critèresles plus utilisés sont les
suivants
~ arrêt de l'algorithme après un certain nombre
de générations, fixé au départ; c'est ce que l'on
est tenté de faire lorsque l'ondoittrouverune solution dans un temps
limité
~ l'algorithme peut être arrêté lorsque la
populationnévolue plus ou plus suffisamment rapidement, c-à-d les
meilleurs individus nes'améliorent plus depuis un certain nombre de
générations.
5.2.5 Considérations sur la convergence des algorithmes
évolutionnaires :
On dira qu'un algorithme évolutionnaire a
convergé versunoptimum global si, après un nombre suffisant de
générations, au moins un ndividu a pu se trouver dans un
voisinage arbitrairement petitde cetoptimum.
La question de cette convergence se formule de la manière
suivante quelles sont les propriétés que doivent respecter es
opérateurs de variation et de sélection pour que la convergence
soit garantie ? Et dans ce cas, quelle vitesse de convergence peut-on
espérer?
Des réponses partielles ont été
apportées pour des représentations et opérateurs
particulierset des réponses précises existent mais seulementpour
quelques problèmes très simples.
5.2.6 Optimisation évolutionnaire avec contraintes
Les problémes d'optimisation doivent souvent respecter
uncertainnombre de contraintes. Celles-ci se traduisent par unensemblede
relationsquedoivent
satisfaire les variables qui sont généralement
exprimées comme un ensemble de q inégalités :
Gi(x) = 0 ?i = 1,..,q
où x est une solution du problème d'optimisation.
On appelle F l'ensemble des solutions réalisables
Dans le cas des algorithmes évolutionnaires, le vecteur
x est un individu. Les opérateurs de variation standard décrits
plus haut, poura représentation binaire ou réelle, engendrent des
individus de façon aveugle, ne tenant pas compte des contrainteset qui
peuvent correspondre à des solutionsrréalisables.
Les approches les plus classiques et les plus faciles à
mettre enoeuvre sont celles qui agissent directement sur la fonction de
performance, et ceci par l'application de méthodes de
pénalisation de afonctton de peeroomanne. Le principe est simple : la
performance dun individu irréalisable est réduite par la
soustraction d'une pénalité
fp(x) = f(x) - p(x)
où p(x) est définie dans le cas
général comme une fonction positive, croissante par rapport aux
mesures de violationdes contraintesçi(x), telles que :
f
çi(x) > 0 si la ieme contrainte n'est pas
respectée, çi(x) = 0 {sinon}. Typiquement,
P(x) = P( Xq áiçâ i
(x))
i=1
P : est une fonction croissante
ái : un coefficient positif dontla valeur est autant plus
grande qu'il est accordé d'importance au respect dela ieme
contrainte;
â: est fixée typiquement à 1 ou 2
Pour fixer les paramètresplutôt quutiliser une
pénalité statique, on a opté pour une
pénalité dynamique caril peut être avantageux de faire
varier les pénalités aussi bien dans ledomaineréalisable,
qu'irréalisableePuis, lorsque l'évolution est bien
avancée, les coefficients de pénalité doivent alors
prendre des valeurs élevées en faveur des individus
réalisabless
Comme méthode utilisant cette forme de
pénalité, on peut citer oines et Houk qui ont proposé en
1994 la fonction de pénalité suivante
Pi(x)=tk Xq áiçâ
i (x)
i=1
où :
t : représente le nombre de générations
accomplies k : prend la valeur constante de 1 ou 2
Calcul de la fonction de performance a- Fonction de performance
(fitness)
La construction d'une fonction de fitness appropriée
esttrèsmpor-
tante pour obtenir un bon fonctionnementdun algorithme
évolutionnairee On peut citer quelques caractéristiques de la
fonctiond'évaluation des
individus :
~ la fonction de performance dépend des critères
que 'on veut maximiser ou minimiser;
~ elle peut changer de façon dynamique pendant le
processus de recherche ~ elle peut être si compliquée qu'on ne
peut calculer que sa valeur approchée;
~ elle doit, si elle est correctement construite, attribuer des
valeurs très différentes aux individus afin de faciliter la
sélection
~ elle doit considérer les contraintes du
problème.S'ilpeut apparaatre des solutions invalides, la fonction de
fitness doit pouvoir attribuerune valeur proportionnelle au non respect des
contraintes
~ la valeur de la fonction de fitness peut être aussi
attribuée par'utilisaa teur.
On définit le "rang" d'un individu commele nombre
dindividus qui le dominent. Par exemple, si l'on considère un individu x
à la génération t qui est dominé par Pi(x), le rang
de l'individu considéré est donné par
Rangt(x) = 1 + Pi(x)
A tous les individus non dominés on affecte le rang 1Les
ndividus dominés se voient donc affectés un rang important.
Pour le calcule de l'efficacité, on passe par les
étapes suivantes
(a) classer les individus selon leur rang
(b) affecter une efficacité à chaque individu
en interpolant du meilleur (rang 1) jusqu'au plus mauvais (rang n), et cela en
utilisant une fonction linéaire dynamique ft(x) donnée comme suit
:
ft(x) = t x (,t + 1 - Rangt(x))
Pour ce type de méthode, le nombre de comparaisons
effectuéespar générations est égal à ,t x
(,t - 1) x k
où ,t correspond au nombre d'individus dans la population,
et k le nombre d'objectifs(Dans notre cas k=1)

| 


