Chapitre 6
Résolution du problème
Ce chapitre porte sur la description et la mise en oeuvrede
deuxméthodes heuristiques pour résoudre ce problème, entre
autre choisirdeux méthodes adéquates, les adapter au
problème, puis comparer les résultats etes performances des deux
méthodes.
6.1 Choix des méthodes
Notre choix s'est porté sur la méthodede la
recherche tabou etaméthode génétique. La résolution
peut être envisagéeen deux étapes, apremière
consiste à trouver une solution réalisablededépartpour
améthode recherche tabou, et un ensemble de solutions réalisables
pour la méthode génétique.La seconde étape consiste
à améliorer la solution obtenue dans a première
étape.
6.2 Justifications du choix
Rappelons que notre problème est un problème en
variables bivalentes. Si ce problème pourrait se formuler en un nombre
restreint de variables, on aurait pu peut-être utiliser une
méthode de séparation etévaluation par exemple, mais vu le
nombre important de variables, et compte tenu que ces variables soient
bivalentes, on était contraint àse diriger
versesmétaheuristiques.
1. Méthode 1
Vu la complexité du problème, la nature de la
fonction objectiffqui est non linéaire, et qu'il n'existe pas de
méthodes exactes pour a résolution de ce type de problème,
nous avons décidé derésoudrenotre problème avec une
métaheuristique Génétique
Ce choix est justifié par la facilité
dadaptation des algorithmes génétiques aux différents
problèmes, et par le temps decalcul de ces algorithmes qui est
acceptable, et aussi de vouloir comparer deux approches fondamentalement
différentes, la méthode génétique qui est une
méthode évolutive, etla méthode de recherche tabou qui
estune méthode séquentielle.
2. Méthode 2
L'application de la méthode Recherche Tabou " sur des
problèmes d'affectations de grande dimension, a
généralement abouti àdes résull tats très
satisfaisants, et envisageables dans a pratique si cetteméé thode
est bien exploitée, dansle sens ou lefficacité de cette
méthode générale, est flexible et dépendante
particulièrement de la façonde son adaptations au
problèmecest pour cela quon achoisi a méthode de la recherche
tabou comme méthode de résolution à
notreproblème.
6.3 Adaptation de la méthode génétique
L'adaptation de la méthode génétique
à un problème, consiste d'abord à établir un bon
codage dela solution, puis à ladaptationde tous esopérateurs de
cette méthode à ce problème, car en seins de ces
opérateurs que 'adapp tation sera la plus aigueet bien sûr
ladaptationde 'algorithme général, en choisissant les
probabilités de reproduction, et de mutation.
6.3.1 Codage de la solution et des données
Avant de procéder au codage de la solution, on
doitétablirun codage précis des données.
Codage des données
Pour le codage des donnéeson définieles variables
suivantes
1. NbNavire : représente le nombre de navires de
Sonatrach plus les navires susceptibles d'être affrétés
2. NbPort : représente le nombre de ports de
déchargement
3. NbMois : représente le nombre de mois de la
période détude
4. NbMaxRotation : représente le nombre maximum de
rotation que le navire le plus rapide pourra effectuer
Les données des navires et des ports de
déchargement, seront respectivee ment stockés dans les
enregistrements CelluleNavire et CellulePort, détaillé dans le
tableau suivant :
CelluleNavire=Enregistrement
Num : entier Positif ; {Numéro du navirej
Cap : entier Positif ; {Capacité du navirej
Vit: entier Postif ; {Vitesse du navirej
Deb : entier Positif ; { Débit de déchargement du
navire}
Fin;
CellulePort= Enregistrement
Num : entier Positif ; {Numéro du port}
CapMin: entier Positf{Capacité d'accueil minimumj
CapMax : entier Postf{Capacité d'accueilmaximumj
FraisP: entier Postf{Frais portuairesj
Deb : entier Positif ; {Débit de déchargement du
porttj
DMin :Tableau[1..nbPort,1nbMos]dentier Positif{Demandes
mensuelles minimumj DMax :Tableau[1..nbPort1nbMos]dentier Positif{Demandes
mensuelles maximumj Fin;
Codage de la solution
A fin d'économiser l'espace mémoireet de faciliter
la programmation de ces méthodes de résolutionson a opté
pour le codage suivantt
CelulleRotation =Enregistrement
J :entier positif ; {Jour de chargement de la rotationj
D :entier positif ; {Destination de chargement de la rotation
J
Q :entier positif ; {Quai de chargement de larotation}
Fin;
Sol =Tableaij[1..nbNavire,1..nbRotaton] de CeueRotation
Exemple
SoI[i,r].J : {Le jour de chargement de larotation r
e~ectuée par enavirei; SoI[i,r].D : {Le numéro de la destination
de la rotation r efectuée pare naairei; SoI[i,r].Q : {Le numéro
du quai de chargementde la rotation r efectuée pare naaire i;
Explication du codage de la solution
La solution du problème sera représentée
par une matrice, Sol, de taille NbNavire × NbMaxRotation, entre autre la
matrice Sol comporte NbNavire lignes, qui comporte chacune d'elles
NbMaxRotationde cellule CelleleRotaa tion.
Une cellule CelluleRotation, représente les
informations relative à une seule rotation, elle comporte trois entiers
positifqui représente respective ment, le jour de chargement de la
rotation,ladestinationde a rotation, ete poste de chargement dela rotation.
Notons que le navire qui effectue la rotation nest pas
représenté par un entier, il est en fait donné par
lalignede la cellule CelluleRotation, car chaque ligne représente les
rotations effectuées par un naviretout au ong de'année.
En fin, L'ensemble de la population (des solutions dune
génération sera représenté par le tableau
suivant
TSol=Tableau[1..100] de Sol;
Illustration
Le codage d'une seule solution estillustré dans lexemple
suivant.
Pour cet exemple le nombre maximum de rotation sera
égalà3, etenombre de navires sera aussi égal à 3
|
Rotation 1
|
Rotation 2
|
Rotation 3
|
|
Jour
|
Destination
|
Quai
|
Jour
|
Destination
|
Quai
|
Jour
|
Destination
|
Quai
|
|
Navire 1
|
5
|
6
|
2
|
14
|
2
|
3
|
0
|
0
|
0
|
|
Navire 2
|
4
|
3
|
5
|
30
|
5
|
5
|
49
|
1
|
5
|
|
Navire 3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Dans l'exemple précédent Le navire 1 effectuera
~ Le chargement pour sa première rotationle our verse
port6, à partir du poste de chargement 2
~ Le chargement pour la deuxième rotation le jour 14
verse port2, à partir du poste de chargement 3et aveccette rotation
enavire 1 accomplira sont programme
Par contre le navire 3, n'effectuera aucunerotation, ce navirene
serapas affrété.
6.3.2 Procedure Recherche de solutions réallsables
la procédure suivante génère une
solutionréalisable pour notre problème
Procedure Sol-réal(E/S Sol Solution) Var
i : entier positif ; {indice navirej
j : entier positif ; {indice port}
m : entier positif ; { indice moisj
DM :Tableau[1..nbMois] d'enter positif FM :Tableau[1..nbMois]
d'enter positif
{Les tableaux precedents representent les datesdedébut, et
dea fn des mois dea durée détude Exemple : FM[mJ : date dela fn
du mois[m]}
QT :réel;
{QT est utilisé par l'algorithme pour calculera somme dea
quantitéransportée chaque mois vers leclient}
JourDisCour[i]Tableau[1Nb-Navire ] de entier positif
{Numéro du jour de disponibilité courant
dunavire[i]j
RotCour [i] : Tableau[1NbNavire ] de entier positif
{Numéro de la Rotation courantedu navire[iiJJ
Début
Pour m :=1 à Nb-Mois faire {pour chaque mois fairej
Tri-Aléa-Port(TabPort,NbPort)
{Cette procedure trie aléatoirement le tableau TabPortt
Le tri des ports selon l'ordre décroissant des
quantitésmensuelles aurais du nous donner une solution plus proche de
l'optimum que celle qui sera trouvéepareri aléatoire, mais on
doit introduire laléatoire
pour garantir de trouver un nombre important de solutions
réalisables diiferentes en unemps acceptable.}
Pour i :=1 à Nb-Navire faire {pour chaque navire faire}
Si jourDis[i] <DM[m] alors JourDis[i] :=DM[m] ; Finsi ;
Fait;
{Les demandes des mois précédents au mois[mJ
supposées satisfaites,a boucle précedente a~ecte auxjours de
disponibilité des navires qui pourront etreibre(disponiblee avantle
début du mois en cour a date de début
de ce dernier,pour garantir que les naviresne fassent pas de
rotations avant le début du mois en courr
Pour j :=1 à Nb-Port faire {pour chaque por[jJ faire J
Tri-Navire(TabNavire,nb-Navire)
{Cette procedure trie le tableau TabNavireconstitué de
CelluleNavire par ordre croissant du rapport (coût de Rotation du
navire[iijau port[jj/quantitéransportée parle navire[i[au
port[j[j/ De cette manière, on favorise lesnavires lesplus rentables, et
on fait un pas vers loptimumm
Suite de l'algorithme SolReal
|
I :=1; {Prendre le premier navire de la listeListeNavireAccc
QT :=0;
{ce compteur compte la quantité qui peut tre
transportéee paresotations affectéesjusquàla,
au port[jJ le mois en cour [mJJ
Tant que (QT<port[j].DMn[m]) et (i<Nb-Navire-Acc) faire
{si quantité QT ne satisfait pas
lademandeminimalemensuelle du port[j[j le
mois[mmJuiestreprésentéepar Port[j/.DMin[mJetles
naviresde la liste ListeNavireAcc ne sont pasous eeplorés, lors
pourccaque navire[i[de la liste ListeNavireAcc faireej
Si (JourDis[i] <FM[m]) et (QT+Navire[i] cap <= Port[j]DMax)
alors
{Si le navire[i] dela Liste ListeNavireAcc est disponible avantla
n du mois en cour et la quantité QT plus la quantité qui
peutêtre transportée parenavire[i] ne dépasse
paslauantité maaimale demandéepar le Port[j/ le mois en cour [mJ
alors}
Début Quai :=AffetQuai(TabNavire[i]JourDsNavire[i]) Si
quai<>0 alors
{si un quai compatible est disponiblee jour de
disponibilité de navire alors}
Début
SoI[i,RotCour[i]] J := JourDsNav[i] SoI[i,RotCour [i]] D :=j
SoI[i,RotCour [i]] Q :=Qua
{Affectation d'une rotation au navireTabNavire[i]}
Qt :=Qt+TabNavire[i] cap ; {mise à jour du compteur QTJ
RotCour [i] := RotCour []+1
{incrementer la Cellulerotation encourrj
JourDisNav[i] := JourDsNav[i]+DureeRotationIj]
{mise à jour de la date de disponibilitédu
navirei
Fin;
Sinon JourDisNav[i] := JourDsNav[i] +1
{si aucun quai compatible nest disponiblee jour
ourDisNav[i]alorsle navire est considéré comme indisponible
cejourla,donc le jour dedisponibilité du naviret incrementé par
unjourr
Finsi;
Fin;
Sinon i :=i+1;
{Si le jour de disponibilité du navire , dépassea
fn dumois en cour, on passe au navire suivant dans le tableau TabNavire J
Finsi; Fait; Fait; Fin.
|
Remarque 1
On a préféré donner l'algorithme
détaillé de la procédureSolReal, car cette
procédure est trés importante dans larésolution, et permet
à 'algorithme de résolution de faire un grand pas vers
loptimum.
Remarque 2
L'organigramme de cette procedure est donné parafigure
7..
6.3.3 Justification de l'algorithme SolReal
~ Le nombre de ports de déchargement est fini. A chaque
foisqu'on saa tisfait la demande d'un port, on passe à un autre portde
déchargement suivant l'ordre aléatoire des demandes. Les ports
sont triés aléatoire ment à chaque mois pour
générer un grand nombres de solutions réaa lisables
differentes. Le processus sarrêteradés qu'on parcourt touses
ports. Et à la fin de l'algorithme tous les ports seront satisfaits.
~ Le nombre de navires disponibles et compatibles avec un
portde déé chargement est fini et non nul, car les navires
disponibles dans a iste des navires candidats àl'affrétemetent,
qui comporte es navires de Sonatrach plus les navires susceptibles dêtre
affrétés sont argement suffisants pour satisfaire la
demandedetous les ports de déchargement.
~ L'algorithme exploreles navires compatibles selon
l'ordredutri établi par rapport à chaque portce tri se faitpar
'ordre croissantdu rapport (coût de la rotation du navire i vers le
portj) / (la quantité transporr tée vers ce port par cette
rotation decette maniire, on favorisees navires de meilleur rendement, donc on
effectue un pas vers 'optimum.
~ Une rotation n'est affectée à un navire
quedans e casoù enavire est disponible, plus exactement si il n'effectue
aucune rotation, et ondiss pose d'un quai de chargementle jour de chargement
dea rotation.La disponibilité du navire i est exprimée dans
lalgorithme par a variable " JourDisNav[i] ".
~ La disponibilité d'un quai de chargement un jour
donnéest vérifiée par la fonction " AffectQuai ", cette
fonctionrenvoieenumérodu quai si ce dernier est disponible, et renvoi
zéro si aucun quai nest disponible.
~ Si aucun quai n'est disponible le jour JourDisNav[iice
dernièr sera incrémenté d'un jour, et le navire sera
considérécomme indisponible jusqu'au prochain jour, car la
durée de chargement de tous esnavires est à peu près de
24h, contrairement aux durées dedéchargements qui sont
très différentes dun navire à un autre.
~ Les quantités transportées par les rotations
affectéesemois en cours, jusqu'à le jour en cours, sont
comptées par la variable QT sia somme de cette quantité avecla
quantité éventuellement transportée pare navire en cours
de traitement par lalgorithme se situe dansamarge de flexibilité de la
demande mensuelle du portet un quai compatible et disponible, et le navire
concerné est aussi disponible, une rotation sera affectée
à ce navire, qui aura comme jour de chargement e premier jour de
disponibilité du navire, de cette manière on minimise letemps de
repos des navires.
~ Lorsque on affecte une rotationà un navire il faut
précisera destination de la rotation, qui est tout simplement le
portencoursde traitement par l'algorithme, et il faut préciser aussi le
quai de chargement qui sera déterminé par la fonction "
AffectQuai "
~ A chaque fois qu'une rotation est affectée à
un navire, ejour de disponibilité de ce navire
seraincrémenté par le nombrede jour qu'ilmet pour faire cette
rotation.
6.3.4 Paramètres de l'algorithme
Génétique
Population initiale
Pour l'application de l'algorithmenous avons choisi de prendreune
population initiale de ,t = 100 individus, tous réalisables.
La génération d'une population non-homogène
se faitde manière aléatoire avec la procédure
"SolRéal"
6.3.5 Adaptation des opérateurs
L'opérateur de sélection
l'opérateur sélection sélectionne
À = 50 pour la reproduction, par la méthode la roulette
,détaillée dans le chapitre précèdent.Rappelons que
cette méthode favorise les individus les plus adaptés
proportionnellement àeurs fonction d'adaptation.
L'opérateur de croisement
L'opérateur de croisement permetde créerdes
nouvelles combinaisons des paramètres des composants. Nous avons choisi
dans notre cas d'utiliser le croisement à découpage de
chromosomes à un point.
Pour effectuer ce type de croisement sur des chromosomes, on
tire aléatoirement une position de croisement identique dans chacun des
parents.On échange ensuite les deux sous-chaînes terminales de
chacun des deux chromosomes, ce qui produit deux enfants
Pour ce qui est du taux de croisement nous avons choisi, Pc = 0,
6. Exemple
Soient deux individus X, Y tirés aléatoirement de
la population courante. Dans cet exemple, on croise àla 6ieme
position.
X = {2,2,1,2,3 ,
|{z} 5,1,1,3,4,5,4,0,0,0,0,0,0}
Y= {1,1,2,3,4 ,
|{z} 4,2,1,5,2,3,2,4,2,2,2,3,1}
Après croisement on obtient
X' = {2,2,1,2,3 ,
|{z} 4,2,1,5,2,3,2,4,2,2,2,3,1}
Y' = {1,1,2,3,4 ,
|{z} 5,1,1,3,4,5,4,0,0,0,0,0,0}
La procédure de croisement est décrite ci
dessous
|
Pour i := 1 à À faire
1- Tirer au hasard deux individus X et Y de la population
séléctonnée à la reproduction
2- Tirer aléatoirement et uniformément "r" un
réel entre 0 et 1 ;
3- Si (r < Pc) Alors
-Générer aléatoirement une position"P" ;
-Croiser les individus X et Y à la position "P" pour
obtenir X ' et Y'
Sinon
Garder les deux vecteurs X et Y;
Fin Si
Fin Pour
|
Algorithme 1: Procédure Croisement
L'opérateur de mutation
L'opérateur de mutation est un opérateur unaire,
générant un seul individu à partir d'un autre et qui
consiste àtirer aléatoirement un gène dans le chromosome
et àle remplacer par une valeur aléatoire.
Pour ce qui est du taux de mutation nous avons choisi, Pm = 0,
02. Exemple
Soit un individus X tiré aléatoirement de la
population courante. Dans cet exemple, on mute X à la 5ieme
position.
X= {2,2,1,2,3
|{z},5,1,1,3,4,5,4,,0,0,0,0,0,0}
Aprés mutation on obtient
X= {2,2,1,2,5
|{z},5,1,1,3,4,5,4,,0,0,0,0,0,0}
La procédure de mutation est décrite ci dessous
Pour i := 1 à À faire
1-Tirer un individus de la population
séléctionnée à la reproduc tion; 2-Tirer un
réel "a" uniformément dans [0,1] ;
2- Si (a < Pin) Alors
Muter l'individu:
2.1-Tirer au hasard une position i entre 1 et nbNavire 3- Si (Le
nombre de rotations affectées au navireest
superieure à 1) Alors
3.1-Tirer au hasard un jour j de lannée
3.2- Si (Le navire i effectue une rotation je jour j) Alors
Enlever la rotation r au navire i
Sinon
Affecter au navire i une nouvelle rotation, à partir du
jour j, si la contrainte Rotation est toujours verifiée
Fin Si
Sinon
Affecter au navire i une nouvelle rotation Fin Si
Fin Si
Fin Pour
Algorithme 2: Procédure Mutation
L'opérateur de sélection pour le remplacement
L'opérateur sélection pour le remplacement
sélectionne tout simplement les À = 50 plus mauvais individus
pour les remplacer avec les À = 50 meilleurs individus parmi les
i+À individus constitués par génération courante
plus les enfants reproduits parles opérateurs croisement etmutation.
Donc on utilise la stratégie (i + À), cette stratégie a
été détaillé dans le chapitre
précèdent.
Critére d'arrêt
le critère d'arrêt pour lequel on à
opté, est celui de fixer enombremaximum d'itération.
6.4 Adaptation de la méthode de la recherche tabou 6.4.1
Le codage de la solution
La solution qui sera créer et en suite manipuler par
'algorithme, sera représentée par le type Sol
déclaré précédemment.
6.4.2 Génération d'une solution
réalisable
Pour générer une sotution réalisable on
utilise la même Procedureuntisée pour générer des
solutions réalisables pour la méthode génétique,
avecune petite modification, au niveau du tri aléatoiredes
demandesmensuelles, qui sera remplacé par le tri décroissant des
demandes mensuellessOn peut se permettre de faire ce tricar avec la
méthode Tabou, onn'a pasbesoin de générer plusieurs
solutions differentes. Donc l'organigramme de a procedure qui gegère des
solutions réalisable pour la méthodedea recherche tabou, est
repésentée dans la figure 46
6.4.3 Génération des solutions voisines
La génération de solutions voisines est une
étape trésmportantedans l'application de l'algorithme de la
recherchetabou.Lalgorithme doit avoir accès à toutes les
solutions réalisables.
Pour cette raison qu'on definie lalgorithme suivant
|
1-Tirer aléatoirement deux navires N1 et N2de La iste
desnaviresaller
en 2
2-Tirer aléatoirement un mois parmi les mois de la
période d'étude aller
en 3
3- Si (N1 et N2 effectuent des rotations le mois m) Alors
3.1-Choisir aléatoirement de chaque navire une Rotation,
etes substituer
4- Si (la solution est toujours réalisable) Alors
aller en 8
Sinon
Aller en 1
Fin Si
Fin Si
5- Si (L'un des navires N1,N2 effectue des rotations le moism, et
'autre
non) Alors
5.1-Choisir aléatoirement une rotationdu premier navire
et'affec
ter au deuxieme
6- Si (la solution est toujours réalisablle) Alors
aller en 8 Sinon
Aller en 1
Fin Si
Sinon
8- Si (les deux navires N1,N2 n'effectuent aucune rotation emois
m)
Alors
Aller en 1 Sinon
Fin Si
Fin Si
8-Une solution voisine est générée,fin
|
Algorithme 3: Procédure Génération
desolutions voisines
6.4.4 Listes Tabous adaptées à notre
problème
Pour éviter le cyclage de l'algorithme, on définie
deux listesTabous, ListeTran et ListeSub.
1. ListeSub
Mémorise un nombre fixe de types substitutions de
rotations.es cellules de la liste sont représentées par des
Quadruplés dea forme suivante (Rotationi, Rotation2NavirelNavire2). et
on it(La rotation1 et la rotation2 effectuées respectivement par le
navire1 et enavire2 sont substituées), donc on interdira toute
candidatured'une solution obtenue par la modification inverse à celles
contenuedans la liste ListeSub.
2. ListeTran
Mémorise un nombre fixé de types transferts
derotations.es cellules de la liste sont représentées par des
triplés dea forme suivante (RotationÄ, Navirel, Navire2) . et
onlit(La rot ationÄsera transférée du navirel versle
navire2) donc on interdiratoute candidature d'une solution obtenue par la
modification inverse àcelles contenue dans la liste ListeTran
6.4.5 Tailles des Listes
En effectuant des tests, on a fixé les tailles des deux
listes à 7 Cette taille est trés envisageble dansl'adaptation de
la méthode recherche tabou.
6.4.6 Critère d'aspiration
Une solution tabou doit dans certains cas perdre son statut
tabou pour devenir candidate à la meilleure solution voisine, et
daméliorer ameilleure solution rencontrée, pour cela on definit
la fonction d'aspiration suivante A(F(s)) = F(s°).
6.4.7 Critére d'arrêt
Le critère d'arrêt pourlequel on à
opté, est celui de fixer enombremaximum d'itération.
6.4.8 Algorithme Recherche Tabou Adapté à notre
problème
Var
niter : entier positif ;
{Compte le nombre d'itération e~ectuées dans
'éxploration deouteses solution passéess
bestiter : entier positif; {Mémorise l'itération de
la meilleure solution retrouvéee
maxiter : entier positif ; {Nombre maximum d'itérationj
1-Trouver une solution initiale réalisable par la
procedure SolRéalTabou;
2-Initialiser les listes ListeSub et ListeTran;
3-niter := 0;
4-bestiter := 0;
5- Tant que (niter maxiter) faire
5.1-niter := niter + 1;
5.2- Tant que (il existe toujours des solutions voisines non
explorées et n nbV) faire
5.2.1-Générer s' une solution voisine
avec GénéVoisin 5.2.3- Si (f(s') < A(f(s)) ou (le
mouvement vers s' n'est pas dans listeSub ou listeTran)) Alors
ajouter s' à l'ensemble des solutions voisines
Fin Si
Fait
5.3-Retenir la meilleure solution dans lensemble des solutions
voisines;
'
5.4- s := s;
5.5-Mettre à jourles listes ListeSub et listeTrans
5.6-Mettre à jourla fonction daspiratonA
5.7- Si (f(s) <f(s°)) Alors
s° := s; bestiter := niter;
Fait
Fin Si
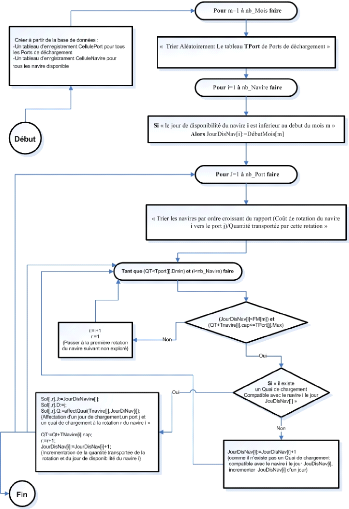
FIG. 6.1 Procédure population initiale
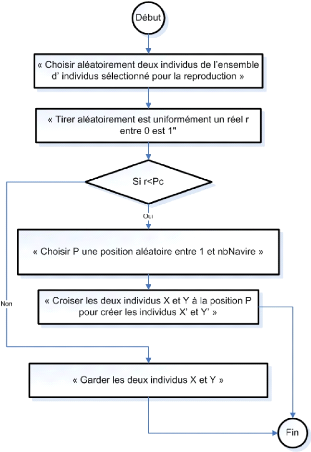
FIG. 6.2 - Organigramme de la procedure croisement
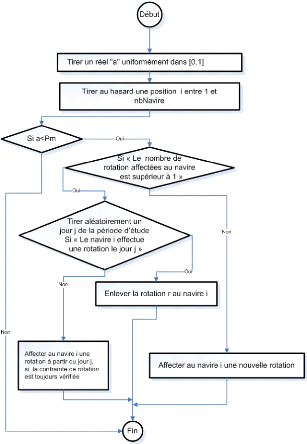
FIG. 6.3 - Organigramme de la procedure mutation
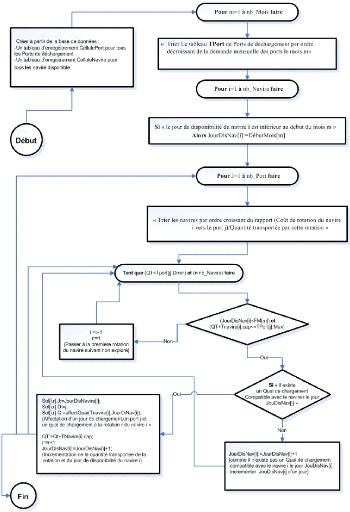
FIG. 6.4 Procedure SolRéalTabou
| 


