Identification géotechnique de matériaux concassés-types en corps de chaussées et évaluation de leur qualité

Chapitre 3. - Mélange et Compacité granulaires

1. - Les mélanges granulaires

Pratiquement, il n'est pas toujours facile de trouver un matériau granulaire naturel ou manufacturé satisfaisant et on est souvent amené à recomposer un granulat à partir de n autres.

1.1. - Les mélanges binaires

1ère méthode : Soit deux granulats (A et B), de masses respectives MT[A] etMT[B], que l'on

désire mélanger dans des proportions respectives _XA% ^et _XB% afin d'obtenir un granulat C (Gabrysiak, 2007). Le refus cumulé du mélange exprimé en % au tamis d'ouverture Di considéré est :

MT[ C ] = XA%MT[A] + XB%MT[B] R%[C]Di = X _A% R % [ A ] Di+ X B % R % [ B]Di

MT[C] = Masse totale du mélange A + B,

R%[A]Di = Refus cumulé exprimé en % de l'échantillon A au tamis d'ouverture Di ; R%[B]Di = Refus cumulé exprimé en % de l'échantillon B au tamis d'ouverture Di ; R%[C]Di = Refus cumulé exprimé en % de A + B au tamis d'ouverture Di.

2ème méthode (méthode graphique) : Sur les axes verticaux, on reporte les passants des granulats A et B pour chaque tamis (Gabrysiak, 2007). Puis on joint les points par une ligne appelée ligne de combinaison. Pour une proportion donnée de A dans le mélange (ligne verticale de mélange), on détermine le point de passage du mélange en % de passants (fig. 12).

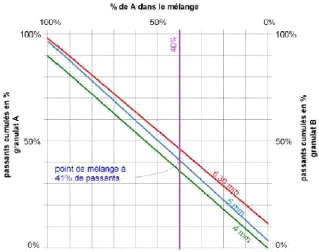
Fig. 12. - Les mélanges granulaires binaires : méthode graphique (Gabrysiak, 2007)
24

3ème méthode (méthode graphique appliquée aux fuseaux) : La méthode graphique est très pratique pour trouver les proportions d'un mélange situé dans un fuseau donné (Gabrysiak, 2007). Il suffit de reporter sur chacune des lignes de combinaison le maximum et le minimum (définit par le fuseau) pour chaque tamis et de joindre ces maxima et ces minima par des lignes brisées. Si ces deux lignes se croisent, il est impossible d'obtenir un mélange entrant parfaitement dans le fuseau. Si elles ne se croisent pas, le domaine situé entre les deux lignes verticales tracées à partir des points les « plus à l'intérieur » des deux lignes brisées définit la phase des combinaisons possibles qui satisfont aux exigences du fuseau (fig. 13).

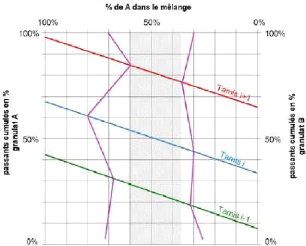
Fig. 13. - Les mélanges granulaires binaires : méthode appliquée aux fuseaux
granulométriques (Gabrysiak, 2007)

1.2. - Les mélanges ternaires

Dans un triangle quelconque ABC, tout point P situé à l'intérieur du triangle représente un mélange des trois composantes de base représentées graphiquement par les trois sommets du triangle dans les proportions XA, XB et XC (fig. 14).

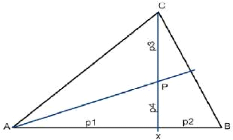
Fig. 14. - Détermination des proportions d'un mélange ternaire de granulats à partir d'un
triangle (Gabrysiak, 2007)

25

4

1

2

3

3

p

p

p

p

3 4

+ p

3 4

+ p

^{1 2}

p p

+p

^{1 2}

p p

+p

p

X C +

=

p p

3 4

X A = ×

X B = ×

X_A + X_B + X _C =1

De façon pratique, pour mélanger trois granulats on commence par se fixer les limites granulaires (gros, moyen, fin). On divise ensuite chacun des trois granulats utilisés en trois fractions qui détermineront les coordonnées de trois points représentatifs des trois granulats dans le diagramme triangulaire. On joint ces trois points qui forment un triangle (fig. 15).

On caractérise ensuite le fuseau imposé par un point représentatif P sur le même diagramme. Si le point P est à l'extérieur du triangle quelconque formé par les trois points représentatifs des granulats, il est impossible de combiner afin d'obtenir un mélange exactement conforme aux exigences.

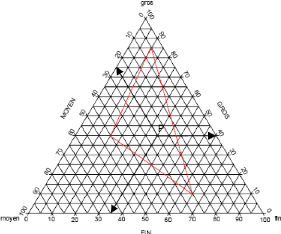
Fig. 15. - Les mélanges granulaires ternaires : méthode du diagramme triangulaire
(Gabrysiak, 2007)

2. - La compacité granulaire

2.1. - Mélange de deux granulats secs

Soit un mélange d'un granulat fin S et d'un granulat grossier G.

V

Le mélange est caractérisé par la proportion = [8]

SG

p

V V

+

SG SS

- Vss : volume absolu du granulat fin,

- VSG : volume absolu du granulat grossier.

Lorsqu'un récipient de volume VT est remplit d'un granulat, une partie de ce volume seulement est occupée par des grains solides (VS). L'autre partie reste vides (VV).

V

On désigne par indice des vides le rapport : e = [9]

V

V S 26

V_V

^m V V

+

SG SS

Ainsi l'indice des vides du mélange granulaire est :

e =

[10]

Chacun des granulats a son propre indice des vides : - e_S = indice des vides du granulat fin,

- e_G = indice des vides du granulat grossier.

Variation de l'indice des vides du mélange e_m en fonction de la proportion p - pour p = 0 (granulat fin seul), e_m = e S

- pour p = 1 (gros granulat seul), e_m = e_G

Pour simplifier le raisonnement, on suppose que V _SS + V_SG =1 (Unité) [11]

De ce fait on a :p=V_SG V _SS =(1-p) e_m =V_V

Si on démarre le mélange avec le granulat fin auquel on ajoute quelques grains du granulat grossier, les vides du mélange ne sont que les interstices entre les grains fins (fig. 16):

e _m =e _S ×V _SS =e _S ×(1-p) [12]

Si on part du gros granulat en ajoutant quelques grains du granulat fin, ces grains fins vont se loger dans les interstices laissés par les gros grains. Ainsi, le volume des vides du mélange est égal au volume des vides du gros granulat diminué du volume absolu du granulat fin (fig. 16) :

e e V V e p p p e

= × - = × - (1 - ) = × ( + 1) - 1 [13]

m G SG SS G G

[12] et [13] sont deux expressions différentes de variation de l'indice des vides suivant l'ordre dans lequel on mélange les deux types de granulat (Fig. 16.). Ainsi les deux hypothèses ne peuvent être vérifiées simultanément par un même mélange. Donc on ne peut pas conserver à la fois la structure du granulat fin et celle du granulat grossier. En réalité, il y a interaction entre ces deux structures définie par : l'effet de paroi et l'effet d'interférence (Gabrysiak, 2007).

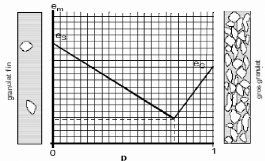
Fig. 16. - Evolution théorique de l'indice des vides d'un mélange granulaire (Gabrysiak,
2007)

27

2.2. - L'effet de paroi

Lorsqu'on détermine expérimentalement l'indice des vides du mélange de quelques grains du granulat grossier avec le granulat fin, on constate que cet indice est supérieur à ce que donnerait l'équation [12] (Fig. 20.). On a :

e_m=e_S×(1-p)+e_D×p [14]

A. Caquot (1937) in Gabrysiak (2007) interprète ce phénomène comme étant l'effet des parois des grains du gros granulat sur l'arrangement des grains du granulat fin.

En effet, dans toute section parallèle à la paroi, on peut définir un indice des vides local qui est le rapport entre l'aire des sections traversant des vides et l'aire des sections traversant des pleins. On observe que lorsqu'on se rapproche de la paroi, l'indice des vides local augmente et tend vers l'infini. Lorsqu'on s'éloigne de la paroi, l'indice des vides local tend vers l'indice des vides du mélange.

Ainsi, la présence de toute paroi (gros grain, peau de coffrage, armature, etc.) décompacte le granulat fin (Fig. 17.)

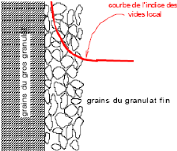
Fig. 17. - Effet de la paroi sur la compacité granulaire (Gabrysiak, 2007)

2.3. - L'effet d'interférence

Lorsque la proportion de gros granulats atteint un seuil de concentration, la manière dont ils sont disposés influe sur la compacité. En effet une partie des grains fins occupe les vides laissés par les gros grains. L'effet des parois des gros grains entraîne un décompactage des grains fins (fig. 18 et 19).

La disposition relative des parois des gros granulats détermine la forme et le volume des interstices dont dépend l'arrangement du granulat fin dans le mélange donc de son indice des vides. On parle ainsi d'interférence entre la structure du gros granulat et celle du granulat fin.

Fig. 18. - Disposition sans interférence Fig. 19. - Disposition avec interférence

28

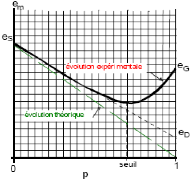
Fig. 20. - Evolution théorique et expérimentale de l'indice des vides du mélange granulaire
(Gabrysiak, 2007)

2.4. - Conclusion

Dans un mélange granulaire il y a généralement un effet de paroi et d'interférence du gros granulat sur le granulat fin. De ce fait, l'indice des vides du mélange ne peut pas être inférieur à une valeur minimale eD correspondant à une proportion optimale du gros granulat.

Ces différentes interactions, montrées théoriquement et expérimentalement visibles, ne sont pas facilement quantifiables. Cependant, lorsque le mélange comporte un granulat très fin, on admet la modélisation suivante (fig. 21) :

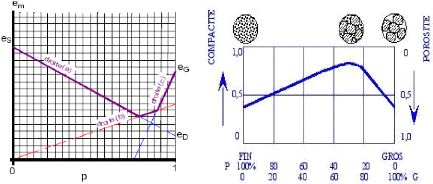
Fig. 21. - Modélisation de l'évolution de l'indice des vides (à gauche), de la compacité et de
la porosité (à droite) (Gabrysiak, 2007)

L'analyse de l'évolution de l'indice des vides montre :

Droite (a) : e_m = e S × (1 - p) + e_D × p Le mélange est riche en éléments fins, le gros granulat intervient par sa surface spécifique.

29

Droite (b) : e_m = k × p Le gros granulat intervient par la granulométrie de ses

interstices, donc à la fois par sa surface spécifique et son indice des vides. k est un coefficient qui a une signification physique complexe.

Droite (c) : e_m = (e_G -1) × p -1 Le mélange est pauvre en grains fins, le gros

granulat intervient par son indice des vides.

L'analyse de la variation de la compacité et de la porosité montre que la condition essentielle pour obtenir le moins de vides possible (meilleure compacité) dans un mélange de granulats fins et de granulats grossiers est: 35 % de fins et 65 % de grossiers.

Certains laboratoires corrigent par exemple la mesure de la masse volumique apparente ñ₀

afin de tenir compte de l'effet de paroi (grains/récipient).

Si la mesure est réalisée avec un récipient cylindrique, on a la correction suivante :

m

ñ₀ = Avec m = masse du granulat (g) et V = volume du récipient (cm³)

V

ñ₀

ñ [15]

1

,

= ⁰ 1 0 × S × D

V

ñ = masse volumique corrigée

S : surface intérieure du récipient y compris la face d'arasement (mm²) V : volume intérieur du récipient (mm³)

D : taille maximale du granulat (mm).

30

2ème Partie

Identification et Caractéristiques des matériaux

Evaluation de leur qualité

31