1. - Interaction entre les grains
Le contact de Hertz
Le contact non cohésif entre deux grains se compose
généralement d'une répulsion élastique normale N et
d'une résistance au glissement tangentielle T (fig. 3. (b)).
Le modèle de Hertz décrit le contact normal
entre deux grains purement élastiques, qui se déforment donc
lorsqu'ils sont soumis à une force (Chevoir, F., 2005 ; Ovarlez, G.,
2002 ; Roux et al, 2007). Dans le cas d'un contact entre deux
sphères, le calcul réalisé par Hertz en 1880 relie la
force de répulsion élastique normale au contact N à la
déflexion élastique h.
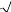
E a 3 / 2
[3]
3(1 í
a = Diamètre des grains
E = Module de Young (rapport entre la contrainte
normale et la déformation récupérée) í
= Coefficient de Poisson (rapport entre la déformation radiale et
la déformation axiale)
Le coefficient de frottement
Il y a dissipation plastique dès que la contrainte
tangentielle T est non nulle, ce qui conduit à des déformations
plastiques (Rognon, 2006). Ces déformations plastiques restent
limitées sur l'aire annulaire de contact tant que T est inférieur
au produit de l'effort normal aux billes N et du coefficient de frottement
tan?.
Quand T = Ntan? cette aire de
glissement s'étend à toute la surface de contact et un
déplacement apparaît entre les deux billes.
Cette description appelée loi de Coulomb
permet de décrire les phénomènes de déplacement et
d'écoulement granulaires.
Le coefficient de frottement tan? est lié
à l'état de surface des matériaux qui n'est jamais
parfaitement lisse : une rugosité existe à l'échelle
microscopique. Cette rugosité est à l'origine du frottement entre
les grains. Son effet est de favoriser une déformation plastique des
grains.
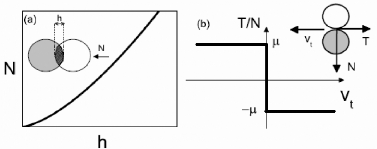
Fig. 3. - Loi de contact sans cohésion
: (a) contact de hertz décrivant la répulsion normale N
et (b)
critère de Coulomb simplifié décrivant le glissement
tangentiel (Rognon, 2006).
2. - Ecoulement des grains en cisaillement plan
homogène
Le cisaillement plan homogène est la
géométrie d'écoulement la plus simple pour décrire
les
caractéristiques du comportement rhéologique des grains
non cohésifs (Rognon, 2006). Elle
17
consiste à générer un écoulement
entre deux parois parallèles en exerçant une pression P,
ceci
en l'absence de gravité (fig. 4). Les résultats sont
obtenus par simulation numérique en
. V
imposant le taux de cisaillement H
ã et en mesurant la contrainte de
cisaillementô .
=
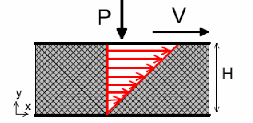
Fig. 4. - Géométrie
d'écoulement et forme du profil de vitesse en cisaillement plan
homogène
(Rognon, 2006)
2.1. - Les régimes
d'écoulement
Les simulations numériques menées par Cruz
(cité par Rognon, 2006) ont montré que le régime
d'écoulement des grains rigides de masse m est contrôlé par
un nombre sans dimension appelé nombre inertiel I.
L'expression de I dans un système à deux
dimensions est :
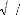
Ce nombre représente le rapport entre deux temps : le
temps inertiel m P et le temps lié au
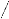
.
cisaillement 1 ã .
Les faibles valeurs de I (I = 1 0-3) correspondent
à un « régime quasi-statique » où l'inertie des
grains est négligeable. Le matériau a un comportement de type
solide plastique.
Les grandes valeurs de I (I = 0,3) correspondent à un
« régime collisionnel » où les grains interagissent par
collision binaire.
Entre ces deux régimes (10-2 = I = 0,3)
existe un régime d'écoulement appelé « régime
dense » où l'inertie des grains n'est pas négligeable. Le
réseau de contact percole à travers la cellule.
2.2. - Les lois de comportement
2.2.1. - Loi de frottement de Coulomb (u*)
Si la pression et le taux de cisaillement sont imposés,
il suffit de mesurer la contrainte de
cisaillement. La loi de comportement
des grains secs et sans cohésion peut s'écrire sous la
forme
d'une relation entre deux nombres sans dimension : le nombre inertiel I et le
coefficient
de frottement effectif u, rapport des contraintes tangentielle
et normale ì = ô P (fig. 5. (a)).
ì*=tan?+bI [5]
Cette relation est appelée « loi de frottement
».
L'angle de friction ? et la pente b > 0 sont propres
à la nature des grains en écoulement
18
2.2.2. - Loi de dilatance
Un paramètre fondamental dans les écoulements
granulaires est la fraction solide v (ou compacité) qui est le
rapport entre la surface occupée par les grains et la surface totale.
Elle dépend de l'état de cisaillement des grains (fig. 5.
(b)).
v = vmax - aI [6]
Cette relation est appelée « loi de dilatance
».
La compacité maximale vmax et la
pente a > 0 sont propres à la nature des grains en
écoulement.
Un empilement de grains initialement lâche se contracte
tandis qu'un empilement initialement dense se dilate
(désenchevêtrements).
Cependant, pour cisailler un matériau, il est
nécessaire que les grains passent les uns au dessus des autres (fig. 5.
(c)). Lorsque le nombre inertiel augmente, par augmentation du taux de
cisaillement ou par diminution de la pression, les
désenchevêtrements sont respectivement plus fréquents ou
plus faciles, ce qui conduit à l'expansion du matériau. Par
ailleurs, le
?
passage d'un grain par dessus un autre s'accompagne d'une
force N qui tend à s'opposer au mouvement (fig. 5. (c)) et qui
est à l'origine de l'augmentation du frottement avec le nombre
inertiel.
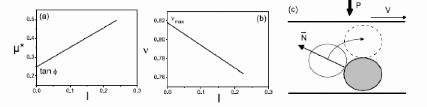
Fig. 5. - Comportement rhéologique de
grains sans cohésion : (a) loi de frottement, (b) loi de
dilatance,
(c) origine du frottement et de la dilatance (Rognon, 2006).
3. - Comportement expérimental des
matériaux granulaires 3.1. - Notion de résistance au
cisaillement
3.1.1. - Définition
Lorsqu'un système de forces est appliqué
à un volume déterminé d'un sol, il se développe en
général des contraintes de cisaillement entraînant des
déformations du sol. La résistance au cisaillement d'un sol est
définie comme étant la contrainte de cisaillement dans le plan de
rupture, au moment de celle-ci.
En effet, si on porte sur un graphique l'évolution de
la contrainte de cisaillement Z en
fonction de la
déformation s dans le plan de cette contrainte de cisaillement,
on obtient le
graphique indiqué par la figure 6. La résistance
au cisaillement est définie, sur ce graphique
comme étant le maximum de la contrainte de cisaillement
Zmax .
19
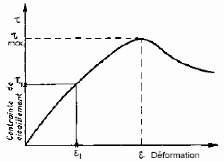
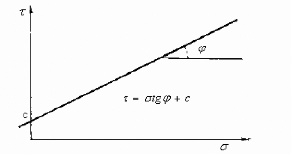
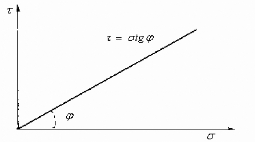
Fig. 6. - Courbe
contrainte-déformation
Ainsi, pour chaque système de
forces(ó,ô), on peut tracer à la rupture
un cercle de Mohr.
L'enveloppe des cercles de Mohr à la rupture est
appelée « courbe intrinsèque » (fig. 7.). Coulomb a
montré que la courbe intrinsèque des sols était une droite
d'équation :
ô=ó tg?+c [7]
- c a les dimensions d'une contrainte et
caractérise la « cohésion », - ? est
appelé « angle de frottement interne ».
Fig. 7. - Courbe intrinsèque d'un sol
fin
3.1.2. - Résistance au cisaillement des sols
pulvérulents
Les sols pulvérulents sont des sols sans cohésion
(c = 0). La théorie de Coulomb montre que la courbe intrinsèque
d'un tel type de sol est une droite passant par l'origine (fig. 8.):
ô=ó tg?
20
Fig. 8. - Courbe intrinsèque d'un sol
pulvérulent
La résistance au cisaillement d'un sol
pulvérulent est déterminée par la valeur de son angle de
frottement interne, qui dépend principalement de la compacité du
sol, de la forme et de l'état de surface des grains solides.
3.1.3. - Courbes contrainte-déformation d'un
matériau pulvérulent
Lorsqu'on effectue un essai de cisaillement direct sur un
matériau pulvérulent très compact on obtient (fig. 9.) la
courbe (1) présentant un maximum prononcé au-delà duquel
elle décroît de plus en plus lentement. Dans ce cas l'indice des
vides est faible car les grains sont enchevêtrés. Le maximum de la
courbe correspond à l'effort de cisaillement qu'il faut appliquer pour
provoquer le désenchevêtrement des grains dans le plan de
rupture.
Pour un sable lâche on obtient une courbe (2) ne
présentant pas de maximum. Elle croît de plus en plus lentement
pour tendre vers la courbe (1) dans le domaine des grandes déformations.
Dans ce cas le serrage des grains est lâche et au cours de l'essai le
volume initial de l'échantillon diminue.
Pour une valeur intermédiaire de l'indice des vides
appelée « indice des vides critique », l'essai se fait
à volume pratiquement constant. On obtient la courbe (3).
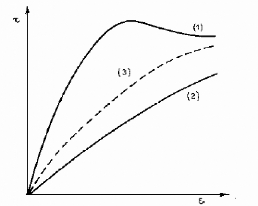
Fig. 9. - Courbe
contrainte-déformation d'un sol
pulvérulent
21
3.2. - Evaluation du comportement mécanique des
graves non traitées avec le triaxial à chargement
répété
Pour illustrer le comportement expérimental des
matériaux granulaires, on présentera les
résultats
d'essais triaxiaux réalisés par Bouvard et Stutz, (1982)
in Habiballah (2005) sur le
sable d'Hostun. Le chargement est
réalisé en exerçant simultanément une contrainte
de
confinement ó3 et une contrainte
axiale ó1 (donc une charge verticale q
appelée déviateur
des contraintes). Les déformations
axiale å1 et volumique åV
sont mesurées. Les résultats de
ces essais, typiques pour les matériaux granulaires sont
illustrés par la figure 10 (Gidel, 2001 ; Habiballah, 2005).
Les courbes de variation du déviateur des contraintes en
fonction de la déformation
axiale
q(å1) finissent par un palier qui
représente la plasticité parfaite. On observe également
une augmentation du déviateur de rupture avec la contrainte de
confinement.
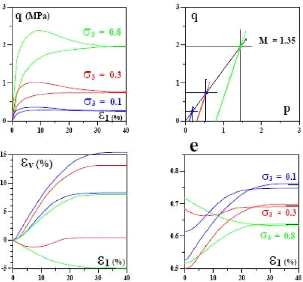
Fig. 10. - Essais triaxiaux sur le
sable d'Hostun [Bouvard (1982)] in Habiballah (2005).
Dans le plan
(p, q), les paliers de la plasticité parfaite se
trouvent sur une droite passant par
l'origine et de pente M qui correspond à l'angle de
frottement ?PP de plasticité parfaite, dans le plan
de Mohr.
q=ó1-ó3
p=
3
ó
1 + 2ó3
Les courbes de la variation volumique
e(å1) et å V
(å1) commencent toujours par une
contractance
volumique jusqu'à une déformation de å1
= 10-2 % environ. Cette phase de
22
au pic la courbe q(å1)
d'après la loi de Rowe (fig. 11). Cette pente diminue jusqu'à
0
correspondant à l'indice des vides critique ou à
l'état de plasticité parfaite. Dans cette phase, le
matériau se déforme sans variation de volume.
d V ou par l'angle de dilatanceø
.
å
d å 1
La dilatance est donc caractérisée par
tanâ =
Tant que l'état des contraintes reste en dessous de la
droite dans le plan (p, q), le matériau aura un comportement
contractant. Au-delà de cette droite, la compacité augmente et le
matériau se dilate.
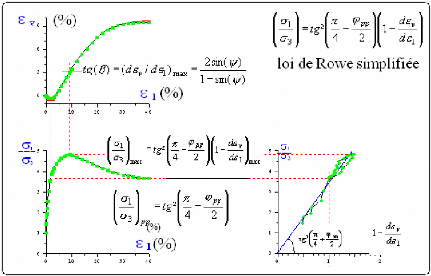
Fig. 11. - Visualisation de la dilatance dans
le plan de Rowe (ó 1/ó 3 ; 1-då v/då
1) in
Habiballah (2005)
3.3. - Conclusion
L'étude du comportement des matériaux granulaires
se fait en dissociant le comportement réversible (ou élastique)
du comportement irréversible (ou anélastique).
Le comportement d'un matériau granulaire est
considéré comme élastique linéaire pour des niveaux
de déformations faibles et plastique si les déformations
plastiques sont importantes. De ce fait le comportement est plutôt
élastoplastique.
Certains auteurs pensent que les matériaux granulaires
n'ont pas de domaine d'élasticité initial et que ce domaine est
créé seulement par écrouissage.
Dans un essai triaxial, les déformations permanentes
augmentent rapidement dès les premiers chargements. Elles se stabilisent
par la suite et le comportement devient pratiquement élastique.
Cependant, si les sollicitations sont trop élevées, les
déformations permanentes augmentent continuellement jusqu'à la
rupture éventuelle du matériau.
23



