e. Calcul des
armatures longitudinales comprimées et des armatures transversales
Figure 6.
Les formules ci-dessous nous aiderons à déterminer
les armatures longitudinales.
Au = 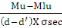 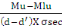 (B, 10) (B, 10)
Pour le moment limite ultime Mlu on a :
Mlu = MluX bo X d2 X Fbu
(B, 11)
Avec Mlu coefficient du moment
réduit ultime qui est de 0,300 (voir Béton I) .
äcoefficient de la hauteur ultime de la
poutre.
ä =  
Et d= 0,9h
d = 0,9 X 0,5
= 0,45
d'= 0,13 (théoriquement)
D'où ä =  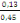
= 0,28
D'après (B, 11), nous avons :
Mlu =0,300X 0,20 X 0,452 X 14,16
= 0,172MPa
Le coefficient de moment fléchissant ?
est :
? = 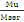 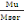 (B, 14) (B, 14)
Avec Mu le moment fléchissant ultime d'après (B, 4)
Mu = 653,66KN et Mser le moment ultime de service qui est :
Mser =  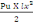
D'où Mser = 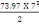 
= 453,06KN
(B, 14) devient :
? =  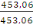
= 1
Contrainte d'équivalence des aciers comprimés   est : est :
  = valeur minimale [(9.?. fc28) - 0,9.
ä (13.25MPa + 415)] et 343MPa. = valeur minimale [(9.?. fc28) - 0,9.
ä (13.25MPa + 415)] et 343MPa.
D'où   = [(9 X 1 X 25) - 0,9 X 0,28 (13 X 25 + 415)] = [(9 X 1 X 25) - 0,9 X 0,28 (13 X 25 + 415)]
= 38,52MPa
Nous prenons   sec est 38,52MPa. sec est 38,52MPa.
D'après la relation (B, 10), nous avons :
Au =  
= 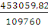 
= 5,45cm2
Par suite nous choisissons Au =
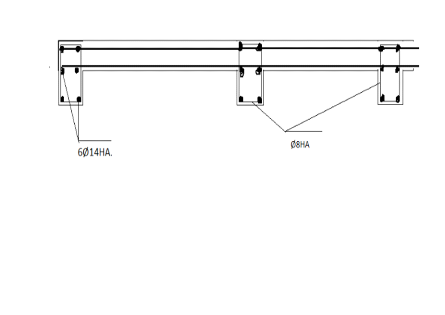
3,96cm2 qui nous donne 6Ø14HA.
f. Calcul des
aciers transversaux et de l'espacement maximum des armatures longitudinales
(St)
· Calcul des aciers transversaux
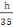 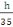
Ø transversale = valeur minimal Ø
long (B, 19)

D'où
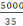 
Ø transversale = valeur minimal 12mm
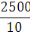
Ø transversale = valeur minimale entre 142,8mm, 12mm et
250mm.
Nous prenons la section de 8mm pour les armatures
transversales.
· Calcul de l'espacement maximum des armatures
longitudinales (St)
15 X Ø long
St = valeur minimale a + 10cm
(B, 20)
40cm
D'où
15 X 12mm
St = valeur minimale 25 + 10cm
(B, 20)
40cm
St = valeur minimale entre 18cm, 35cm et 40cm.
Nous prenonsl'espacement maximum des armatures longitudinales de
18cm.
Figure 7. Schéma de ferraillage de la
poutre
| 


