IV.2
DIMENSIONNEMENT DE LA POUTRE
a.
Généralité
Une poutre c'est une pièce en bois de forme
allongée, sevrant dans les constructions à supporter une
charpente ou un parquet. C'est aussi tout élément de construction
allongé en béton armé ou métallique qui joue le
rôle de supporter la dalle ou la toiture.
· Selon les matériaux, on distingue :
- La poutre en bois
- La poutre métallique
- La poutre en béton armé.
· Selon les matériaux, on distingue :
- La poutre principale
- La poutrelle
- La poutre croisée, c'est le cas général
qu'on rencontre dans la vie pratique.
Pour les calculs de poutre croisée, nous
procèderons en premier lieu à déterminer la
validité de la méthode dite simplifiée ou forfaitaire
à l'ELU.
Q1 =
5KN/m2 : charge d'exploitation sur la
G = 2
Q1 : poids propre de la dalle
(B, 1) 0,80 = (
 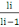 ) = 1,25 ) = 1,25
0,80 = (   ) = 1,25 ) = 1,25
F.P.P : fissuration peu
préjudiciable.
Dans notre projet la poutre la plus vulnérable a une
portée de 800cm et elle est représentée sur la figure
ci-dessous.
Figure 5.

b. Pré
dimensionnement de la poutre
Le pré dimensionnement de la poutre s'effectue à
l'aide des formules suivantes :
  lt = h = lt = h =   lt (B, 2) lt (B, 2)
0,4h =bo= 0,5h (B, 3)
· D'après (B, 2), nous déterminons la hauteur
h de la poutre.
On a:   8m= h = 8m= h =  8m 8m
D'où 0,5m =h = 0,66m
Nous prenons h = 0,5m.
· D'après (B, 3), nous déterminons la base bo
de la poutre.
On a: 0, 4 X 0, 5 = bo= 0,5 X 0,5
D'ou 0,20m =bo= 0,25m
Nous prenons bo = 0,20m.
c.
Évaluation et combinaison de charges
La poutre subie deux charges dont charge d'exploitation Q et les
charges permanentes G en conservant la relation (A, 3)
· Charges permanentes G :
ü Poids propre de la poutre :   = 2,55KN/m = 2,55KN/m
ü Poids de revêtement : 20 X
0,03 X 7 = 4,2 KN/m
ü Poids de la dalle : 5,05 X
7 = 35,35 KN/m
D'où G = 2,55 +4,2 + 35,35 = 42,1KN/m2
· Charge d'exploitation Q :
La surcharge d'exploitation Q pour la dalle est Q = 2,5 X 7 =
17,5KN/m2
D'après (A, 3) la charge pondéré Pu
est :
Pu = (1,35 X 42, 1) + (1,5 X 17,5)
= 73,97 KN/m2
d. Calcul des
sollicitations
Dans cette poutre nous calculons les moments en travée de
rive et en travée intermédiaire et puis la vérification de
moment fléchissant.
· Les moments fléchissant en travée de
riveMa,w
Les moments fléchissant en travée de rive
Ma,w est donné par la relation :
On aMa,w = 0,6 X
MOi(B, 4)
Avec MOi= 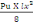 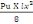
= 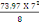
= 453,06 KN
D'oùMa,w = 0,6 X 453,06
= 271,80KNm
· Les moments fléchissant en travée
intermédiaireMa,e
On sait que : Ma,e = 0,6 X
MOi.  (B, 5) (B, 5)
D'oùMa,e =
0,6 X 453,06 X  
= 135,91KN
· Le moment fléchissant en travée de rive
à plusieurs travées intermédiaires
Mti obtenu par l'équation :
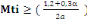 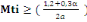 (B, 6) (B, 6)
Avec   le coefficient des charges qui est obtenu par la relation : le coefficient des charges qui est obtenu par la relation :
  = = 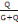 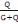 (B, 7) (B, 7)
= 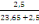 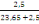
  = 0,087 = 0,087
D'après (B, 6), on a :
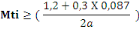
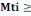 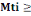 277,72KN 277,72KN
Nous prenonsMti= 400KN
· Vérification des moments
fléchissant
Pour la vérification des moments fléchissant nous
avons la relation :
(1 + 0,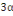  )MOi )MOi
Mti +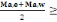 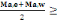 valeur max (B, 8) valeur max (B, 8)
1,05MOi
D'une part : Mti +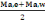 
= 400 +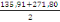 
= 603,85 KN
D'autre part : (1 + 0,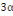 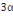 )MOi )MOi
1,05MOi
(1 + 0, 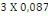 ) 453,06 ) 453,06
1,05X 453,06
La valeur maximale entre 464,88 KN et 475,71 KN est 475,71 KN.
De ce qui est ci-dessus nous remarquons que : 603,85 KN =
475,71 KN.
· Les efforts tranchants sur les appuis
L'effort tranchantVuiest donné par la
relation :
Vui= 1,15(Vox) (B, 9)
Avec Vox= (  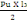 ) )
On a = ( 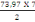 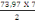 ) )
= 258,89 KN
D'après (B, 9), Vuidevient :
Vui= 1,15 X 258,89
= 297,72 KN
| 


