IV.3
DIMENSIONNEMENT DE POTEAU
a.
Généralité
Figure 8.
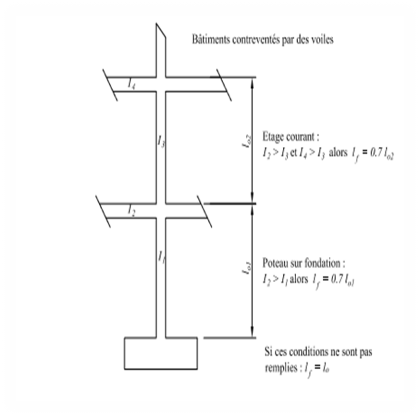
Un poteau est une poutre verticale soumise uniquement à
une compression centrée (Nu ? 0 et Mz
= 0)
Il joue le rôle de répartition des charges
Nu la fondation.
Un poteau de section rectangulaire ou approcher et à forme
non allonger en plan s'appelle pilier.
Un poteau de section circulaire ou approcher sera appelé
colonne.
Un poteau de section parallélépipédique sera
appelé poutre.
Du point de vue de la mécanique de la structure, les
poteaux sont les éléments verticaux soumis principalement
à la compression et leur résistance est notamment limitée
par le risque de flambement.
b. Pré
dimensionnement en compression simple de poteau le plus défavorable
La longueur libre entre haut du plancher supérieur et la
fondation vaut Lo = 3cm.
Le poteau est traversé de part et d'autre par une poutre
ayant une section de 20 X 50cm.
Sa longueur de flambement vaut :
Lfl = 0,5Lo (C, 1)
On a Lfl = 0,5 X 3
= 1,5m
L'élancement ë
Figure 9. Y
B
X
25cm
Nous calculons l'élancement ë par la
relation :
ë 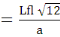  = 35(C, 2) = 35(C, 2)
Avec a, le coté du carré voire la
figure 9 on a :
ë  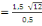
  6 X 3,46 6 X 3,46
D'où ë = 26,76m = 35
c. Descente des
charges
La descente de charges est donnée par la
relation :
 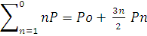 (C, 3) (C, 3)
Figure 10.
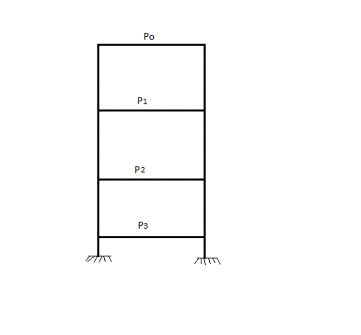
La surface d'influence S est de 16 X 48 =
768m2.
Avec Po la charge de toiture qui est :
Po = 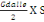 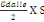 (C, 3) (C, 3)
On a Po= 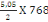 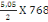
= 1939,2KN
Et P1 la charge du niveau de
référence.
On a P1 = charge dalle + charge
poutre
= 9,06 + 73,97
= 83,03KN
D'où (C, 3) devient :
Niveau 0
On a No = Po + 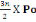 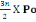
= 1939,2+  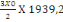
= 1939,2KN
Niveau 1
On a N1 = Po +  
= 1939, 2+  
= 2063, 74KN
Niveau 2
On a N2 = Po +   et et  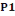 = = 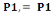
= 1939,2+ 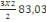 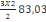
= 2188,29KN
d. Combinaisons des
charges
Les charges qui agissent sur le poteau sont obtenues en combinant
la charge dalle, celle de toiture et des niveaux considères.
On a Nu=
N0+N1
+N2
= 1939,2+2063,74+2188,29
= 6191,23NK
· La section réduite Br
Nous avons un poteau carré de 25 x 25
D'où Br = 625cm2
· Calcul de force équilibrée par le
béton Nb
On a Nb = 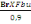 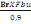 (C, 4) (C, 4)
Avec fbu=14,16MPa
D'où Nb =  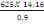
= 983,3KN
· Calcul de force équilibréedes
armatures longitudinalesNS
On a NS = 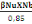  (C, 5) (C, 5)
Avec  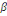 =1 + 0,2( =1 + 0,2(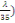  2 (C, 6) 2 (C, 6)
=1 + 0,2(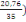  2 2
= 1,07
D'où (C, 5) devient :
NS = 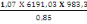 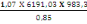
= 6636,84KN
e. Calcul des
armatures longitudinales et transversales
| 


