2. Estimation du modèle
On procède à l'estimation des dix processus
précédemment identifiés. Le résultat de ses
estimations nous est présenté dans le tableau
ci-dessous :
Tableau 5: résultats des estimations des
coefficients des modèles
|
Coefficients
|
Modèle 1
|
Modèle 2
|
Modèle3
|
Modèle 4
|
Modèle 5
|
|
ARIMA(1,1,0)
|
ARIMA (2,1,0)
|
ARIMA (0,1,1)
|
ARIMA(1,1,1)
|
ARIMA(2,1,1)
|
|
Dpibt
|
-
|
-
|
-
|
-
|
-
|
|
Dfbc
|
-
|
-
|
-
|
-
|
-
|
|
C
|
0,059*
(0,048)
|
0,056*
(0,020)
|
0,056*
(0,047)
|
0,053*
(0,023)
|
0,056*
(0,050)
|
|
AR
|
0,066
(0,643)
|
-0,019
(0,941)
|
-
|
0,839
(0,000)
|
-0,021
(0,943)
|
|
MA
|
-
|
-
|
0,070
(0,619)
|
-1,000
(0,999)
|
0,069
(0,651)
|
|
0,0045
|
0,0003
|
0,0047
|
0,0815
|
0,0052
|
|
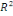 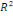 ajusté ajusté
|
-0,0558
|
-0,0601
|
-0,0555
|
-0,0045
|
-0,0879
|
|
Erreur standard
|
0,1357
|
0,1360
|
-0,1357
|
0,1324
|
0,1377
|
|
Somme des carrés de résidus
|
0,6080
|
0,6105
|
0,6079
|
0,5610
|
0,6076
|
|
Log vraisemblance
|
22,3740
|
22,3013
|
22,3781
|
23,1140
|
22,3868
|
|
Mean dependent var
|
0,05653
|
0,0564
|
0,0565
|
0,0565
|
0,0565
|
|
S.D.dependent var
|
0,1321
|
0,1321
|
0,1321
|
0,1321
|
0,1321
|
|
AIC
|
-1,0763
|
-1,0722
|
-1,0765
|
-0,6189
|
-1,0214
|
|
SC
|
-0,9443
|
-0,9403
|
-0,9446
|
-0,8859
|
-0,8455
|
Tableau 6 : résultats des estimations des
coefficients des modèles (suite)
|
Coefficients
|
Modèle 6
|
Modèle 7
|
Modèle 8
|
Modèle 9
|
Modèle 10
|
|
ARIMAX(1, 1,0)
|
ARIMAX(2, 1,0)
|
ARIMAX(0, 1,1)
|
ARIMAX (1, 1,1)
|
ARIMAX(2, 1,1)
|
|
Dlpibt
|
1,063*
(0,000)
|
0,986*
(0,000)
|
1,075*
(0,000)
|
1,081*
(0,000)
|
1,076*
(0,000)
|
|
Dfbc
|
0,009*
(0,010)
|
0,009*
(0,054)
|
0,008*
(0,0149)
|
0,007*
(0,024)
|
0,007*
(0,017)
|
|
C
|
0,013
(0,169)
|
0,017
(0,230)
|
0,011*
(0,013)
|
0,011*
(0,023)
|
0,011*
(0,015)
|
|
AR
|
-0,446*
(0,012)
|
-0,107
(0,690)
|
-
|
-0,063
(0,812)
|
-0,086
(0,715)
|
|
MA
|
-
|
-
|
-0,694*
(0,000)
|
-0,660*
(0,000)
|
-0,661*
(0,007)
|
|
Sigma
|
0,005*
(0,000)
|
0,006*
(0,003)
|
0,004*
(0,000)
|
0,004*
(0,000)
|
0,004*
(0,000)
|
|
0,69326
|
0,6234
|
0,745358*
|
0,7458*
|
0,7467
|
|
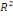 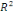 ajusté ajusté
|
0,6536
|
0,5748
|
0,7125*
|
0,7034
|
0,704564
|
|
Erreur standard
|
0,0777
|
0,0861
|
0,0708*
|
0,0719
|
0,071805
|
|
Somme des carrés de résidus
|
0,1873
|
0,2300
|
0,1555*
|
0,1552
|
0,154678
|
|
Log vraisemblance
|
43,4555
|
39,862
|
46,588*
|
46,62062
|
46,6849*
|
|
Mean dependent var
|
0,0565*
|
0,0565*
|
0,0565*
|
0,0565*
|
0,05653*
|
|
S.D.dependent var
|
0,1321*
|
0,1321*
|
0,1321*
|
0,1321*
|
0,1321*
|
|
AIC
|
-2,1364
|
-1,9368
|
-2,3104*
|
-2,2567
|
-2,260275
|
|
SC
|
-1,9164
|
-1,7168
|
-2,2336*
|
-1,9927
|
-1,996355
|
Note :* indique la significativité au seuil de
5%. Les valeurs entre parenthèses sont les p-values.
Source : nos calculs sur Eviews 9
Ayant tous ses coefficients significatifs hormis pour les
variables INF et DU ; avec unesignificativité globale la plus
élevée (R² ajusté = 0,71), des critères
d'informations (AIC= -2,310 et SC= -2,233) minimum, le modèle ARIMAX (0,
1,1) donne de flair des bons résultats. En conséquence, à
l'issue de l'étape d'estimation, seul le modèle ARIMAX (0, 1,1)
est apte à la prévision des recettes fiscales.
3. Validation du modèle
ü Correlogramme des résidus
Tableau 7 : Corrélogramme des
résidus
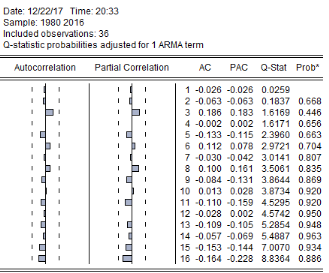
Source : nos calculs sur Eviews 9
De manière visuelle, nous constatons qu'aucun pic n'est
à l'extérieur des deux intervalles de confiance. D'où les
résidus se trouvent à l'intérieur de l'intervalle de
confiance. De plus, la probabilité des Q-stat est proche de 1 ce qui
signifie quele résidu peut être assimilé à un bruit
blanc, le modèle est validé et peut être
représenté par ARIMAX (0, 1,1).
ü Test de Breusch-Godfrey pour
l'autocorrélation
La détection de l'autocorrélation par le
processus Breusch-Godfrey se fait avec comme hypothèse :
· H0 : absence d'autocorrélation
· H1 : présence d'autocorrélation
Tableau 8 : test d'autocorrélation de
Breusch-Goldfrey
|
Heteroskedasticity Test Breusch-Pagan-Godlfrey
|
|
F-statistic
|
0.232
|
Prob. F(2,33)
|
0,726
|
|
Obs*R-squared
|
0,691
|
Pro. Chi-Square
|
0,707
|
|
Scaled explained
|
0,498
|
Prob-Square
|
0,779
|
Source : nos calculs sur Eviews 9
La probabilité calculée est supérieure
à la probabilité critique de 5%, on accepte H0. Il ya donc
absence d'autocorrélation des erreurs.
ü Test
d'hétéroscédasticité d'ARCH
La détection de
l'hétéroscédasticité par le processus de white se
fait avec comme hypothèse :
· H0 : il ya homoscédasticité
· H1 : il ya
hétéroscédasticité
Les résultats du test d'ARCH où 2 est le retard
optimal, sont reportés dans le tableau suivant :
Tableau 9 : test
d'hétéroscédasticité d'ARCH des
résidus
|
Heteroskedasticity test ARCH
|
|
|
F-stat
|
0,607
|
Prob.F(2,31)
|
0,551
|
|
Obs*R-squared
|
1,282
|
Prob.Chi-Square(2)
|
0,526
|
|
Source : nos calculs sur Eviews 9
La probabilité calculée est supérieure
à 5% donc on accepte l'hypothèse nulle. Le modèle est
homoscédastique.
ü Test de normalité
Graphique 10: test de normalité des
résidus
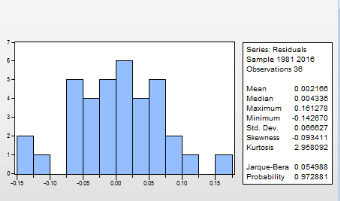
Source : nos calculs sur Eviews 9
Le test de normalité de Jarque-Bera est un test
d'hypothèse qui cherche à déterminer que les
données suivent une loi normale. Ce test est fondé sur les
coefficients d'asymétrie et d'aplatissement. Pour appliquerce test, nous
allons dans un premier temps procéder au calcul du coefficient
d'asymétrie de Skewness et celui d'aplatissement de Kurtosis puis dans
un second temps à comparer sa probabilité au khi deux avec 2
comme degré de liberté
· Pour Skewness

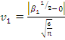 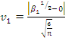 (26) (26)
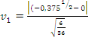 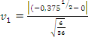 (26.1) (26.1)
Selon l'histogramme 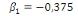 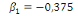 et n (le nombre d'observation) est égale à 36. Par
conséquent : et n (le nombre d'observation) est égale à 36. Par
conséquent :
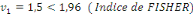
On accepte donc l'hypothèse 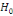 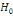 la distribution des résidus est symétrique la distribution des résidus est symétrique
· Pour Kurtosis :
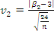 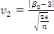 (27) (27)
 
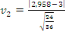 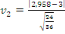 (27.1) (27.1)
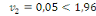 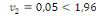 (Indice de FISHER) (Indice de FISHER)
On accepte l'hypothèse nulle dont la distribution est
relativement aplatie.
Tableau 10: Résultat du test de
normalité des résidus du modèle
|
Test
|
Khi deux
|
Probabilité
|
|
Jarque-Bera
|
0,5
|
0,97
|
Source : nos calculs sur Eviews 9
Comme la probabilité critique (0,97) est
supérieure à 0,05, on peut en conclure que les résidus du
modèle ARIMAX (0, 1,1) Suivent une loi normale.
Notre modélisation par la méthode Box et Jenkins
de la série des recettes fiscales est donc représenté par
ARIMAX (0,1, 1).
|
|



