1.2. Détermination du nombre de
retard
Pour effectuer ce travail, nous allons utiliser les tests
suivants :
· d'Akaike (AIC)
· maximum de vraisemblance (LR)
· Scharz (SC)
· Hannan-Quinn (HQ)
· Final de prédiction des erreurs (FPE)
Concernant les tests de d'Akaike (AIC), Scharz (SC) et celui
de hannan-quinn, le retard optimal est celui qui minimise le critère du
test, tandis que pour le test du maximum de vraisemblance (LR), ce retard
maximise la log-vraisemblance. Les résultats
Obtenus sont les suivants :
Tableau 4 : Détermination du retard
optimal
|
Lag
|
Log L
|
LR
|
FPE
|
AIC
|
SC
|
HQ
|
|
0
|
-595 ,7950
|
NA
|
2,47e+10
|
35,28206
|
35,46163
|
35,34330
|
|
1
|
-370,3937
|
384,5082
|
111459,9
|
22,96434
|
23,86219 *
|
23,27053
|
|
2
|
-344,7217
|
37,75296 *
|
65876,42 *
|
22,39539 *
|
24,01154
|
22,94655 *
|
|
3
|
-332,5117
|
15,08288
|
92088,65
|
22,61834
|
24,95277
|
23,41445
|
Note : *indique l'ordre du retard
sélectionné par les critères considérés.
(Chaque test est au seuil de 5%)LR : le rapport de vraisemblance ;
AIC : Critère d'Akaike ; SC : Critère de
Schwarz ; HQ : critère d'Hannan-Quinn ; FPE : Erreur
de Prédiction Final.
Source : nos calculs sur Eviews 9
Ces résultats montrent qu'à p=2, les
critères d'information AIC, HQ et FPE sont minimisés à
l'exception du test de SC pour lequel celui-ci est égal à 1. Dans
la suite de notre analyse il ressort clairement que le retard optimal est
égal à 2 (p=2).
Le retard optimal étant connu, nous pouvons passer
à l'analyse du corrélogramme.
1.3. Analyse du corrélogramme
La série étant stationnaire en différence
première, on recherche un modèle ARIMA (p, d, q) ou ARIMAX (p, d,
q) qui représente au mieux notre série. Pour ce faire, on examine
les autocorrélations simples (pour la détermination de retards de
MA) et les autocorrélations partielles (pour déterminer le nombre
de retard d'un processus AR).
Graphique 9 :
corrélogramme de la série Log RF (-1)
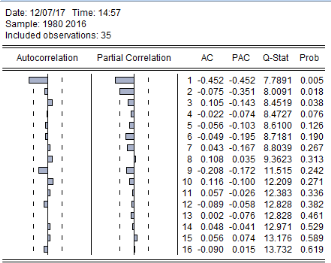
Source : nos calculs sur Eviews 9
En analysant ce corrélogramme on en déduit
que seules les deux premières fonctions d'auto corrélation
et la première fonction d'auto corrélation partielle sont
significativement différentes de zéro.Les modèles
adéquats sont : ARIMA(1, 1,0) ; ARIMA(2, 1,0) ; ARIMA(0,
1,1). ARIMA (1, 1,1) et ARIMA (2, 1,1). Aussi en prenant en compte des
variables exogènes nous obtenons les modèles :
ARIMX(1, 1,0) ; ARIMAX(2, 1,0) ; ARIMAX(0,
1,1) ; ARIMAX (1, 1,1) et ARIMAX (2, 1,1).
| 


