I. Présentation des résultats
1. La phase d'identification d'un modèle
préliminaire
1.1. Résultat des tests de
stationnarité
Les données étant annuelles, notre
démarche visera à vérifier si la variance, la moyenne et
l'espérance de la série des recettes fiscales ainsi que celles
des autres variables dont porte notre analyse, restent stables (invariants)
pour tout changement de l'origine du temps, en vue de garantir une bonne
régression. D'où la notion de stationnarité ou de
non-stationnarité. Pour se faire, plusieurs tests peuvent être
utilisés :
· Test de Dickey Fuller Augmenté (ADF)
· Test de Kwiatkowski-Phillips-Schmidt-Shin (KPSS)
· Test de Phillips-perron (PP)
Pour notre étude, nous utiliserons le test ADF et PP
qui consiste :
· H0 : la série n'est pas stationnaire
· H1 : la série est stationnaire
NB : les variables tels que les recettes fiscales et le
produit intérieur brut par tête ont été
générées en logarithme pour réduire
l'échelle de variation des données.
Les résultats de ces différents tests se
trouvent dans le tableau suivant :
Tableau 2 : Résultat des tests de
stationnarité sur les variables
|
Variables
|
Niveau
ADF PP
|
Différence première
ADF PP
|
Différence seconde
ADF PP
|
|
LOG (Recettes fiscales)
|
2,5953
(0,9970)
|
-1,8641
(0,6521)
|
-5,775 **
(0,0004)
|
-5,4775 **
(0,0004)
|
-6,7508**
(0,000)
|
-17,1346**
(0,000)
|
|
LOG (PIB par tête)
|
2,7605
(0,9980)
|
2,2901
(0,9925)
|
-4,2532 **
(0,0098)
|
-4,2232 **
(0,0105)
|
-7,8860**
(0,000)
|
-8,0704**
(0,000)
|
|
Degré d'urbanisation
|
1,630
(0,9725)
|
9,0007
(1,000)
|
-1,2530
(0,6396)
|
-1,2530
(0,6396)
|
-4,0964**
(0,0146)
|
-3,8842**
(0,0238)
|
|
Formation brute de capital fixe
|
-2,8155
(0,0661)
|
-2,7935
(0,0692)
|
-7,4174 **
(0,000)
|
-7,5210 **
(0,000)
|
-7,5820 **
(0,000)
|
-24,3239**
(0,000)
|
|
Indice des prix à la consommation
|
-0,2312
(0,9253)
|
-0,2582
(0,9214)
|
-4 ,4863 **
(0,0055)
|
-4,4863 **
(0,0055)
|
-6,8327**
(0,000)
|
-11,5366**
(0,000)
|
Note : * indique le rejet de l'hypothèse nulle
pour le seuil de 5%.
** indique le rejet de
l'hypothèse nulle pour le seuil de 10%
Source : nos calculs sur Eviews 9
Les résultats des différents tests indiquent que
les séries ne sont pas stationnaires en niveau au seuil de 5% car chaque
variable, que ce soit le test de Dickey-Fuller Augmenté (ADF) ou le test
de Phillips-Perron (PP), la statistique du test est inferieure en valeur
à la valeur critique pour chaque variable.
Les variables n'étant pas stationnaires en niveau,
notre démarche consistera à les différencier
(intégrer). Les variables différenciées sont donc
notées : D(lpibt), D(du), D(lrf), D(fbcf) et D(ipc).
Les résultats des différents tests indiquent que
toutes les variables sont stationnaires en différences premières
(intégrées d'ordre 1) car les statistiques des tests sont
supérieures en valeurs absolue à la valeur critique au seuil de
5% excepté la série (du). La variable (du) en différence
seconde est stationnaire, car que ce soit le test de Dickey-Fuller
Augmenté (ADF) ou le test de Phillips-Perron (PP), la statistique du
test est inferieure en valeur à la valeur critique pour de la
variable.
Ainsi, le résultat définitif est consigné
dans le tableau ci-dessous.
Tableau 3 : récapitulatif des tests de
stationnarité sur les variables
|
Variables
|
Test Dickey-Fuller
|
Test PP
|
|
Log (Produit Intérieur Brut par
tête)
|
I(1)
|
I(1)
|
|
Formation brut de capital fixe
|
I(1)
|
I(1)
|
|
Degré d'urbanisation
|
I(2)
|
I(2)
|
|
Log (recettes fiscales)
|
I(1)
|
I(1)
|
|
Indice de prix à la consommation
|
I(1)
|
I(1)
|
Source : nos calculs sur Eviews
Ce tableau montre que toutes les variables sont stationnaires
en différence première (elles sont marquées I(1)) pour
les tests d'ADF et de PP, excepté le degré d'urbanisation qui est
stationnaire en différence seconde (la variable est marquée
I(2)). Dans la suite de notre étude, il ressort clairement que toutes
les variables sont stationnaires en différence première.
Graphique 8: la série Log RF (-1)
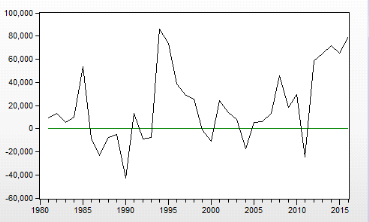
Source : nos calculs sue Eviews 9
Par analyse visuelle, on peut conclure que la série est
stationnaire car elle tourne autour de sa moyenne.
|
|



