3. Les processus stationnaires
L'étude de la stationnarité est indispensable
pour la validité d'une régression sur les séries
chronologiques.
Un processus est stationnaire lorsqu'il ne comporte ni
tendance, ni saisonnalité. C'est-à-dire que sa moyenne, sa
variance et sa covariance restent invariantes au cours du temps.
On a donc :
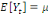 ü ü 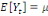 Pour tout t Pour tout t
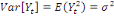 ü ü 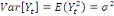 , pour tout t , pour tout t
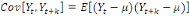 ü ü 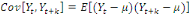
Par opposition, un processus non-stationnaire est un processus
dont la moyenne et la variance varient. Pour l'étude d'une série
chronologique telle que la série des recettes fiscales, il est
conseillé de travailler avec une série stationnaire. De prime
abord, on fera des tests de stationnarité tels que le test
de Dickey-Fuller (DF), le test de Dickey-Fuller Augmenté (ADF), le
test de Phillips-Perron (pp), le test de Schmidts-Phillips, le test
d'Eloitt-Rothenberg-Stock (ERS) et celui de KPSS, pour voir si la série
est stationnaire ou non-stationnaire.si après le test, il en ressort que
la série est non-stationnaire, on cherchera donc le type du processus.
On en distingue deux types :
ü Le processus TS (Trend Stationnary)
ü Le processus DS (Differency Stationnary)
3.1. Le processus TS (Trend Stationnary)
Appelé en français processus Tendance
Stationnaire, sa formule générale est :
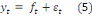
Ce processus peut aussi s'écrire de façon
suivante :
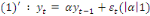
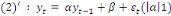
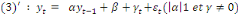
3.2.Le processus DS
(Différence stationary)
Appelé en français Différence
Stationnaire, sa formule est :
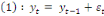
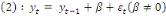
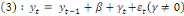
1.1. Différenciation
La différenciation ou intégration, qui consiste
à ôter la tendance dans notre série chronologique.
D'oùon aura :
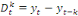 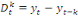 (6) (6)
Ainsi si la série chronologique est notée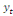 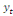 , on aura : , on aura :
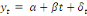 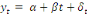 (7) (7)
Si nous sommes à la première intégration
(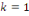 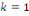 ), l'équation (6) devient : ), l'équation (6) devient :
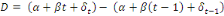 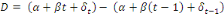 (6.1) (6.1)
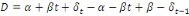 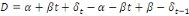 (6.1) (6.1)
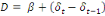 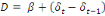 (8) (8)
| 


