III-10. Modèle du bus continue
L'évolution de la tension du bus continu est
donnée par la formules suivantes :
??0+????
1 (III.28)
??????(??) = ???? ? 1 ?? ????(??)???? + ????(??0)
??0
59
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
Avec :
?? : La capacité du bus continu D'après
la loi des mailles on a :
(III.29)
'dc = '????d + 'c
'c = 'dc - '????d Donc :
????dc
(III.30)
'c = ?? ????
III.5.3 Modélisation du convertisseur
cotée réseau
L'onduleur de tension est un composant de
l'électronique de puissance qui converti une tension continue
d'entrée en une tension de sortie alternative, il est composé de
six interrupteurs bidirectionnels qui son constitué d'un transistor et
de diode de roue libre qui sert à protéger des thyristors.
(Figure III.11), les interrupteur (K1,K4);(K2,K5);(K3,K6) son
complémentaire c-à-d quand l'un est ouvert l'autre doit
être fermée afin d'éviter les courts-circuits delà
source. Afin d'éviter, il est aussi impérativement
nécessaire d'espacé le temps de fermeture de T21 ; T22 ou T23 et
le temps d'ouverture de T11, T12, T13 et vice versa.
Afin de modéliser l'onduleur de tension on peut
considérer le circuit comme étant l'association de trois
onduleurs monophasés en demi-point aussi la source continue
peut-être
décomposée en deux sources équivalentes de
tension (??????
2 ) avec un point milieu fictif « O
».Pour
simplifier l'étude, on supposera que :
· La commutation des interrupteurs est
instantanée,
· Les chutes de tension à leurs bornes sont
négligeables,
· La charge est triphasée équilibrée
et couplée en étoile avec point neutre isolé « n
».
60
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
VCA
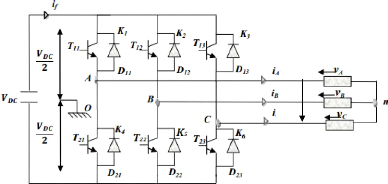
Figure III-11. Onduleur de tension triphasée
[22]
Le système triphasé obtenu à la sortie de
l'onduleur est équilibré en tension, ne contenant que les
harmoniques impairs différents de trois, les harmoniques de rang trois
et multiples de trois étant éliminés.
On peut exprimer les tensions composées par :
{
VAB = VAO - VBO (III.31)
VBC = VBO - VCO
VCA = VCO - VAO
· Au niveau de la charge, on peut déduire les
relations donnant les équations des tensions simples son donné
par l'équation III .32 :
{
VAB = VA - VB
(III.32)
VBC=VB - VC VCA=VC - VA
En effectuant les différences (VAB -
VCA), (VBC - VAB), (VCA -
VBC) membres à membres on trouve :
{
VAB - VCA = 2 VA - (VB + VC
(III.33)
VBC - VAB = 2 VB - (VA + VC) VCA -
VBC = 2 VC - (VA + VB)
On a un système équilibré donc on
déduit que :
61
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
(III.34)
{
??????- ?????? = 3 ???? ?????? - ??????= 3 ???? ?????? - ??????
= 3 ????
Donc :
1 (?????? - ??????) 3
???? =
???? =
|
1 (??????- ??????) 3
|
(III.34)
|
|
???? =
1 (?????? - ??????) 3
L'expression des tensions simples liant les tensions
mesurées entre les points A, B, C et le point milieu O est
définie par :
???? 1 2
???? = -1
???? 3 -1
-1
2
-1
|
-1
-1
2
|
?????? ]
??????
??????
|
(III.35)
|
|
L'état des interrupteurs, supposés parfaits peut
être définit par trois grandeurs booléennes de commande
????(i =A, B, C) :
· ????=1, alors les interrupteurs du haut sont
fermée (passant) et les interrupteurs du bas sont
ouvert(bloquée).
· ????=0, alors les interrupteurs du haut son ouvert
(bloquée) et les interrupteurs du bas son fermée (passant).
· Cela nous permet d'écrire l'équation
III.36 :
?????? ?????? ???? (III.36)
?????? = ????
?????? 2 ????
Donc :
???? ???? 2 -1 -1 (III.37)
] . 1
[ ???? ] = [ ???? ] . ?????? -1 2 -1
2 . [ 3
???? ???? -1 -1 2
III.5.4 Modélisation du filtre
Pour l'atténuation des harmoniques de courant un filtre
triphasé est utilisé reliant le convertisseur cote réseau
à ce dernier.
62
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
L'architecture du filtre est représentée à
travers la figure III.12.
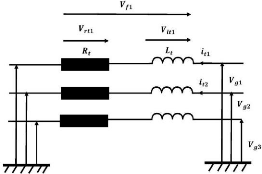
Figure III-12. Filtre coté réseau.
Les courants dans le filtre supposé sinusoïdal
équilibré sont donnés par :
??0+????
1
????1(??) = ? ??????1???? + ????1(??0)
????
??0
??0+????
????2(??) = 1 ? ??????2???? + ????2(??0)
???? ??0
????3(??) = -(????1 + ????2)
|
(III.38)
|
|
Les tensions aux du filtre s'écrivent :
{
????1 = ????1 - ????1 - ??????1
(III.39)
????2 = ????2 - ????2 - ??????2
Avec :
{
??????1 = ????????1 (III.40)
????2 =
????????2 De suite la définition des vecteurs ????, ???? et ???? :
???? =
(????1 (III.41)
) ????2

=
??
??1 )?? ??2

???? = (????1)
????2
??(??
(III.42)
(III.43)
63
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
III.5.5 Commandes à Modulation de Largeur
d'Impulsion (MLI)
Afin de déterminer les signaux délivrés
par l'onduleur il est impérativement nécessaire de
commandée les grandeurs ????, ????, et ???? par une commande
spécifique parmi ces commandes il existe une commande appelée
commandes à Modulation de Largeur d'Impulsion (MLI) [35].
Il existe plusieurs types de commande MLI chaque
méthode est différente de l'autre par apport à leurs
principes et leurs méthode employée parmi les principales
stratégie MLI on cite quelqu'une :
· La MLI Sinus-Triangle (à échantillonnage
naturel)
· Les MLI à échantillonnage
régulier
· La MLI vectorielle
· La MLI suboptimale
· La MLI précalculée ou calculée
Nous allons nous intéresser principalement dans ce
paragraphe est la MLI Sinus-Triangles. III.5.5.1 Modulation a largeur
d'Impulsion Sinus-Triangle
La commande MLI "Sinus-Triangle", dite à
échantillonnage naturel, est la plus simple des MLI(s), tant du point de
vue de son principe, que de son implantation (analogique ou numérique).
[35].Pour déterminer les instants de commutation, elle consiste à
comparer entre elles :
· Une onde de référence sinusoïdale,
la modulatrice, de fréquence ???? = ?? (fréquence de
référence)
· Une onde dite porteuse, en général
triangulaire, de haute fréquence ????, respectant
l'inégalité : ???? » ??
La commande MLI est caractérisée par les
paramètres suivants :
L'indice de modulation « m »
????
??= ????????
|
(III.44)
|
|
Avec :
???? : fréquence de modulation ???????? :
fréquence de référence
64
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
Le taux de modulation « r » est
exprimé par :
Avec :
Vref : l'amplitude de la tension de
référence. V, :la crête de l'onde de
modulation.
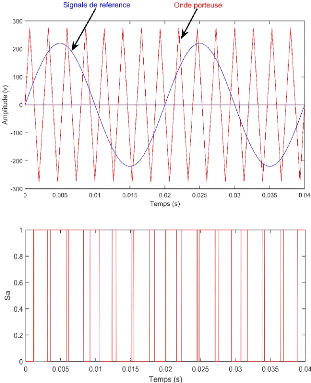
Figure III-13. Principe de fonctionnement de la technique MLI
triangulo sinusoïdal
III.6 Conclusion
Ce chapitre a permis d'écrire la modélisation
de la chaine de conversion de l'éolienne (turbine et MADA) tel que : la
turbine, le multiplicateur, l'arbre mécanique et la machine asynchrone
à double alimentation (MADA). D'autre part, l'éolienne
nécessite une stratégie de
65
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
commande afin de mieux gérer et contrôlé
l'énergie produite pour cela nous allons aborder la stratégie de
commande d'une éolienne dans le chapitre suivant.
66
| 


