Chapitre III : Modélisation de
la MADA et des convertisseurs
Statiques.
45
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
III.1 Introduction
Afin de compléter la chaine de conversion et de produire
de l'énergie électrique un générateur est
essentiels pour convertir l'énergie mécanique produite par
l'éolienne en énergie électrique et injectée aux
réseaux.
Il existe plusieurs types de générateurs dans
l'industrie, la génératrice électrique la plus
utilisée dans les systèmes éoliens à vitesse
variable de forte puissance est la génératrice électrique
de type machine asynchrone à rotor bobiné, qui est couramment
appelé Machine Asynchrone à Double Alimentation (MADA), car cette
dernière a l'avantage d'être facialement contrôlée et
présente des performances intéressantes.
Nous allons nous intéresser en premiers temps à
la modélisation de la machine asynchrone a double alimentation. Ensuite
afin d'injectée l'énergie électrique produite par le
générateur la nécessiter des convertisseurs de
l'électronique de puissance son primordial pour cela la
modélisation de ces dernier son présenté dans la
dernière partie de ce chapitre ainsi qu'une conclusion.
III.2 Description de la MADA
La machine asynchrone à double alimentation MADA, est
un générateur à rotor bobiné. La figure III.1
représente la structure d'une MADA connectée au réseau
triphasé. Les enroulements du stator sont reliés au réseau
à travers deux convertisseurs de puissance bidirectionnels en courant.
La puissance traversant ces convertisseurs peut alors être
absorbée ou produite par la machine selon le mode de fonctionnement, le
bus continu représenté ici : le condensateur entre ces deux
convertisseurs et un transformateur élévateur de tension qui
permet le raccordement au réseau de distribution [29].
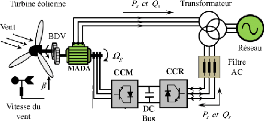
Figure III-1.Structure d'une MADA connectée au
réseau [30]
46
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
III.3 Mode de fonctionnement de la MADA
La machine asynchrone à double alimentation (MADA)
peut fonctionnée en 4 mode possible selon la vitesse de synchronisme.
III.3.1 Fonctionnement en moteur
hypo-synchrone
Le fonctionnement en mode moteur hypo synchrone de la MADA
est représenté par la figure III.2. On remarque que la puissance
est fournie par le réseau au stator et la puissance de glissement passe
par le rotor pour être réinjectée au réseau. On a
donc un fonctionnement moteur en dessous de la vitesse de synchronisme. La
machine asynchrone à cage classique peut fonctionner ainsi mais la
puissance de glissement est alors dissipée en pertes Joule dans le rotor
[31].
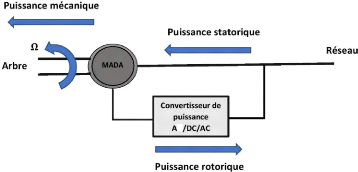
Figure III-2- Schéma de structure de la MADA en mode
moteur hypo-synchrone. [31]
III.3.2 Fonctionnement en moteur
hyper-synchrone
Le glissement devient négatif lorsqu'on augmente la
vitesse, la puissance est fournie par le réseau au stator et au rotor.
Pour réaliser ce mode on inverse l'ordre de phase de sorte que le champ
tournant induit par la fréquence du glissement soit en opposition de
phase avec celui du stator [29].
La figure III.3 représente le Schéma de structure
de la MADA en mode moteur hyper synchrone
47
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
Figure III-3.Schéma de structure de la MADA en mode
moteur hyper-synchrone [31]
III.3.3 Fonctionnement en mode génératrice
hyper-synchrone
Le fonctionnement en mode moteur hypo synchrone de la MADA
est représenté par la figure III.4. On s'aperçoit que la
puissance est transférée au réseau à travers le
stator et la puissance de glissement est récupérée
à travers le rotor pour être réinjectée au
réseau. On a donc un fonctionnement générateur au-dessus
de la vitesse de synchronisme. [31]
La machine asynchrone à cage classique peut avoir ce
mode de fonctionnement mais dans ce cas la puissance de glissement est
dissipée en pertes Joule dans le rotor [31]
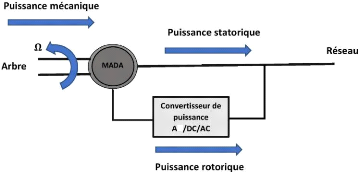
Figure III-4.Fonctionnement Génératrice
hyper-synchrone [31]
III.3.4 Fonctionnement en mode génératrice
hypo-synchrone
D'après la figure III.5 on remarque que le réseau
reçoit la puissance à travers le rotor, la
génératrice fonctionne donc en dessous de la vitesse de
synchronisme.
48
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
La figure III.5 montre que la puissance est fournie au
réseau par le stator. La machine asynchrone à cage classique ne
peut pas avoir ce mode de fonctionnement. [31]
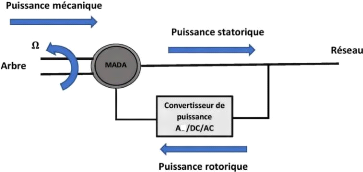
Figure III-5. Fonctionnement en mode génératrice
hypo-synchrone [31]
III.4 Modélisation de la MADA
Après avoir modélisé la partie
mécanique de l'aérogénérateur, nous allons
modéliser la machine asynchrone à double alimentation
l'élément phare de notre chaine de conversion pilotée par
le rotor liée à un convertisseur statique. Le modèle de la
MADA généralisé triphasé et biphasé de sera
présenté à travers cette section.
III.4.1 Modèle de la MADA dans le repère
triphasé-triphasé
La figure III.6 représente La représentation
électrique d'une machine triphasée asynchrone à double
alimentation dans le repère triphasé. Les trois enroulements
(bobinages) du stator sont représentés schématiquement sur
leurs axes magnétiques respectifs Sa, Sb et Sc qui
sont décalés
de 120°, ainsi que les trois enroulements du rotor sur
leurs axes magnétiques respectifs
Ra, Rb et
R?? [22].
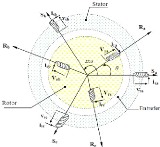
Figure III-6. Représentation spatiale des enroulements de
la MADA [22]
49
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
Avec :
(Vsa, Vsb, Vsc), (Vra, Vrb, Vrc) :
Les tensions simple aux bornes des enroulement statoriques et rotoriques.
(Isa, Isb, Isc), (Ira, Irb, Irc) : Les
courants de phase instantanés statorique et rotorique.
8 : L'angle électrique entre le
repère statorique Sa et le repère rotorique
Ra.
III.4.1.1 Hypothèse simplificatrice
La modélisation de la MADA, est établie sous les
hypothèses simplificatrices suivantes :
· L'entrefer est d'épaisseur uniforme et l'effet
d'encochage est négligeable.
· La saturation du circuit magnétique,
l'hystérésis et les courants de Foucault sont
négligeables.
· Les résistances des enroulements ne varient pas
avec la température et on néglige l'effet de peau.
· On admet que la f.e.m. créée par chacune
des phases des deux armatures est à répartition sinusoïdale.
[22]
III.4.1.2 Equation électrique
En générales les équations de la machine
asynchrone à rotor bobiné dans un repère triphasé
s'écrivent :
· Au niveau du stator
d
Vsa = RsIsa + dt (Psa
d
Vsb = RsIsb + dt (Psb
d
Vsc = RsIsc + dt (Psc
|
(III.1)
|
|
· Au niveau du rotor :
|
d
Vra = RrIra + dt (Pra
d
Vrb = RrIrb + dt (Prb
d
Vsc = RrIrc + dt (Prc
|
(III.2)
|
50
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
Ø En format matriciel :
· Au niveau du stator
??????
( ?????? )
??????
|
=
|
????
( 0
0
|
0
????
0
|
0 ??????
0 ) ( ??????
???? ?????? )
|
??
+
|
??????
( ??????
??????
|
)
|
(III.3)
|
|
|
· Au niveau du rotor :
??????
??????
??????
|
=
|
????
0
0
|
0
????
0
|
0
0
????
|
??????
??????)
??????
|
?? ??????
|
(III.4)
|
|
|
Avec :
(??????, ?????? , ??????), (??????, ??????, ??????) : Les
flux statoriques et rotoriques.
????, ???? : les résistance statorique et
rotorique.
III.4.1.3 Equation Magnétique
Les expressions des flux en fonction des courants statoriques
et rotoriques sont données par
[32] :
??????
( ??????
??????
??????
( ??????
??????
|
)=
) =
|
????
( ????
????
????
( ????
????
|
????
????
????
????
????
????
|
????
???? ) ????
????
???? ) ????
|
??????
(?????? )
??????
??????
(?????? )
??????
|
+ (??????)
+ (??????)
|
??????
( ?????? )
??????
??????
( ?????? )
??????
|
(III.5)
(III.6)
|
|
Avec :
???? , ???? : Inductances propres statoriques et rotoriques ????
: Inductance mutuelle entre phases statoriques ???? : Inductance mutuelle entre
phases rotoriques
La matrice des inductances mutuelles entre les phases du stator
et du rotor dépend de la position angulaire è entre l'axe du
stator et celui du rotor [33]
51
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
(??????)
|
=
|
????
|
??????
??????
|
????????
(?? - (??
|
2??
|
)
)
|
??????
??????
|
(??
???????? (??
|
4??
|
)
)
|
??????
??????
|
(??
(??
????????
|
2??
|
)
)
|
(III.7)
|
|
|
|
|
|
|
|
???? : Maximum de l'inductance mutuelle entre une phase du
stator et la phase correspondante du rotor.
III.4.1.4 Equation mécanique
L'équation de la dynamique appliquée sur la
machine est donnée par :
??Ù (III.8)
??. = ??????- ????- (????. Ù??)
????
Avec :
??
Ù =
??
?????? = ??[????]([??????][????])
Avec :
?? : Le moment d'inertie du rotor en [????. ??2].
Ù : La vitesse angulaire mécanique en
[??????/??].
??????: Le couple électromagnétique en [??.
??].
????: Le couple résistant en [??. ??].
????: Le coefficient de frottement en [??. ??. ??/??????].
?? : La vitesse angulaire électrique de rotation du rotor
en [??????/??].
p : Le nombre de pair de pole.
III.4.2 Modèle de la MADA dans le repère
de Park
III.4.2.1 Définition de la transformation de
Park
|
(III.9) (III.10)
|
|
La transformation de Park est composé d'une
transformation triphasé - diphasé suivie d'une rotation. Elle
nous permet de transformer un système dans un repère abc vers un
repère ???? en
52
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
passant par le repère ???? . Le repère ???? est
toujours fixe par rapport au repère ?????? comme le montre la figure
III.7, par contre le repère ???? est mobile. Il forme avec le
repère fixe ???? un angle qui est appelé l'angle de la
transformation de Park ou angle de Park. [34]
Le choix des angles de transformation de Park pour les grandeurs
statoriques et celle des grandeurs rotoriques doivent coïncider pour
simplifier ces équations. Ceci se fait en liant les angles ???? et ????)
par la relation [34] : ?? ?? = ???? + ??
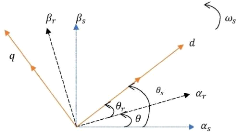
Figure III-7. Transformation de Park
On désire transformer les enroulements de la MADA
triphasée en des enroulements biphasés orthogonaux
équivalents selon les axes (????) lié au champ tournant ainsi la
composante homopolaire pour équilibrer le système
transformé, c'est à dire [32] :
· Direct selon l'axe (??).
· Quadrature (transversal) selon l'axe (??).
· Homopolaire (??).
Le produit matriciel définissant la transformation de PARK
s'exprime par :
[????????] = ??(??)[????????] (III.11)
Avec
:
|
????
|
|
????
|
|
[????????]
|
= [ ???? ] Et [????????]
|
=
|
[ ???? ]
|
|
????
|
|
????
|
??, ??, ?? : sont respectivement indice des composantes direct,
quadratique et homopolaire.
?? : représente l'angle de transformation, elle
dépend du choix du référentiel ainsi que des grandeurs
statoriques et rotoriques. La matrice de changement Park est exprimée
par l'équation II.12 :
53
Chapitre III : Modélisation de la MADA et des
convertisseurs statiques
[??(??)] = v3
2
[
|
2??
??????(??) ?????? (?? - 3 )
|
?????? (?? -34?? )
|
(III.12)
2??
4??
- ??????(??) - ?????? (?? - 3 ) - ?????? (?? - 3 )
1 1 1
v2 v2 v2
La transformation inverse de Park est donnée par :
[????????] = [??(??)]-1[????????] (III.13)
Avec :
|
[??(??)]-1 = v23
|
??????(??)
?????? (?? -
?????? (??+
|
|
- ??????(??)
|
1
|
(III.14)
|
|
v2
|
|
32??)- ??????
|
(?? - 32??)
|
1
v2
|
|
32??) -??????
|
(??+32??)
|
1
v2
|
Pour un système équilibré la composante
homopolaire est négligée, et en appliquant la transformation de
Park aux équations de la machine asynchrone dans le repère
naturel, on obtient les équations suivantes :
| 


