Chapitre II : Modélisation et
commande de l'éolienne
25
Chapitre II : Modélisation et commande de
l'éolienne
II.1 Introduction
Afin de bénéficier et de mieux profité
des avantages de l'énergie éolienne en termes d'énergie
propre et inépuisable, l'énergie cinétique du vent doit
être convertie en énergie électrique et pour cela toute une
chaine de conversion est mise à disposition.
Cette chaine de conversion est composée de plusieurs
éléments importants comme la turbine éolienne, le
générateurs et les convertisseurs de l'électronique de
puissance.
Pour que cette chaine de conversion soit parfaitement
fonctionnelle et contrôlée, la modélisation des
éléments constituants cette dernière est primordiale. Dans
le cadre de nos travaux, nous avons choisi d'étudier une éolienne
à vitesse variable.
Ainsi, dans ce deuxième chapitre nous allons en
premier temps, nous intéresser à la modélisation de la
partie mécanique de la chaine de conversion de l'éolienne qui est
la turbine et ses composant, ensuite nous allons présenter la
stratégie de commande de l'éolienne. A la fin de ce chapitre, les
résultats de simulation et une conclusion seront
présentés.
II.2 Modélisation du vent
Le vent est l'élément essentiel pour faire
fonctionner une éolienne, c'est pour cela qu'il est primordial de
connaitre son modèle mathématique. La vitesse du vent est une
fonction scalaire qui évolue dans le temps V = ??(??) La
définition du modèle nécessite des données
géographiques et climatiques du site concerné, ainsi que la
période de la saison concernée par l'étude.
Généralement le modèle du vent est exprimé par une
équation en série de Fourier qui le présente comme un
signal constitué par une superposition de plusieurs harmoniques, il est
donné par l'équation suivante :
[20].
??
V??(??) = A + ? ??????i??(??????)
??=1
Avec :
A : la valeur moyenne de la vitesse du vent. ????
: amplitude de l'harmonique de l'ordre k. ???? : pulsation de
l'harmonique de l'ordre k.
i : le rang du dernier harmonique retenu dans le calcul
du profil du vent.
26
|
(II.1)
|
|
Chapitre II : Modélisation et commande de
l'éolienne
II.3 Modélisation de la turbine
La figure II.1 représente le schéma global d'une
turbine éolienne.
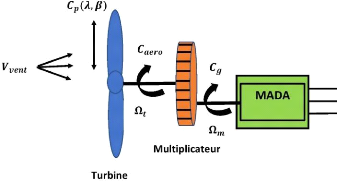
Figure II-1. Structure d'une turbine éolienne.
Similaire aux ailes d'avions, la forme aérodynamique
des pales modifie la vitesse du vent sur l'extrados et l'intrados des pales. La
différence de vitesse produit une différence de pression, donc
une force portante est générée.
La puissance du vent est donnée par l'équation
II.2
????=
|
1
2 ?? S ??????????
3
|
(II.2)
|
|
Avec :
??: est la densité de l'air en ????/??3 (au
niveau de la mer et à 20C° :?? = 1.225????/??3). ????:
Est le coefficient de puissance de la turbine.
S : la surface circulaire balayée par la turbine.
?????????? :la vitesse du vent.
La puissance aérodynamique captée par une turbine
est donnée par :
27
Chapitre II : Modélisation et commande de
l'éolienne
?????????? =
|
1
2 ?? ???? S ??????????
3
|
(II.3)
|
|
Avec :
????: Le coefficient de puissance de la turbine.
????(??, ??) 1
|
116
=
|
0.4
|
??
|
-
|
5)??
|
-21
|
(II.4)
(II.5)
|
|
|
|
0.08?? ??3 + 1
|
|
Avec :
?? : Angle d'inclinaison des pales. ?? : Ratio de la vitesse.
La figure II.2 représente la variation du
paramètre ???? en fonction du ratio de vitesse ?? et de l'angle de
l'orientation de pale ??.
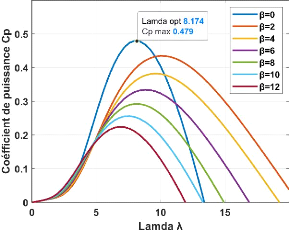
Figure II.2-Coefficient de puissance et vitesse relative pour
différents angles de calages.
D'après la figure II.2 obtenu on remarque que quand
l'angle d'orientation de pale ?? augmente, le coefficient de puissance ?? ??
diminue, la valeur maximale de ?? ?? d'après la figure
28
Chapitre II : Modélisation et commande de
l'éolienne
obtenue est de ????_?????? = 0.48 ,cette valeur correspond
à un angle d'orientation de pale égale à ?? = 0 et une
valeur optimale de la vitesse ???????????? = 8.1 .
Afin de maintenir ë à sa valeur nominale ou
optimale, et donc maximiser la puissance de la turbine éolienne, il est
donc impérativement important de varier la vitesse de rotation ???? de
manière linéaire avec la vitesse du vent. L'équation (I.3)
deviens alors :
???????? =
|
?? .??????????
??????????
|
(II.6)
|
|
Avec :
R : rayon des pales.
Le couple aérodynamique est exprimé en fonction
de la puissance aérodynamique et la vitesse de rotation de la turbine
comme le montre l'équation I.7:
????????
???????? = ????????
|
1 (II.7)
2 ?????? ?? ??2 ??????????
3 1
????????
|
|
II.4 Modélisation du multiplicateur
Le multiplicateur est représentée sur la figure
II-3 est l'élément qui se situe entre la turbine et le
générateur. Sa fonctionnalité est le réglage de la
vitesse de la turbine ???? qui est lente à la même vitesse de la
génératrice ???? .
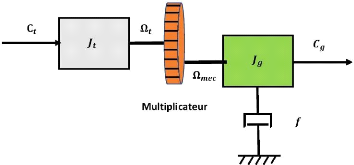
Figure II-3. Modèle d'un multiplicateur [21]
29
Chapitre II : Modélisation et commande de
l'éolienne
Le multiplicateur est représentée sur la figure
II-3 est l'élément qui se situe entre la turbine et le
générateur. Sa fonctionnalité est le réglage de la
vitesse de la turbine ???? qui est lente à la même vitesse de la
génératrice ???? .
En négligeant les pertes mécaniques sont
négligeables, le multiplicateur peut être modélisé
mathématiquement par l'équation suivante :
???????? = ??. ????
Avec :
?? : gain du multiplicateur.
|
(II.8)
|
|
II.5 Modélisation de l'arbre
mécanique
L'arbre mécanique est composé d'une masse
correspondant à l'inertie du rotor de la
turbine la figure II.5
représente modèle de transmission mécanique ramenée
à l'arbre mécanique.
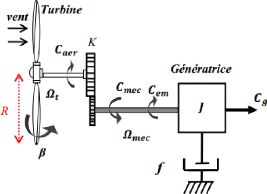
Figure II-4. Modèle de transmission mécanique
ramenée à l'arbre Mécanique [22]
Dans le modèle mécanique proposé dans la
figure II .4, l'inertie totale ?? est celle du générateur ???? et
l'inertie de la turbine ???? ramenée sur l'arbre rapide (au rotor du
générateur) où : [22]
??= ????+ ???? ??2 (II.9)
Le couple mécanique appliqué au rotor de la
génératrice est exprimée par :
30
|
Chapitre II : Modélisation et commande de
l'éolienne
|
|
????????
????????
???? -
|
???? ??????
|
????????
+ ??????????
|
(II.10)
(II.11) (II.12)
|
|
|
|
Avec :
???????? : La vitesse mécanique.
???????? : Le couple mécanique appliqué au
rotor de la génératrice.
???????? : Le couple de frottement visqueux.
???? : Le couple du multiplicateur de vitesse.
?? : Coefficient de frottement visqueux.
?? : Inertie totale.
La figure II.5 représente Le schéma bloc
correspondant à la modélisation de la turbine
modélisée.
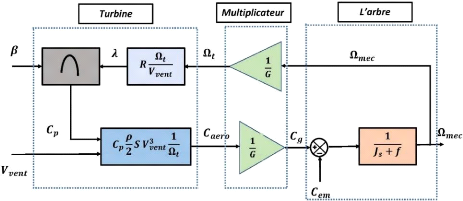
Figure II-5. Schéma bloc de la turbine
modélisée. [2]
II.6 Stratégie de commande de
l'éolienne
Le contrôle de l'éolienne se fait à
travers deux boucles de régulation ; boucle de régulation de la
vitesse et la boucle de régulation de la puissance.
31
Chapitre II : Modélisation et commande de
l'éolienne
A travers la boucle de régulation de la vitesse la
vitesse de rotation est contrôlée par le couple
électromagnétique, cette boucle de régulations est la
boucle principale dans la stratégie de d'optimisation de puissance. La
vitesse de rotation est ajustée dans cette boucle afin d'extraire le
maximum de la puissance du vent quand la vitesse du vent va dépasser la
vitesse nominale et l'angle de calage vas être maintenue constant a une
valeur optimale ????????.
La boucle de régulation de vitesse réagit
instantanément en adaptant la puissance de référence de la
génératrice en agissant sur le dispositif d'orientation des pales
afin de contrôlée le couple électromagnétique et la
vitesse de rotation. Cette action est enclenché que quand la vitesse de
rotation va augmenter rapidement suite à des rafales de vent et peut
dépasser la vitesse de rotation des pales.
II.6.1 Systèmes de régulation de la
vitesse de rotation de l'éolienne
II.6.1.1 Système à décrochage
aérodynamique "Stall"
Ce système de régulation est
représenté par la figure II-6, il est simple et relativement
fiable mais il manque de précision car il dépend de la masse
volumique de l'air et de la rugosité des pales donc de leur état
de propreté. Il peut dans certains cas, être
amélioré en autorisant une légère rotation de la
pale sur elle-même (système "Stall actif") permettant ainsi de
maximiser l'énergie captée pour les faibles vitesses de vent.
Pour les fortes vitesses de vent, la pale est inclinée de façon
à diminuer l'angle de calage â et renforcer ainsi l'effet "stall"
de la pale. La répercussion des variations de vitesse de vent sur le
couple mécanique fournie par l'éolienne est ainsi moins
importante [23].
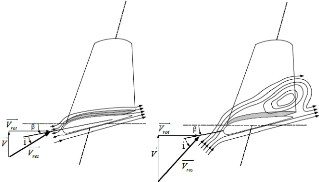
Figure II-6. Flux d'air sur un profil de pale " Stall "
[23]
32
Chapitre II : Modélisation et commande de
l'éolienne
II.6.1.2 Système d'orientation des pales
"Pitch"
Le système d'orientation des pales agit sur la portance
des pales pour garder la puissance autour de sa valeur nominale [24]. En
réglant l'angle de calage, on agit sur les performances de
l'éolienne et plus précisément sur le coefficient de
puissance.
Le système d'orientation des pales génère
alors un angle de calage de référence : ????????. La dynamique de
l'actionneur pitch est généralement décrite par la
fonction de transfert de premier ordre suivante [25].
1
?? = 1 + ?????? ????????
Avec :
|
(II.13)
|
|
ô??: Constante du temps du système actionneur
pitch. ?? : Angle de calage des pales.
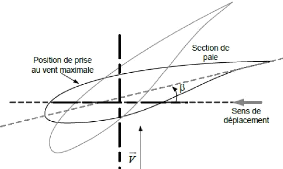
Figure II-7. Variation de l'angle de calage d'une pale
[23]
Lors de la modélisation du système
d'orientation des pales, il est essentiel de modéliser la vitesse de
variation de cet angle [24]. En effet, compte tenu des efforts subis par les
pales, la variation de l'angle de calage doit être limitée
à 10%. La valeur de saturation de l'angle de calage en position est de
90°, cette valeur correspond à la mise en drapeau des pales
[24].
L'agitation sur l'angle de calage des pales entraine la
modification des performances du système, et plus
précisément sur le coefficient de puissance ????, les pales sont
face au vent pour les basses vitesses (?? = 0°), pour des vitesses plus
importantes du vent les pales s'inclinent afin de dégrader le
coefficient de puissance ???? [2].
33
Chapitre II : Modélisation et commande de
l'éolienne
II.7 Zone de fonctionnement de l'éolien
:
Les éoliennes fonctionnent dans une plage de vent
très variables. Une vitesse de vent spécifique est
nécessaire afin que les pales de l'éolienne puissant
surmonté l'inertie et la friction. On appel cette vitesse la vitesse du
vent de démarrage ???? ,la vitesse du vent est évaluée en
moyenne de 3 à 5 m/s afin d'éviter d'endommager les pales de
l'éolienne, il est recommandé d'utiliser une vitesse
d'entrée de 25 m/s [8].
Les différentes zones de fonctionnement d'une
éolienne sont illustrées à travers la figure II.8, on
distingue quatre zones de fonctionnement :
Zone I : :la puissance captée est
très faible à cause de la faible vitesse du vent.
Zone II : dans cette zone la vitesse du vent
est supérieure à la vitesse de seuil et inférieure
à la vitesse nominale de l'éolienne. Dans cette partie qui est
caractérisée par une puissance proportionnelle au cube de la
vitesse du vent, l'angle de calage est maintenu constant, et c'est le
contrôle du couple électromagnétique de la
génératrice qui va être mis en oeuvre (principe de MPPT).
Ceci se fait en gardant le coefficient de puissance ???? = ?????????? de
manière à tirer le maximum de profit de la vitesse du vent et
généré le maximum d'énergie électrique
possible. Dans cette zone, la courbe de puissance de la
génératrice suit une progression rapide [8].
Zone III : Dans cette zone la vitesse de
vent est supérieure à la vitesse nominale et inférieure
à la vitesse maximale de déclenchement, le coefficient de
puissance ?? ?? doit être contrôlé. L'augmentation de la
vitesse de vent va s'accompagner d'une diminution du coefficient ?? ?? et d'une
augmentation moins rapide de la puissance récupérée.
Lorsque la puissance maximum de la génératrice est atteinte,
l'angle des pales (pitch) est modifié afin de dégrader encore
plus le coefficient Cp. [8, 26]
Zone IV : la vitesse de vent devient trop
forte et dans laquelle le système de sûreté du
fonctionnement arrête la rotation et le transfert de l'énergie
afin d'éviter tout disfonctionnement ou dégât [8] .
34
Chapitre II : Modélisation et commande de
l'éolienne
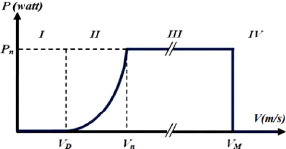
Figure II-8. Courbe de la puissance éolienne en fonction
de la vitesse du vent [8]
II.8 Principe de contrôle MPPT (Maximum Power
Point Tracking)
Le système de contrôle le plus répandu
des éoliennes traditionnelles directement connectées au
réseau électrique de distribution, est basé principalement
sur la technique d'extraction du maximum de puissance (MPPT) et ce sans
supervision centralisée. [18]
Le principe de la stratégie MPPT consiste à
contrôler la vitesse de rotation de la turbine éolienne en
fonction de la vitesse du vent, en fonction de la vitesse du vent de rotation
de la turbine éolienne est maintenue à une valeur de
référence pour maintenir une vitesse relative optimale et donc un
coefficient de puissance maximal Cpmax [18].
Lorsqu'un problème technique ou la présence
d'éventuel défaut sur la commande MPPT, un dispositif
déconnecte immédiatement l'éoliennes du réseau
electrique.la commande MPPT ne peut
en aucun cas intervenir au contrôle de la production de la puissance en
temps réel.On distingue deux types de commande :
· Le contrôle MPPT sans asservissement de la vitesse
mécanique.
· Le contrôle MPPT avec asservissement de la vitesse
mécanique.
II.8.1 Maximisation de la puissance sans asservissement
de vitesse :
Ce mode de contrôle repose sur l'hypothèse que
la vitesse du vent varie très peu en régime permanent devant les
constantes de temps électriques du système éolien [27], ce
qui implique que le couple d'accélération de la turbine peut
être considéré comme nul.
C
't l dflm (II.18)
G2 + 'm)
dt + Îvflm = Cm - Cem = 0 35
Chapitre II : Modélisation et commande de
l'éolienne
La figure II.9 représente le schéma bloc de la
maximisation de la puissance sans asservissement de la vitesse
mécanique.
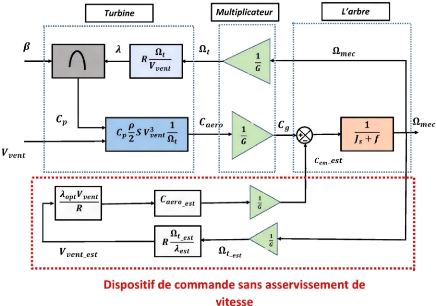
Figure II.9- Schéma bloc de la maximisation de la
puissance sans asservissement de la
vitesse mécanique. [28]
Une estimation de la vitesse de rotation de la turbine,
notée ???-??????, est obtenue à partir de la mesure de la vitesse
de rotation de la MADA et donné par l'équation II.19 :
???
???_?????? = ??
|
(II.19)
|
|
Le couple de la turbine éolienne peut ensuite
être obtenu à partir des estimations de la vitesse du vent et de
la vitesse de rotation de la turbine. Il peut s'exprimer par :
??. ?? 1 (II.20)
????_?????? = ????. 2 . ???_?????? - ?????????? _??????
3
Le couple électromagnétique de
référence est alors obtenu à partir de l'estimation du
couple de la turbine éolienne :
???* ??? =
|
????_??????
|
(II.21)
|
|
|
|
36
Chapitre II : Modélisation et commande de
l'éolienne
Afin d'extraire le maximum de puissance, il faut fixer la
vitesse relative à sa valeur optimale Aopt afin d'obtenir le
coefficient de puissance maximum Cpmax le couple
électromagnétique de référence s'exprime donc par
l'équation II.22 :
Ce*?m = K. SZm2?
(II.22)
Où K est une constante définie par :
II.8.2 Maximisation de la puissance avec asservissement
de la vitesse
Le vent est une grandeur stochastique, de nature très
fluctuante. Cette fluctuation engendre des perturbations dans le système
de conversion éolien, et crée des variations continues de
puissance. De cet effet, il est supposé que le couple
électromagnétique développé par la machine soit
égal à sa valeur de référence quel que soit la
puissance générée [20].
Le couple électromagnétique Cem
produit par la MADA est donc à tout instant égal à sa
valeur de référence Cem * imposée par la
stratégie de commande [21].
Cem = Cem-ref (II.14)
Cem-rref = Cass (
·aref -
·amec)
(II.15)
Avec :
Cass : régulateur de vitesse
S1re f : vitesse mécanique de
référence
La vitesse mécanique de référence
dépend de la vitesse de la turbine afin de maximiser la puissance
extraite. La vitesse mécanique de référence est
exprimée par l'équation suivante :
· aref = G.
·atur-ref
(II.16)
Avec :
G : gain du multiplicateur.
37
Chapitre II : Modélisation et commande de
l'éolienne
La référence de la vitesse de la turbine
correspond à la valeur optimale du ratio de vitesse Aopt
permettant d'obtenir la valeur maximale du coefficient de puissance
Cp. On peut déduire [20]:
ftur-ref =
|
ACpmax. event
R
|
(II.17)
|
|
La figure II.10 représente le schéma bloc de la
maximisation de la puissance avec asservissement de la vitesse
mécanique.
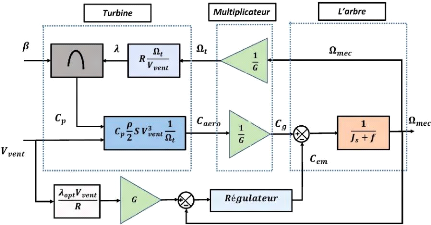
Figure II-10. Schéma bloc de la maximisation de la
puissance avec asservissement de la vitesse mécanique [28]
· Synthèse du régulateur
PI
Un correcteur PI a été choisie afin de
réguler notre système, ce correcteur a pour fonction de transfert
: kpu, + kP .
On peut exprimer la fonction de transfert qui lie la vitesse
aux couples électromagnétique et au couple mécanique
à partir de l'équation de la mécanique régissant la
dynamique des corps en rotation par :
38
Chapitre II : Modélisation et commande de
l'éolienne
La figure II.11 représente le schéma bloc de la
régulation de vitesse :
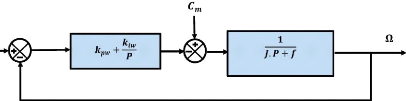
Figure-II.11- Schéma bloc de la régulation de
vitesse avec régulateur PI.
On peut exprimer la fonction de transfert du système en
boucle ouverte par l'équation suivante :
?????? =
|
Ù
= Ù*
|
??????. ?? + ??????
??.??2 + ??. ??
|
(II.19)
|
|
La fonction de transfert de la vitesse en boucle fermée
est donnée par :
?????? =
|
??????. ?? + ??????
??
|
(II.20)
|
|
|
|
Cette fonction de transfert est de la dynamique du
deuxième ordre, sa forme canonique est donnée
par :
??(??) = ??2 + 2??. ?????? + ????2
2. ??. ?????? + ???? 2 (II.21)
Avec :
?? : le coefficient d'amortissement.
???? : la pulsation propre.
Après identification de l'équation II.20 avec
l'équation II.21 on obtiens :
2 ?? ????=
|
?????? + ??
??
|
(II.22)
|
|
??????
??
???? 2 =
D'après l'équation II.22 les paramètres du
régulateur PI auront pour expression :
39
Chapitre II : Modélisation et commande de
l'éolienne
{
?????? = 2 ?? ???? ?? - f (II.23)
?????? =
?? ???? 2
II.9 Résultat de simulation
La figure II.12 représente le profil du vent
appliqué à travers notre étude. Ce dernier est
caractérisé par l'équation suivante :
?????????? = 8.5 + 0.2 sin(0.1047t) + 2 sin(0.2665t) +
sin(1.2930t) + 0.2sin (3.6645t)
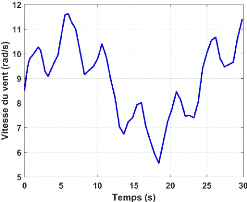
Figure II.12- Profil du vent appliqué.
Dans cette section de chapitre la simulation de la partie
mécanique de la chaine de production ;
l'aérogénérateur avec s'est différente commande
MPPT avec et sans asservissement de la vitesse mécanique qui on
était citée dans les paragraphes précèdent vont
être simuler afin d'analyser la meilleure commande MPPT possible, les
simulations on était réalisé sans raccordée
l'éolienne à la génératrice.
Les deux simulations on était effectuée sous le
logiciel MATLAB/Simulink en considérant les paramètres suivants
:
Tableau II-13. Paramètre nominal de la simulation de la
partie mécanique.
Angle de calage ??
|
0
|
Ratio de vitesse A??????
|
8.1
|
Coefficient de puissance
maximal ????_??????.
|
0.48
|
Vitesse moyenne du vent
|
8.5m/s
|
|
40
Chapitre II : Modélisation et commande de
l'éolienne
Les paramètres de la turbine éolienne
utilisée dans ce travail et sa structure implémenté sous
MATLAB/Simulink sont représenté dans l'annexe A et l'annexe B
respectivement.
II.9.1 Résultats de simulation de la turbine avec
asservissement de la vitesse mécanique
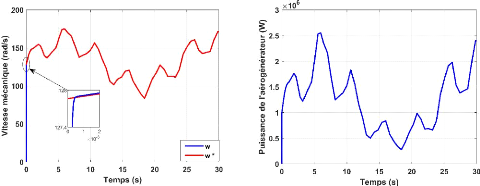
Figure II.13. (a)-Vitesse de rotation mécanique. Figure
II.13. (b)-Puissance de l'aérogénérateur
produite.
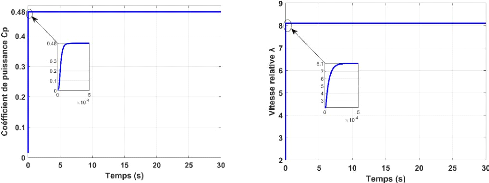
Figure II.13. (c)-Coefficient de puissance C??. Figure
II.13. (d)-Vitesse relative A.
41
Chapitre II : Modélisation et commande de
l'éolienne
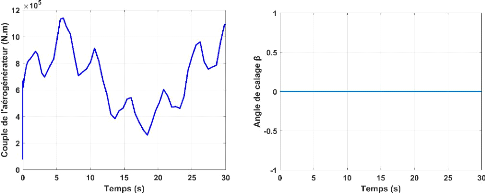
Figure II.13. (e)-Couple électromagnétique de
Figure II.13. (f)-Angle de calage ??.
l'aérogénérateur.
Figure II.13-Resultat de simulation de la commande MPPT avec un
asservissement de la vitesse
mécanique.
· Interprétation des
résultats
Les résultats de la simulation de la méthode de
contrôle MPPT avec un asservissement de vitesse mécanique à
l'aide d'un régulateur PI son représenté par la figure II
.13.
Les figure II.13.b. et II.13.e. illustre respectivement la
puissance de l'aérogénérateur et le couple de
l'aérogénérateur. D'après la figure II.12. On
constate une nette influence de la variation de la vitesse du vent sur le
couple et la puissance généré par
l'aérogénérateur. Cette influence varie
proportionnellement à la vitesse de variation du vent
Le coefficient de puissance C ?? et la vitesse relative
évolue jusqu'à ce qu'il atteigne leurs valeurs maximales de C ??
= 0.48 et ???????? = 8.1 sans dépassement pour un angle de calage
â=0° comme le montre les figures II.13c et II13d respectivement.
La vitesse de rotation mécanique (figure.II.13.a)
varie au cube de la vitesse de variation du vent et suit parfaitement sa
consigne imposée ceci est dû au contrôle du
régulateur PI.
II.9.2 Résultats de simulation de la turbine
sans asservissement de la vitesse mécanique
42
Chapitre II : Modélisation et commande de
l'éolienne
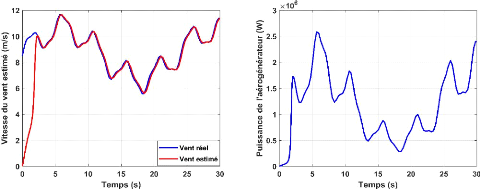
Figure II.14. (a)-Vitesse du vent estimée et Figure
II.14. (b)-Puissance de l'aérogénérateur
mesuré. produite.
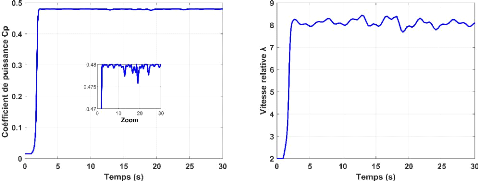
Figure II.14. (c)-Coefficient de puissance C??. Figure
II.14. (d)-Vitesse relative A.
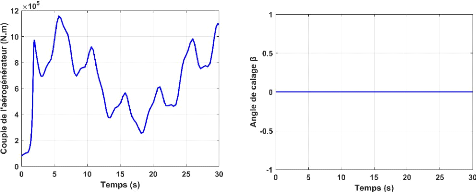
Figure II.14. (e)-Couple électromagnétique Figure
II.14. (f)-Angle de calage ??.
43
Chapitre II : Modélisation et commande de
l'éolienne
Figure II.14-Resultat de simulation de la commande MPPT sans
un asservissement de la vitesse
mécanique.
· Interprétation des
résultats
Les résultats de la simulation de la méthode de
contrôle MPPT sans un asservissement de vitesse mécanique sont
représenté sur la figure II .14.
La puissance et le couple aérodynamique
illustré respectivement dans Les figure II.14.b. et II.13.e, varient
proportionnellement avec la variation du profil du vent (figure II.12). Le
coefficient de puissance C ?? et la vitesse relative évolue
jusqu'à ce qu'il atteigne leurs valeurs maximales de C?? = 0.48 et
???????? = 8.1 pour un angle de calage ?? = 0° avec un temps de
réponse au démarrage comme le montre les figures II.13.c, II.13.d
et II.13.f..
La vitesse du vent mesuré suit la vitesse du vent
estimé avec une erreur statique importante en régime permanant
comme la montre la Figure II.14.a, ceci est dû à l'absence du
contrôle du régulateur PI.
II.10 Conclusion
Dans ce chapitre, nous avons tout d'abord
procédé à la modélisation de la turbine
éolienne a vitesse variable basée sur une machine asynchrone a
double alimentation (MADA), de la modélisation du vent jusqu'au
multiplicateur.
En premier temps, nous avons présenté dans ce
chapitre les différents modes de régulation de vitesse de
rotations de l'éolienne, les zone de fonctionnement d'une turbine
éoliennes a vitesse variable ont également été
présentée dans cette partie de chapitre.
En deuxième temps nous avons présentée
l'algorithme de maximisation de puissance MPPT , utilisé dans le
système éolien étudié, à l'aide d'un
asservissement de vitesse contrôlé par un régulateur de
type PI (proportionnel intégral), dont les paramètres sont
calculés par la méthode analytique.
En fin, la simulation et la présentation des
résultats obtenue d'un asservissement avec contrôle de la vitesse
on était présentée.
Le chapitre suivant est consacré à la
présentation et la modélisation de la partie électrique de
la chaine de conversion d'une éolienne qui est basée sur une
machine asynchrone à double alimentation, les convertisseurs statiques
seront également présentés et modélisé.
44
| 


