III.1.4.3. Analyse de la coïntégration.
L'analyse de la cointégration, présentée
par GRANGER (1983), puis par ENGLE et GRANGER (1987), est
considérée comme un des concepts les plus importants dans
l'analyse des séries temporelles.Le concept de cointégration
traduit l'idée selon laquelle des variables non stationnaires
individuellement peuvent évoluer de concert, suivre une évolution
parallèle dans le long terme et que leur relation dégage donc un
résidu stationnaire, de moyenne et de variance bien définies.
Ainsi, deux séries non stationnaires seront dites
cointégrées et liées par une réelle relation de
long terme si et seulement si leurs trajectoires sont convergents,
c'est-à-dire si elles évoluent dans des directions à peu
près, ou tout à fait parallèles. Par exemple, deux
séries, xt et yt sont dites
cointégrées si les suivantes conditions sont
vérifiées :
- Elles ont une tendance stochastique de même ordre
d'intégration d ;
- La combinaison linéaire de ces séries permet
à celles-ci de se ramener à une série d'ordre
d'intégration inférieur.
Soit: Xt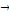 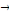 I (d) et Yt I (d) et Yt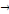 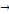 I (d); d étant le degré d'intégration tel que I (d); d étant le degré d'intégration tel que 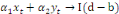 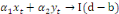 , avec d = b > 0. , avec d = b > 0.
On note :Xt, Yt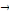  C I (d, b) où C I (d, b) où 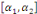 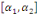 est le vecteur de cointégration. est le vecteur de cointégration.
Si l'ordre d'intégration est vérifié, on
estime par les MCO la relation de long terme entre les variables. Pour le cas
de 2 variables, on a : 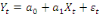 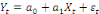 . La relation de cointégration est acceptée si le
résidu et issu de cette régression est stationnaire
à niveau, ( . La relation de cointégration est acceptée si le
résidu et issu de cette régression est stationnaire
à niveau, (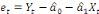 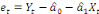 ). ).
La stationnarité du résidu est testée
à l'aide des tests DF ou DFA. Si le résidu est stationnaire
à niveau et que les variables sont intégrées de même
ordre, surtout I(1) et aussi coïntégrées, il est convenable
de procéder à une modélisation de type Modèle
à Correction d'Erreurs (MCE).
III.1.4.4. Le Modèle à correction d'Erreurs
ENGLE et GRANGER (1987) ont démontré que toutes
les séries cointégrées peuvent être
représentées par un MCE. De même, un théorème
important, connu sous le nom de théorème de représentation
de Granger, énonce que si deux variables Y et X sont
cointégrées, la relation entre ces variables peut s'exprimer
comme un MCE.
La cointégration ayant été
révélée, deux cas de figure sont envisageables :
- Soit, il existe un vecteur unique de
cointégration.
- Soit, plusieurs vecteurs de cointégration
existent.
Si le vecteur de cointégration est unique, l'estimation
du modèle à correction d'erreur se fait en deux étapes,
tel que cela est envisagée par ENGLE et GRANGER.
Etape 1 : Estimation par les MCO de la
relation de long terme et calcul du résidu.
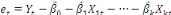 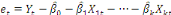 . .
Etape 2 : Estimation par les MCO de la
relation du modèle dynamique (court terme).
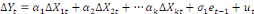 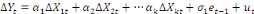 . .
Le coefficient 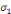 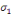 , appelé force de rappel vers l'équilibre, doit être
négatif et significatif. , appelé force de rappel vers l'équilibre, doit être
négatif et significatif.
Cependant, si le vecteur de coïntégration n'est
pas unique, la méthode d'Engle et Granger n'est plus valide. Par
conséquent, nous devons faire appel à une représentation
Vectorielle à Correction d'Erreur (VECM).
| 


