III.1.4. Présentation théorique de la
démarche économétrique
III.1.4.1. Détermination du nombre de retards
Nous pouvons postuler que, dans certaines
spécifications de modèles économétriques temporels,
la variable endogène dépend des valeurs prises par une variable
exogène à des époques antérieures, tel
que :
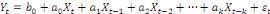 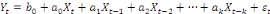 . .
Il est obligatoire de savoir où arrivent les
décalages. Ainsi, des différentes méthodes permettent de
déterminer le nombre de retards d'un modèle
économétrique temporel donné. Le nombre de retards retenu
est celui qui minimise la somme des carrés des résidus (SCR) et
maximise le coefficient de détermination.
Trois méthodes sont utilisées dans la
détermination du nombre de retard optimal :
- Le test de Fisher qui consiste à tester
l'hypothèse de nullité des coefficients de régression pour
les retards supérieurs à k, k étant le retard optimal.
- Le critère d'Akaike (AIC) qui consiste à
retenir comme valeur de k, celle qui minimise la fonction d'Akaike
donnée comme suit :
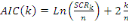 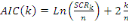 . .
Avec SCRk : Somme des Carrés des
Résidus pour le modèle à k retards.
n : nombre d'observations disponibles (chaque retard
entraine la perte d'une observation).
Ln : Logarithme népérien.
- Le critère de Schwarz (SC), proche du critère
d'Akaike, qui consiste à retenir la valeur de k qui minimise la fonction
de Schwarz libérée ainsi :
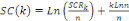 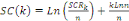 . .
III.1.4.2. Analyse de la stationnarité des
variables
Comme BOURBONNAIS (2003) le précise, les
théories économiques remettent en cause les résultats
obtenus par les études utilisant les régressions des
séries temporelles sans vérifier la stationnarité des
variables, l'existence de racine unitaire et leur coïntégration.
En effet, la plupart des variables économiques sont
générées par un processus non stationnaire. Les
théories économétriques consistent donc à
vérifier la stationnarité des séries temporelles et les
rendre stationnaires pour pouvoir les appliquer à des techniques
statistiques. La tendance d'affirmer ou d'infirmer de façon intuitive
certaines réalités en faisant seulement recours à la
théorie peut conduire à des conclusions quelque peu
erronées.
Le test de stationnarité largement répandu
depuis des années est celui de racine unitaire. Le point de
départ est le processus de racine unitaire défini comme
suit :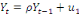 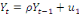 (-1 = ñ =1).Si ñ = 1, nous sommes en situation de non
stationnarité, dans ce cas, la variance de Yt n'est pas
stationnaire. Toutefois, si |ñ|< 1, la série chronologique
Yt est stationnaire dans le sens dont on la définit. (-1 = ñ =1).Si ñ = 1, nous sommes en situation de non
stationnarité, dans ce cas, la variance de Yt n'est pas
stationnaire. Toutefois, si |ñ|< 1, la série chronologique
Yt est stationnaire dans le sens dont on la définit.
Cependant, les différents tests de racine unitaire
utilisés sont :
- Le test de Dickey-Fuller (DF) qui permet la mise en
évidence du caractère stationnaire ou non d'une série
chronologique par la détermination d'une tendance déterministe ou
stochastique ;
- Le test de Dickey-Fuller augmenté (DFA) qui part
de l'hypothèse que le terme de l'erreur (ut) n'est pas
corrélé. Par contre, il n'y a aucune raison pour que, a priori,
l'erreur soit non corrélée. C'est ainsi que Dickey et Fuller ont
mis au point un test qui prend en compte l'hypothèse de l'existence de
la corrélation des erreurs. C'est le test Dickey-Fuller Augmenté
(DFA) ;
En considérant les trois équations du test DF,
le test DFA est effectué en ajoutant à celles-ci des valeurs
décalées de la variable dépendante. Le test DFA est
fondé sur l'estimation par les MCO des trois modèles sous
l'hypothèse alternative, H1 :
|Ö1|< 1.
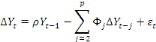
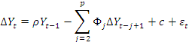
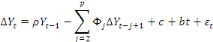
Ce test se déroule de la même manière que
le test DF, tout en se servant des tables statistiques différentes. La
valeur de p peut être déterminée selon les
critères d'Akaike et de Schwarz.
Ou encore, en partant d'une valeur suffisamment importante de
p, on estime un modèle à p-1 retards, puis
à p-2 retards, jusqu'à ce que le coefficient du
pième retard soit significatif.
- Le test de Phillips et Perron (PP) qui constitue le
prolongement des tests DF et DFA. Phillips et Perron utilisent des
méthodes statistiques non paramétriques pour prendre en compte la
corrélation sérielle dans les termes d'erreur sans pour autant
ajouter des termes de différence décalés.
La statistique PP donnée par :
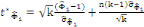 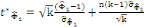 , Avec , Avec 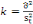 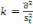 , est à comparer aux valeurs critiques de la table de MacKinnon.
Le logiciel EVIEWS facilite l'utilisation de ce test. En effet, cette
statistique ainsi que les valeurs critiques sont fournies automatiquement. , est à comparer aux valeurs critiques de la table de MacKinnon.
Le logiciel EVIEWS facilite l'utilisation de ce test. En effet, cette
statistique ainsi que les valeurs critiques sont fournies automatiquement.
Les critères de rejet ou d'acceptation de
l'hypothèse nulle sont les mêmes que pour ceux des tests DF et
ADF.
| 


