Effets de la fiscalité directe des entreprises et des ménages sur la consommation privée au burundi

III.1.4.5. Tests d'évaluation des résultats

a. Tests de significativité du modèle

Pour juger la significativité de notre modèle, quelques tests ont été empruntés.La significativité des variables de façon individuelle a été analysée sur base de la statistique t de Student tandis que la significativité des coefficients pris globalement a été illustrée par la valeur de la statistique F de Fisher.

Par ailleurs, au regard de la valeur du coefficient de détermination R² et surtout R²-ajusté, un modèle peut être jugé valide ou non.En effet, le coefficient de détermination permet d'indiquer le pourcentage de la variation totale de la variable dépendante due à la présence des variables explicatives.

La valeur de R² varie entre 0 et 1. Nous concluons que les variables indépendantes n'expliquent pas la variation de la variable dépendante si le coefficient de détermination tend vers 0. Par contre, si R² tend vers 1, ceci indique que la variable expliquée varie en fonction des variables explicatives.Quant au coefficient R²-ajusté, celui-ci est ajusté aux degrés de liberté et augmente avec le pouvoir explicatif du modèle. Il diminue avec les pertes en degré de liberté. Généralement, si l'équation est bien spécifiée, les valeurs des deux statistiques, R² et R²-ajusté, sont proches.

b. Tests de stabilité du modèle

Dans le but de faire de bonnes prévisions, les tests de stabilité sont importants pour compléter la série des tests économétriques. Pour étudier la stabilité du modèle, nous avons eu recours aux tests « Cusum » et « Cusum of squares » mis au point par BROWN-DURBIN et EVANS qui sont basés sur les résidus récursifs.

Cette régression récursive préconise l'interprétation graphique de la stabilité ou non d'une relation par le test des sommes cumulées des résidus (Cusum test) et le test des sommes cumulées des résidus récursifs (Cusum of squares).Ces tests se basent sur une représentation graphique de la série suivante: 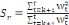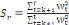,Avec : r= k+1, ..., t ; k= nombre de variables explicatives, t= nombre d'observations, et W= variable du modèle.Ainsi, l'hypothèse de stabilité du modèle est retenue si la courbe du S_r ne coupe pas les bornes qui constituent la règle de décision.

c. Tests de diagnostic sur les résidus

On distingue donc :

Ø Le test d'autocorrélation des résidus qui est conçupour vérifier si les résidus suivent un bruit blanc. Si les résidus obéissent à ce dernier, il y a absence d'autocorrélation ;

Ø Le test de normalité de Jarque et Bera qui est utilisé pour vérifier si les résidus sont normalement distribués avec les indicateurs de normalité notamment le Skewness et le Kurtosis qui mesurent respectivement l'asymétrie de la distribution autour de la moyenne et le degré d'aplatissement de la distribution ;

La série des résidus obéit ainsi à la distribution normale si la probabilité associée à la statistique de normalité des résidus est supérieure à 5%, pris comme le seuil de significativité.

Ø Le test d'héteroscédasticité de White qui permet de vérifier si le carré des résidus peut être expliqué par les variables du modèle. Dans le contexte du test d'héteroscédasticité de White, l'hypothèse nulle est que tous les coefficients de régression des carrés des résidus sont nuls, c'est-à-dire que les variables du modèle n'expliquent pas la variance des termes d'erreurs.