7.9. TECHNIQUES
D'ANALYSE DES DONNÉES
Il sera fait étalage dans cette partie de tous les
outils qui ont été utilisés pour le traitement et
l'analyse des résultats. Il semble tout de même utile de rappeler
que les données de la présente étude sont essentiellement
quantitatives.
7.9.1. Techniques
de traitement et d'analyse des données
Les techniques de traitement et d'analyse des données
dépendent de la nature des variables, du modèle de recherche et
des hypothèses de recherche. Compte tenu de l'effectif de
l'échantillon, les traitements informatiques ont semblé les mieux
adaptés pour l'opération, car« Non seulement ils
facilitent le travail et assurent une haute précision, mais ils
augmentent considérablement les possibilités du
chercheur » (De Landsheere, 1976 ; cité par Mvomo, 2011).
7.9.2. Programmes
informatiques
Après codification du questionnaire, les données
ont été insérées dans le logiciel SPSS (Version IBM
SPSS statistics21) à l'effet de procéder aux traitements et
analyses. Ce logiciel a permis de générer les tableaux
statistiques qui ont ensuite été transmis dans le logiciel Excel
2013 pour la confection des graphiques (diagrammes en secteurs et diagrammes en
bâtons).
7.9.3. Analyse
inférentielle
L'analyse statistique inférentielle a pour but de
mettre en relation deux variables afin de voir si les deux variables sont
corrélées; c'est-à-dire s'il existe un lien significatif
entre les deux. En d'autres termes, il est question de voir si la variation de
l'une des variables influence la variation de l'autre. Divers tests
non-paramétrique sont habituellement utilisés dans de tels cas.
Mais dans ce cas, compte tenu du fait que les variables sont
catégorielles, il sera fait usage du test de Khi-2.
7.9.4. Technique du
Khi-carré
La présente étude est de type descriptif et
corrélationnel. Il est donc question pour l'essentiel de montrer la
relation qui existe entre deux variables. Pour ce faire, il sera
procédé à un test d'hypothèse en faisant usage du
Khi carré. Il va permettre au cours du travail de rechercher le rapport
entre variable indépendante et variable dépendante des
hypothèses de recherche. Le test du khi carré permet donc de
mesurer l'écart qui existe entre les fréquences observées
et les fréquences théoriques. Il comporte une succession
d'étapes à savoir : la construction du tableau de
contingence, le calcul du Khi-carré, le calcul du degré de
liberté, le calcul du coefficient de contingence et la prise de
décision.
v Tableau de contingence
C'est un tableau à double entrée, qui comporte
autant de colonnes que la première variable a de modalités et
autant de lignes que la deuxième variable a de modalités.
Lesdites lignes et colonnes forment des cases dans lesquelles sont inscrites
les effectifs des sujets suivants une certaine logique. Ainsi, pour chaque
tableau de contingence, on note les fréquences observées (fo) qui
s'obtiennent en croisant les deux variables et les fréquences
théoriques (fe) qui s'obtiennent grâce à la formule
suivante :
fe = 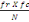 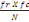 où fr = total des fréquences qui se situent sur les
rangées, fc = total des fréquences des colonnes, N= Effectif
total de l'échantillon.
v Calcul du Khi-carré
Le Khi-carré est calculé à partir des
fréquences obtenues et des fréquences théoriques
espérées. Il est la somme de chaque résidu (occurrence
observée - occurrence attendue) mis au carré divisé par
l'occurrence attendue. La formule est la suivante:
÷2 = ? 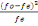 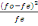 où fo= fréquence observée et fe= fréquence
théorique attendue
Si une seule des fréquences théoriques
présente une valeur inférieure à 5, on procède
à la correction de Yates dont la formule est la suivante:
÷2 = ? 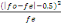 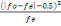 où --0,5 = Correction de Yates
v Degré de liberté (ddl)
Le degré de liberté s'obtient comme suit :
Ddl= (r-1) (c-1) où r = nombre de rangées et c=
nombre de colonnes.
v Coefficient de contingence (C)
Le coefficient de contingence permet de décrire le
degré d'association entre des variables qualitatives dans une table de
contingence. Il s'obtient grâce à la formule suivante:
|
C=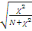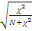  
|
Si C = 1 le lien entre les variables est Parfait
Si C > 0,8 le lien entre les variables est Très fort
Si 0,5 < C = 0,8 le lien entre les variables est Forte.
Si 0,2< C = 0,5 le lien entre les variables est Moyen
Si 0<C = 0.2 le lien entre les variables est Faible
Si C = 0 le lien entre les variables est Nul
|
v Prise de décision
Après le calcul du Khi carré, il faut
évaluer l'hypothèse par la prise de décision. Il s'agit
d'accepter ou de rejeter l'hypothèse nulle d'interdépendance
entre les variables. Il est nécessaire de fixer la probabilité
á(seuil de signification) de commettre une erreur dite
de première espèce. En général á est
égal à 5% en sciences sociales.
La valeur du X2 critique noté
X2écrit ou X2lu est lue sur
une table de distribution du Khi-carré en croisant la valeur
hypothétique á et le degré de liberté ddl de
l'étude en question. La prise de décision est la suivante :
· Si X2cal =
X2lu, on accepte l'hypothèse nulle, ce qui veut
dire que l'hypothèse de recherche est à rejeter. On conclut donc
qu'il n'existe pas un lien significatif entre les deux variables.
· Si X2cal = X2lu,
on rejette l'hypothèse nulle et on accepte l'hypothèse de
recherche. On conclura donc qu'il existe un lien significatif entre les deux
variables.
| 
