4.2 Méthode des différences finies
La méthode des différences finies peut
être utilisé pour évaluer les produits
dérivés à travers la résolution de
l'équation aux dérivées partielles (EDP), satisfaite par
le prix de ces actifs. Pour cela l'EDP est convertie en un ensemble
d'équation de différence, ces équations sont ensuite
résolues de manière itérative.
Dans cette section, nous allons appliquer la méthode
des différences finies pour l'évaluation d'options
Américaine sur devises. Cette option doit vérifier l'EDP
(2.15),déjà démontrée plus haut:
a at f + (rd - rf )S a f (4.1)
aS + 1 2cT2S2 a2
f
aS2 = rd f
Discrétisation
Considérons tout d'abord un maillage en espace (qui
représente le prix du sous-jacent) et en temps, nous nous en servons
pour écrire le schéma numérique nécessaire à
la résolution.
Discrétisation en temps
La durée de vie de l'option, T, est
divisée en N intervalles de durées:
T
L\t = N
Nous avons donc:
tn = nL\t Vn E [0, N]
Discrétisation en espace
Notons Smax un taux de change suffisamment
élevé pour qu'une fois celui-ci atteint, l'option n'ait
virtuellement aucune valeur. L'intervalle [0, Smax]
est aussi divisé en M intervalles de longueur:
Smax
L\S = M
On considère donc M + 1 taux de change
régulièrement espacés:
Sn = nL\S Vn E [0, M]
La valeur de Smax doit être choisie
de façon que l'un de ces taux de change soit le taux de change spot de
la devise sous-jacente.
Schéma numérique
Les dates et les taux de change définissent une grille
de dimension (N + 1) x (M + 1),
représentée dans la figure 4.1. Le point (i, j)
de la grille correspond à la date iL\t et au taux de
change jL\S, et fi,j désigne la
valeur de l'option en ce point.
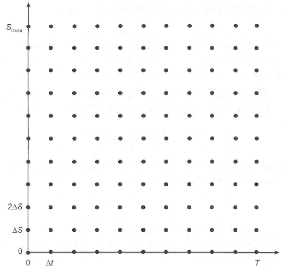
FIGURE 4.1 - Représentation du schéma
numérique de résolution, [14].
Schéma explicite des différences
finies
Dans le schéma explicite, pour tout point intérieur
(i, j) de la grille, on peut approximer af/aS
par :
af aS
fi+1,j+1 - fi+1,j-1 =(4.2)
20S
L'approximation de a2f
/aS2 par différences finies peut être
donnée par :
|
a2f
aS2 =
|
fi+1,j+1 - 2fi+1,j
+ fi+1,j-1 (4.3)
20S2
|
Pour af/at l'approximation suivante est retenue
:
|
af at
|
fi+1,j - fi,j
=(4.4)
0t
|
En substituant les équation (4.2), (4.3) et (4.4) dans
l'équation aux dérivées partielles (4.1) et en remarquant
que S = j0S, on obtient
fi+1,At f +
(rd - rf )j0Sfi+1,j+20S -1
+1
02j20S2 fi+1,j+1
- 220S2j rdfid
j
pour j = 1,2, , M - 1 et i = 0,1, ,
N - 1.
Un réarrangement des termes conduit à :
fi,j = aj
fi+1,j-1 + bj
fi+1,j + cj fi+1,j+1
(4.5)
avec :
aj = 1 + r0t(-
12(rd-rf)j0t+12~2j20t)
39
( )
1
bj = 1 -
ó2j2Lt
1 +
rLt
cj =
1 (1 )
2(rd - rf )jLt + 1
2ó2j2Lt
1 + rLt
La figure 4.2 représente la différence entre le
schéma explicite et le schéma implicite.
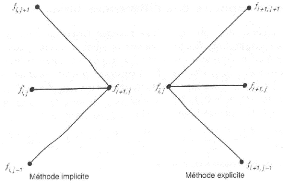
FIGURE 4.2 - Différence entre le schéma implicite
et le schéma explicite.
Le schéma implicite donne une relation entre trois
valeurs différentes de l'option à la date iLt qui sont
fi,j-1, fi,j et
fi,j+1, et une valeur de l'option à
la date (i + 1)Lt qui est fi+1,j.
Par contre, le schéma explicite donne une relation entre la valeur
de l'option à la date iLt qui est fi,j et
trois valeurs différentes de l'option à la date (i +
1)Lt qui sont fi+1,j-1, fi+1,j
et fi+1,j+1
L'avantage de la méthode implicite est qu'elle est
indéfiniment stable, mais elle nécessite la résolution
d'un système de M - 1 équation, à chaque pas du
temps, afin de déterminer la valeur de fi,j
à partir des fi+1,j. Pour cette
raison on a choisi d'utiliser la méthode explicite afin de simplifier
les calculs, mais cette méthode nécessite une étude de
stabilité.
Conditions initiales et aux limites
Conditions initiales
Puisque nous avons utilisé un schéma
rétrograde, la condition initiale correspond à la condition
à la date d'expiration de l'option.
-- Pour un call : À la date t =
T on a :
fN,j = max(S - K;0)
= max(jLS - K;0) j = 0,1, , M
(4.6)
-- Pour un put : À la date t =
T on a :
fN,j = max(K - S;0)
= max(K - jLS;0) j = 0,1, , M
(4.7)
40
Conditions aux limites
On suppose qu'il n'existe pas de convexité aux bords, de
sorte que les valeurs aux bords n'affectent pas les calculs de manière
significative, on impose pour cela les conditions Zero-Gamma aux deux
extrémités de l'espace, on a : ?2 f
?S2 = 0 pour j = 0 et j = M,
on aura donc:
fi,0 - 2 fi,1 +
fi,2 = 0 (4.8)
fi,M-2 - 2fi,M-1 +
fi,M = 0 (4.9)
Formulation matricielle
Afin d'implémenter le code de résolution
numérique de l'EDP avec le schéma explicite, il nous faut tout
d'abord faire la formulation matricielle de l'équation (4.5).
La formulation matricielle de l'équation (4.5) et des
condition initiales et aux bords est donnée par:
Fi = AFi+1 + Ki+1 (4.10)
?
? ? ? ? ? ?
Avec i = 0,1, , N - 1 et
fi,1
Fi =
fi,2
...
..
.
i,M-1
|
Ki+1 =
|
?
? ? ? ? ? ?
|
a1 fi+1,0
0
...
...
cM-1 fi+1,M
|
?
? ? ? ? ? ?
|
A = ? 0 a3 b3 ···
··· 0 0
?b1 c1 0 ···
··· 0 0
? ? a2 b2 c0 ···
··· 0 0
? ? .
? .. ....
0 0 0 · · · ··· aM-1
bM-1
. . ....
. ..
. . ... ?
? ? ? ? ? ?
Stabilité et convergence
La méthode de différences finies traitée
ci-dessus est stable et fiable sous certaines conditions. En effet, pour une
équation aux dérivées partielles bien posée, un
schéma d'approxi-mation numérique convergent nous donnera sa
vraie solution, tant que le schéma est stable. Les paragraphes suivants
décrivent ce que l'on entend par chacun de ces termes techniques:
schéma numérique bien posé, convergent et stable.
Il faut d'abord déterminer si le problème
mathématique pour lequel une solution est recherchée a non
seulement une solution, mais aussi si cette solution est facile à
trouver. On sait qu'un tel problème est bien posé, et ces
problèmes ont généralement une solution qui change peu
lorsqu'on se déplace dans son voisinage à petits pas . Les
mathématiciens appellent cela stable sous l'effet de petites
perturbations. Le fait que notre problème de pricing des options
est bien posé est intuitivement évident:
L'économie derrière nous dit qu'il n'y aura qu'un seul prix pour
le contrat d'option à un et ce prix évoluera lentement en
fonction des petites variations des variables économiques.
Un schéma numérique est dit convergent si, au
fur et à mesure que la taille du maillage et les tailles des pas de
temps diminuent, le schéma de différences finies se rapproche de
plus en plus des équations différentielles qui tentent de
l'approcher. Nous avons donc choisi une bonne discrétisation du
problème considéré. C'est également le cas pour le
schéma de différences finies explicite pour déterminer les
prix des options ci-dessus. Au fur et à mesure que la taille des pas
devient de plus en plus petite, nos approximations des dérivés
s'améliorent.
En passant du problème à la méthode
d'approximation que nous adoptons, nous trouvons que les idées de
stabilité sont également importantes. La stabilité d'une
méthode d'approxi-mation mise en oeuvre fait référence
à l'impact que de petites erreurs dans la méthode ont sur les
résultats. Si ces petites erreurs peuvent produire de grandes
fluctuations dans les résultats - en déplaçant la solution
approximative loin de la vraie solution - alors la méthode a une faible
stabilité. Un système de différences finies efficace doit
donc satisfaire les conditions de stabilité.
Lemma 4.2.1. On peut montrer que le
schéma explicite des différences finies est stable ssi
0 < (ÄS)2 = 1
Ät
2
Lemma 4.2.2. On peut montrer que le
schéma implicite des différences finies est stable ssi
Ät
0 < (ÄS)2
D'après le lemme 4.2.1 et le lemme 4.2.2, nous savons
que la méthode implicite est toujours stable pour l'EDP de Black-Scholes
car Ot et OS sont tous deux positifs, mais la méthode
explicite n'est pas toujours stable. Ainsi, la stabilité et la
précision de ces deux méthodes à différences finies
exigent que ces conditions soient satisfaites pour les valeurs assez petites de
Ot et OS.
Résolution
Pour évaluer les options Américaines à
l'aide de la méthode des différences finies nous devons faire
respecter l'exigence selon laquelle, à chaque noeud, la valeur de
l'option est supérieure à son payoff (valeur
intrinsèque) à cet instant.
Cas d'un call
La valeur d'un call Américain, à chaque instant
i, doit vérifier la condition suivante:
fi,j ~ max(jÄS -
K;0)
car sinon, l'exercice à la date à la date T
- iÄt est optimal. Donc:
fi,j = max(max(jÄS
- K;0); aj fi+1,j-1 +
bj fi+1,j + cj
fi+1,j+1)
41
42
Cas d'un put
La valeur d'un put Américain, à chaque instant
i, doit vérifier la condition suivante:
fi,j = max(K -
jÄS;0)
car sinon, l'exercice à la date à la date T
- iÄt est optimal. Donc:
fi,j = max(max(K - jÄS;
0); aj fi+1,j-1 + bj
fi+1,j + cj
fi+1,j+1)
| 


