I.2 Spécification
théorique du modèle Logit
Le modèle logit a une double nature. D'une part, c'est
un modèle de régression où la variable dépendante
est binaire. D'autre part, c'est une méthode alternative à
l'analyse discriminante linéaire. Par ailleurs, le modèle logit
peut aussi être considéré comme un modèle
économique de choix discrets.
Les modèles Logit depuis très longtemps ont
été introduits comme des approximations de modèles probit
permettant des calculs plus simples. Si les deux modèles sont
sensiblement identiques, il existe cependant des différences. Nous
évoquerons ici les principales différences :
· Les modèles Logit sont construits sur
l'hypothèse des distributions cumulatives logistiques permettant un
traitement plus adéquat des données aberrantes du fait de leurs
extrémités épaissies contrairement aux modèles
Probit qui font l'hypothèse d'une distribution cumulative normale
centrée réduite ;
· Dans les modèles complexes, les modèles
Logit sont plus adaptés parce que sont de manipulation plus
aisée, car le Probit impliquerait la manipulation des intégrales
à plusieurs degrés. Les bases théoriques des
modèles Logit ont été données par Mc Fadden
à travers une théorie de l'utilité.
I.3 Procédure
d'estimation
La méthodologie empirique utilisée dans cette
étude se déroule en quatre étapes et consiste à
déterminer le degré de significativité de chacune des
variables. Pour vérifier la significativité individuelle des
paramètres, le test de Student sera utilisé. L'hypothèse
de nullité du vecteur des paramètres quant à elle sera
testée par le test du rapport de maximum de vraisemblance. Pour
évaluer la qualité des ajustements, nous aurons recours au Psudo
R² de McFadden. En outre, le pourcentage de bonne prédiction nous
permettra de juger du pouvoir prédictif du modèle. Les valeurs
numériques des coefficients du Logit n'ont pas d'interprétation
directe c'est pourquoi nous allons nous intéresser aux signes des
variables pertinentes et aux réactions proportionnelles de la variable
expliquée suite aux changements proportionnels du niveau des variables
explicatives c'est à dire aux élasticités. La variable
endogène dans notre cas étant une probabilité, le calcul
des effets marginaux permet d'apprécier l'impact des variables
explicatives sur la probabilité d'être ou non en
l'insécurité alimentaire.
I.3.1 Vraisemblance du
modèle
Pour vérifier la significativité globale du
modèle, des tests de vraisemblance sont réalisés. Plus la
vraisemblance est élevée, plus le modèle est
considéré comme adéquat pour expliquer les variations de
la variable dépendante. Le test de vraisemblance d'un modèle
consiste à déterminer s'il existe au moins un coefficient non nul
parmi ceux des variables explicatives insérées dans le
modèle. Si c'est le cas, on peut considérer que le modèle
est globalement significatif, et s'intéresser alors aux variables qui
influencent effectivement la variable dépendante qu'on cherche
prédire. La vraisemblance d'un n-échantillon
y1,y2,...,yn est définie comme la
probabilité d'observer cet échantillon.

· Les variables Yi étant indépendantes:

Avec 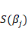 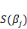 tel que tel que  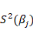 soient les variances des estimateurs telles que la matrice de variance
covariance soit de la forme : soient les variances des estimateurs telles que la matrice de variance
covariance soit de la forme :
 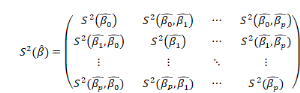
| 


