I.3.2 Intervalles de
confiance
Ce test permet de savoir s'il y a une relation entre la
variable Xj et Y.
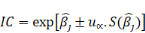 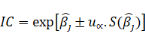
v Si 1 n'appartient à IC : pas de relation
v Si 1 appartient à IC : relation entre Xj et Y
I.3.3 Test de
significativité globale
Ce teste a pour objectif de voir si les variables explicatives
peuvent expliquer le risque de survenue de l'évènement. On va
alors faire un test de rapport de vraisemblance.
On appelle M1: Modèle sans variables et M2:
Modèle avec toutes les variables
On teste :
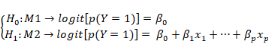
v Est-ce que M1 est meilleur que M2 (qualités
prédictives)?
v La statistique de test est:
ü RV= [-2.ln (vraisemblance au maximum de M1)] -
[-2.ln(vraisemblance au maximum deM2)]
ü Et suit un Khi-deux à p
degrés de liberté
ü Si RV > ÷²(p) On rejette H0, le
modèle 2 est meilleur que le 1, les variables explicatives ont
simultanément une influence sur la probabilité d'apparition de
l'évènement étudié.
I.3.4 Test de
significativité pour une variable
· M1: Modèle sans la variable testée 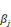 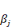
· M2: Modèle avec la variable testée 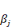 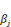
· On teste:
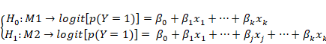
C'est-à-dire : 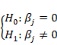 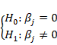
· Il y a 2 manières d'écrire la statistique
de test :
ü Sous une loi Normale:
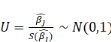 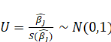 Sous H0 Sous H0
ü Sous une loi du Khi-deux:
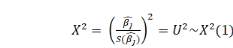 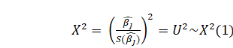 Sous H0 Sous H0
· Sous une loi Normale:
Si |U| > N(0,1) (=1,96 à
95%)
· Sous une loi du Khi-deux:
Si U > ÷²(1)
On rejette HO, le modèle 2 est meilleur que
le 1, le paramètre 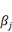 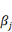 est significatif, la variable j a une influence sur la
probabilité d'apparition de l'évènement, sachant les
autres variables du modèle. est significatif, la variable j a une influence sur la
probabilité d'apparition de l'évènement, sachant les
autres variables du modèle.
I.3.5 Qualité de
l'ajustement du modèle
Le pseudo R² de Mac Fadden renseigne sur la
qualité d'ajustement du modèle, c'est-à- dire sur la
capacité des variables explicatives étudiées à
prédire les variations de la variable dépendante. Un pseudo
R² proche de 0 indique que les variables explicatives n'apportent que peu
d'informations tandis qu'un pseudo R² proche de 1 souligne l'importance
des variables explicatives. Pour les régressions multinomiales non
ordonnées, on considère en général qu'un pseudo
R² de 30% indique que le modèle étudié a un bon
pouvoir prédictif. Pour les régressions multinomiales
ordonnées, les pseudo R² sont plus faibles et des valeurs autour de
10% suffisent pour considérer que les variables explicatives contribuent
de façon significative à expliquer les variations
observées de la variable à expliquer.
| 


