INTRODUCTION
À l'échelle globale, les causes structurales de
l'insécurité alimentaire sont de nature politique et
économique, telles que les politiques en matière de production
alimentaire, de prix des aliments, de logement, de transport et d'emploi. Il a
été largement documenté que dans les pays
développés l'insécurité alimentaire des
ménages pourrait être modulée par différents
facteurs de l'environnement physique et social, de l'environnement familial et
individuels. En premier lieu, les facteurs de l'environnement physique et
social comme; le manque de transport, la distribution des ressources
alimentaires, les caractéristiques (prix, qualité,
variété) de l'offre alimentaire dans les magasins et le soutien
social, influencent l'insécurité alimentaire des ménages.
En deuxième lieu, certaines caractéristiques du ménage
augmentent le risque d'être en insécurité alimentaire,
notamment; le revenu, la monoparentalité (spécialement lorsque le
chef du ménage est une femme), le nombre de membres dans le
ménage, les dépenses du foyer, et le manque d'équipement
ménager. Finalement, l'insécurité alimentaire a
été associée aux caractéristiques individuelles
telles que : un faible niveau de scolarité, le fait d'être une
femme, un mauvais état de santé, l'appartenance à une
communauté ethnique minoritaire, les connaissances en alimentation et
nutrition et la capacité de cuisinier. Dans ce travail, nous cherchons
à identifier les déterminants de la sécurité
alimentaire en RCA. Dans la première section, nous présentons le
model d'analyse utilisée pour mener notre étude et nous allons
présenter ensuite dans la seconde section, les variables et les
données utilisées pour l'application empirique.
I. CADRE ANALYTIQUE DU MODEL
LOGIT
La régression logistique est l'un des modèles
d'analyse multivariée les plus couramment utilisées en
épidémiologie. Elle permet de mesurer l'association entre la
survenue d'un événement (variable expliquée qualitative)
et les facteurs susceptibles de l'influencer (variables explicatives).
I.1 Nature du modèle
économétrique
Historiquement, la régression logistique ou
régression binomiale fut la première méthode
utilisée, notamment en épidémiologie et en marketing
(scoring), pour aborder la modélisation d'une variable binaire binomiale
(nombre de succès pour ni essais) ou de Bernoulli (avec ni =1) :
décès ou survie d'un patient, absence ou présence d'une
pathologie, possession on non d'un produit, bon ou mauvais client... Bien
connue dans ces types d'application et largement répandue, la
régression logistique conduit à des interprétations
pouvant être complexes mais rentrées dans les usages pour
quantifier, par exemple, des facteurs de risque liés à une
pathologie, une faillite... Cette méthode reste donc celle la plus
utilisée car interprétable même si, en terme de
qualité prévisionnelle, d'autres approches sont susceptibles, en
fonction des données étudiées, de conduire à de
meilleures prévisions. Enfin, robuste, cette méthode passe
à l'échelle des données massives. Il est donc important de
bien maîtriser les différents aspects de la régression
logistiques dont l'interprétation des paramètres, la
sélection de modèle par sélection de variables ou par
régularisation (Lasso).
I.1.1 Approche descriptive
On observe un échantillon d'individus dont on connait K
de leurs caractéristiques, représentées par les K
variables x1, x2, ..., xK. . On suppose que
les individus sont répartis en deux catégories C0 et
C1. En RCA, une partie de la population (fait partie de la
catégorie C1 des personnes en sécurité
alimentaire), d'autres pas (catégorie C0 des personnes en
insécurité alimentaire). On souhaite analyser et quantifier le
lien existant entre les caractéristiques individuelles xk et
l'appartenance à C0 ou C1. Il faut un outil - un
modèle - spécifique pour pouvoir le faire. C'est dans cette
logique qu'on a choisi le model de Régression logistique (logit).
On part donc du principe que la population que l'on
étudie est scindée en deux catégories, C0 et
C1. On dispose d'un échantillon de n individus indicés
par i, représentatifs de cette population. On connait K
caractéristiques de ces individus, mesurées par les variables
x1 x2, . . ., xK. Pour l'individu i, les K
variables prennent les valeurs x1i, x2i, . . . ,
xKi. On pose que la probabilité P que l'individu i (compte
tenu de ses caractéristiques x1i, x2i, ...,
xKi) appartienne à C1 ou à C0
est une fonction des x1i, x2i, ..., xKi. On
précise un peu la relation fonctionnelle en supposant que les
probabilités d'appartenance dépendent d'une combinaison
linéaire des caractéristiques. Formellement, cela s'écrit
:
 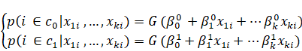 (1) (1)
ou G est une fonction qui sera définie
ultérieurement et ou les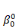  , ,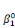 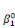 , . . ., , . . ., 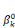 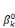 , et les , et les 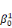 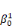 , , 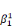 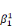 , . . ., , . . ., 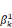 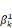 , sont les coefficients des combinaisons linéaires. Ce sont les
paramètres du modèle. On notera l'ajout des deux
paramètres , sont les coefficients des combinaisons linéaires. Ce sont les
paramètres du modèle. On notera l'ajout des deux
paramètres 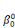 , et , et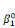 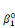 , qui sont appelés parfois paramètres du « terme
constant ». Ils sont associés à la variable x0
valant systématiquement 1. A ce stade, on a donc deux séries de
paramètres âkJ : , qui sont appelés parfois paramètres du « terme
constant ». Ils sont associés à la variable x0
valant systématiquement 1. A ce stade, on a donc deux séries de
paramètres âkJ :
· la série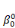 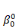 , , 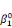 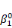 ,, . . ., ,, . . .,  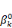 , associée à la catégorie C0 (j = 0) ; , associée à la catégorie C0 (j = 0) ;
· la série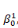  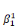  , . . ., , . . ., 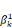 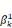 , associée à la catégorie C1 (j = 1). , associée à la catégorie C1 (j = 1).
La combinaison linéaire des caractéristiques
peut s'écrire de manière synthétique, pour j = 0 ou j = 1
:
 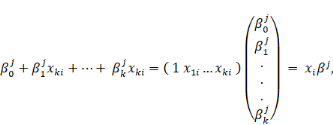 (2) (2)
Ou xi = (1x1i . . . xKi) est le
vecteur-ligne des caractéristiques de l'individu
i et
ßj le vecteur-colonne 4 des paramètres du
modèle. On peut alors réécrire (1) de
manière
condensée :
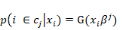  Pour j= 0,1. Pour j= 0,1.
Quelle fonction choisir pour G 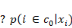 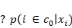 et et  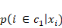 étant des probabilités, on doit avoir : étant des probabilités, on doit avoir :
 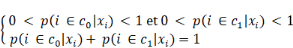 (3) (3)
Poser 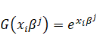 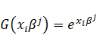 assurerait assurerait   > 0. Mais les autres contraintes ne seraient pas
vérifiées. Pour qu'elles le soient, il suffit de normer les deux
quantités > 0. Mais les autres contraintes ne seraient pas
vérifiées. Pour qu'elles le soient, il suffit de normer les deux
quantités 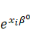 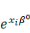 et et 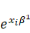  , c'est-`a-dire les diviser par leur somme. On obtient alors : , c'est-`a-dire les diviser par leur somme. On obtient alors :
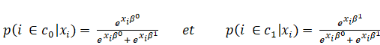 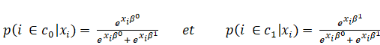
C'est cette forme fonctionnelle qui donne au modèle son
nom de logit. On peut simplifier en remarquant qu'une seule probabilité
suffit pour le représenter, puisque la somme de 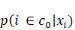 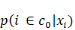 et de et de 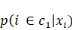  est égale à 1. L'une se déduit de l'autre. On se
centre sur la probabilité d'appartenir à C1. Elle
s'écrit : est égale à 1. L'une se déduit de l'autre. On se
centre sur la probabilité d'appartenir à C1. Elle
s'écrit :
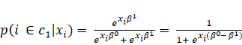 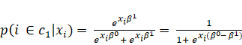
Finalement, si on pose â = â1 ?
â0, on a :
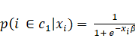 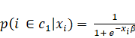 (4) (4)
| 


