IV.3. LA CORRELATION ENTRE LES
DEUX GESTIONS
La gestion de MS et celle de la RH va de pair en paire parce
que toutes deux dépendent de la production due à l'entreprise. En
cas d'une chute de la production la masse salariale diminue et la gestion des
ressources humaines réduit son effectif, dans le cas contraire
c'est-à-dire, lorsqu'il y a augmentation de la production elles
augmentent encore ensemble.
Tableau N°15 : De la corrélation
entre la MS et la GRH (effectif).
|
Année
|
Masse Salariale
|
Gestion des RH (effectif)
|
|
2015
|
172.198.600
|
4.500
|
|
2016
|
86.099.300
|
2.500
|
|
2017
|
258.297.900
|
4.500
|
|
2018
|
258.297.900
|
4.500
|
|
2019
|
258.297.900
|
4.500
|
Source : GRH système
KCC
Ici nous avons le tableau des données chiffrées
de nos deux gestions sous-examen celles des masses salariales et des effectifs
desdifférentes années.
IV.3.1. La corrélation desgraphiques de la
masse salariale et de l'effectif
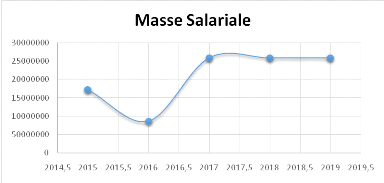
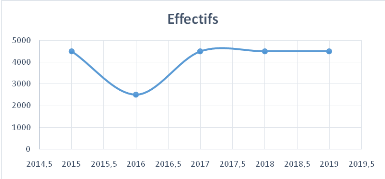
Les deux graphiques ci-dessus nous fait voir la
corrélation qui a entre l'effectif et la gestion de la masse salariale
de 2015 à 2019, une légère différence se fait
remarquée entre les deux du fait qu'après la chute due à
la production de 2016 qui avait obligée l'entreprise à
diminuée son effectif, cette dernière a recourue au recrutement
remettant son personnel au même effectif que celui de 2015 bien que sa
masse salariale soit plus élevée que celle-ci.Au lieu de recruter
un personnel plus que celui de 2015, l'entreprise a optée pour
l'augmentation des heures de prestation et revoir à la hausse le salaire
de son personnel.
NB : la gestion de la masse salariale consiste
donc à la fois à faire la gestion financière et la gestion
du personnel.
IV.3.2 La régression linéaire
simple
Tableau N°16 de Modèle :
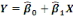 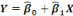
|
N°
|
X
|
Y
|
Y-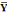 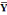
|
X- 
|
Yi(X-  ) )
|
X(X-  ) )
|
(X-  )2 )2
|
(X-  ) (Y- ) (Y-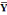  ) )
|
|
1
|
4,5
|
172198,6
|
-34 439,72
|
0,4
|
68 879,44
|
1,8
|
0,16
|
-13 775,90
|
|
2
|
2,5
|
86099,3
|
-120 539,02
|
-1,6
|
-137 758,88
|
-4
|
2,56
|
192 862,43
|
|
3
|
4,5
|
258 297,9
|
51 659,58
|
0,4
|
103 319,16
|
1,8
|
0,16
|
20 663,83
|
|
4
|
4,5
|
258 297,9
|
51 659,58
|
0,4
|
103 319,16
|
1,8
|
0,16
|
20 663,83
|
|
5
|
4,5
|
258 297,9
|
51 659,58
|
0,4
|
103 319,16
|
1,8
|
0,16
|
20 663,83
|
|
?
|
20,5
|
1 033 191,6
|
0
|
0
|
241 078,04
|
3,2
|
3,2
|
241 078,04
|
Source : conception personnelle
  = =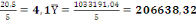 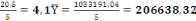
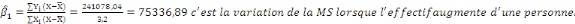 a) a) 
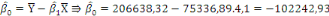 b) b) 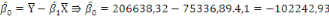
 c) c) 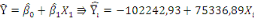

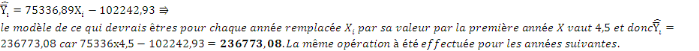 v v 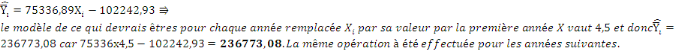
Tableau N°17 : suitede Modèle :
 
|
N°
|
|
Y- 
|
(Y-  )2 )2
|
(Y-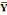  )/ )/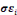 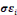
|
(Y-  )2 )2
|
|
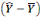 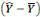 2 2
|
|
1
|
236 773,08
|
-64574,5
|
4 169 866 050
|
-1,5
|
1 186 094 314
|
30 137,76
|
908 103 760,26
|
|
2
|
86 099,3
|
0
|
0
|
0
|
14 529 655 342,56
|
-120 539,02
|
14 529 655 342,56
|
|
3
|
236 773,08
|
21524,8
|
463 317 015
|
0,50
|
2 668 712 205,78
|
30 137,76
|
908 103 760,26
|
|
4
|
236 773,08
|
21524,8
|
463 317 015
|
0,50
|
2 668 712 205,78
|
30 137,76
|
908 103 760,26
|
|
5
|
236 773,08
|
21524,8
|
463 317 015
|
0,50
|
2 668 712 205,78
|
30 137,76
|
908 103 760,26
|
|
?
|
1 033 191,62
|
|
5 559 817 095
|
0
|
23 721 886 274
|
|
18 162 070 384
|
Source : conception personnelle


Coefficient de correction :   L'effectif et la MS sont en corrélation à 88%.
C'est-à-dire que nous avons un bon modèle estimatif. L'effectif et la MS sont en corrélation à 88%.
C'est-à-dire que nous avons un bon modèle estimatif.
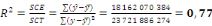  Le coefficient de détermination (R2)
vaut 77%. Alors 77% de la variabilité de la masse salariale
estexpliquée par l'effectif. Le coefficient de détermination (R2)
vaut 77%. Alors 77% de la variabilité de la masse salariale
estexpliquée par l'effectif.
Test d'hypothèse : le
modèle est-il globalement significatif ?
Le principe : si Fisher calculé est
supérieur au Fisher Théorique on rejette l'hypothèse
nulle.
H0 : le modèle n'est pas globalement
significatif.
H1 : le modèle est globalement
significatif.
Fisher theories (2,3) = 9,55
Fisher calculé=  
Puisque le Fisher Calculé est à supérieur
Fisher Théorique, on rejette l'hypothèse initiale et donc le
modèle est globalement significatif. Ceci implique que l'effectif a une
influence sur la masse salariale.
Tableau N°18 : d'ANOVA
|
Source de variation
|
Somme de carré
|
Degré de liberté
|
Carré moyen
|
|
Régression
|
18 162 070 384
|
1
|
18 162 070 384
|
|
Résiduelle
|
5 559 817 085
|
3
|
1 853 272 365
|
|
Total
|
23 721 886 274
|
4
|
5 930 471 569
|
Source : conception
personnelle
Le tableau d'analyse de la variance se présente de la
manière décrite ci-haut, nous avons la somme de carré due
à la régression qui correspond à   2 et vaut/18 162 070 384, son degré de
liberté est de 1. Ensuite nous avons la somme de carré
résiduelle (? 2 et vaut/18 162 070 384, son degré de
liberté est de 1. Ensuite nous avons la somme de carré
résiduelle (? 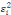 ) 5 559 817 085, son degré de liberté est de 3
et enfin nous avons la somme de carré total ) 5 559 817 085, son degré de liberté est de 3
et enfin nous avons la somme de carré total  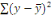 de 23 721 886 274 avec comme degré de liberté
4. de 23 721 886 274 avec comme degré de liberté
4.
|
|



