3-2-3-2 : Le modèle 2, modèle de
l'investissement privé
3-2-3 -2-1 Estimation de la relation de long
terme du modèle 1
L'estimation de notre deuxième modèle dans le
long terme nous donne l'équation ci-après (voir tableau 16
annexes) :
L(INVP)t= 3.56 +0.52
L(INVINF)+0.12L(INVEDU)+0.16L(INVAGR) -0.16L(INVSAN)
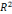  =73% =73% 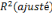  = 69% p =0.0000 DW = 1,61 N= 33 = 69% p =0.0000 DW = 1,61 N= 33
La statistique de ficher est égale à 18.89 et
sa probabilité est presque nulle. Ce qui permet de dire que le
modèle est globalement significatif. Les tests de diagnostics sur les
erreurs ont été concluants)au seuil de 5% (voir les tableaux
en annexes): les erreurs suivent une loi normale ( test de Jarques Bera), elles
sont homoscédastiques (test de White) et non
auto-corrélées ( test de Breuch Godfrey) car les
différentes probabilités associées a ces tests sont
chacune supérieurs à 5%. Le modèle est stable (test de
Cusum). (voir les différents tests sur le modèle 2 dans le long
terme en annexes).
Eu égard au coefficient de déterminant
ajusté 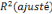 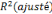 nous pouvons dire que 69% des fluctuations du PIB sont expliques par le
modèle. nous pouvons dire que 69% des fluctuations du PIB sont expliques par le
modèle.
A partir du tableau 16 (en annexes) on observe que les
investissements publics en général ont des effets
considérables sur la productivité privée et en particulier
celles des infrastructures qui agissent positivement et significativement sur
la croissance économique en plus de celles de l'agriculture, ce qui
concorde avec les travaux de Barro (1991). Mais on observe une relation de
négativité entre l'investissement privée et les
investissements en capital humain ce qui confirme nos résultats dans
l'estimation de la première équation du modèle 1,
l'absence d'improductivité n'encourage pas les privées d'investir
dans le domaine social (éducation, santé).
Les tests de ADF et de PP sur le résidu du
modèle montrent que la série des résidus est stationnaire
(voir tableau 17 en annexes). Les variables sont donc
cointégrées, comme le confirme le test de Johansen
3-2-3 -2-2 Estimation de la relation dynamique de court
terme du modèle 2
L'estimation de notre deuxième modèle dans le
court terme nous donne l'équation suivante (voir tableau 18 en
annexes) :
D(L(INVP))=-0.15+0.24dL(INVINF)+0.09DL(INVEDU)+0.33dL(INVAGRI)-0.006dL(INVSAN)-0.61
  =63% =63%  = 55% p =0.000025 DW = 2.10 N 33 = 55% p =0.000025 DW = 2.10 N 33
Eu égard au coefficient de déterminant
ajusté 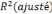  nous pouvons dire que 55% des fluctuations du PIB en court terme sont
expliquées par le modèle. nous pouvons dire que 55% des fluctuations du PIB en court terme sont
expliquées par le modèle.
La statistique de ficher est égale à 8.85 et
sa probabilité est égale 0.000052. ce qui permet de dire que le
modèle est globalement significatif. Les tests de diagnostics sur les
erreurs ont été concluants)au seuil de 5% (voir les tableaux
en annexes): les erreurs suivent une loi normale ( test de Jarques Bera), elles
sont homoscédastiques (test de White) et non
auto-corrélées ( test de Breuch Godfrey) car les
différentes probabilités associées a ces tests sont
chacune supérieurs à 5%. Le modèle est stable (test de
Cusum). (Voir les différents tests sur le modèle 2 dans le court
terme en annexes).
Les résultats de l'estimation de l'équation
donnent presque les mêmes résultats que la première
équation de long terme. On peut confirmer que les investissements en
infrastructures est la variable qui agit plus sur la productivité
privée qui est le moteur de la croissance économique. Ce qui
cadre bien avec les théories de socialistes et de keynésiennes
qui pensent que les dépenses de l'Etat ont un impact significatif sur
l'activité économique
| 


