CHAPITRE II :
MODELISATION DE LA CHAINE D'ASSERVISSEMENT D'UN MOTEUR
CC
Modélisation du MCC
Lorsque l'on veut la faire travailler, en appliquant un couple
résistant sur son axe, cela la freine donc E diminue.
Comme
U reste constante, le produit
Ri.Ii augmente donc
Ii augmente, donc le couple T augmente lui aussi
et lutte contre la diminution de vitesse : c'est un couple
moteur.
Plus on le freine, plus le courant augmente pour lutter
contre la diminution de vitesse. C'est pourquoi les moteurs à courant
continu peuvent « griller » lorsque le rotor est
bloqué, si le courant de la source n'est pas limité à une
valeur correcte.
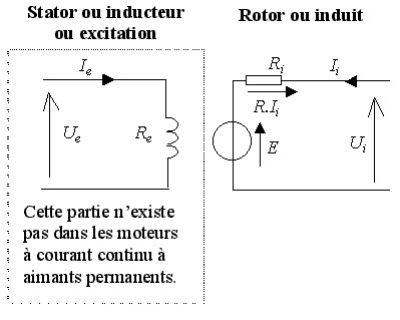
1. Modélisation par la fonction de
transfert
a-Equations électriques
La tension d'induit (en convention récepteur) :
(1)
La f.é.m : : e(t) = Ke.Ù(t)
(2)
Avec
R: résistance d'induit
L: inductance d'induit en henry
e(t): f.é.m induite
K: Constante tenant compte du flux constant
a. Equations mécaniques
Le principe fondamental de la dynamique (PFD) nous permet
d'écrire :
(3)
On a aussi : Cm=
Kc.I (4)
On suppose que le moment du couple résistant est de la
forme :
Cr = f .Ù (5)
Avec
J: moment d'inertie de l'axe du rotor en
Kg.m2
f: coefficient de frottement visqueux.
Transformation de Laplace de toutes équations
électromécanique est traduite dans ce tableau en
dessous :
a. Equations électromécaniques dans le
domaine de Laplace
La transformée de Laplace de l'équation (1) est :
U(P) = R.I(P) + L.p.I(P) + E(P)
La transformée de Laplace de l'équation (2) est :
E(P) = Ke.Ù(P) (2'), on peut alors écrire :
U(P) = (R.+ L.P)I(P) + Ke.Ù(P) (1')
La transformée de Laplace de l'équation (3) est :
J.P.Ù(P)= Kc.I(P) - Cr (3')
Et en tenant compte de l'équation (4) et (5) on peut
écrire :
J.P.Ù(P)= Kc.I(P) - f.Ù(P)  (J.P +f) .Ù(P)=
Kc.I(P)   (4')
|
Equations électromécaniques
|
N°
|
Transformée de Laplace
|
|
(1)
|
U(P) = R.I(P) + L.p.I(P) + E(P)
|
|
e(t) = Ke.Ù(t)
|
(2)
|
E(P) = Ke.Ù(P)
|
|
(3)
|
J.P.Ù(P)= Cm - Cr
J.P.Ù(P)= Kc.I(P) - f.Ù(p
|
|
Cm= Kc.I
|
(4)
|
Cm=Kc.I(P)
|
|
Cr = f .Ù
|
(5)
|
Cr=f.Ù(P)
|
Ce qui donne :
  
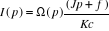
Et en remplaçant cette nouvelle expression de I(p) dans
l'équation (1') on obtient
 
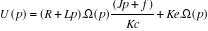
Le modèle de MCC comme suivant :
Fig. 1: Schema Bloc d'un MCC
On peut maintenant exprimer la fonction de transfert en boucle
fermée  :
 
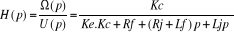
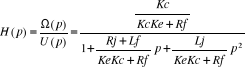
Qu'on peut écrire aussi sous la forme canonique d'une
fonction de transfert de second ordre :
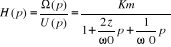
2. Modélisation par Variables
d'état
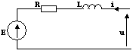
Fig.2 : Modèle équivalent de
l'induit en régime dynamique
On a :
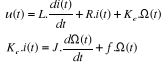
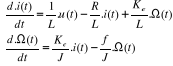
La représentation d'état :
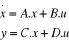
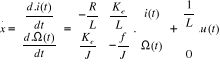
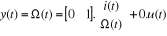
Modélisation du
hacheur
Le hacheur est composé d'un transistor en série
avec une diode tête bêche. Si le rapport cyclique est la commande
du transistor, on obtient la relation entre tension d'entrée et de
sortie suivante Umoy=.E.
Le hacheur est donc un simple amplificateur de Fonction de
Transfert : C(p)=E avec E la tension d'alimentation du
Hacheur.
á
Umoy=á.E
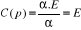
Pour que la modélisation soit réaliste, il faut
limiter la valeur de entre 0 et 1, puisque dans la réalité, le
rapport cyclique de la commande du transistor reste compris entre 0 et
Modélisation du capteur de
vitesse :
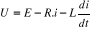
Le signal provenant du capteur de vitesse attaquera le
comparateur à base d'amplificateur opérationnel
On suppose que l'amplificateur opérationnel est
idéal
Résistance d'entrée très grande
Courant i=0
On en déduit que : U=E, or E = K.Ö.n
On met : K.Ö = KG = Constante de la dynamo
tachymétrique
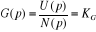
Donc U=E= KG n
D'où la fonction de transfert :
 est
donnée par le constructeur, dans notre simulation le constructeur nous
donne la valeur 0.01146
| 
