CHAPITRE I :
APPLICATION DE LA LOGIQUE FLOU
Notions d'ensemble flou, appartenance
Les compréhensions de l'univers dans lequel nous
évoluons sont généralement imparfaites dans la mesure
où elles peuvent être entachées d'incertitudes et/ou
d'imprécisions, ne serait-ce qu'à travers la perception que nous
en avons. Or, nous pouvons constater que l'homme intègre naturellement
ces imperfections dans la vie de tous les jours, en particulier au niveau du
raisonnement et de la décision. L'idée du professeur Lotfi Zadeh
à travers le nouveau concept ensembliste d'appartenance graduelle d'un
élément à un ensemble, a été de
définir une logique multi évaluée permettant de
modéliser ces imperfections c'est prendre en compte les états
intermédiaires entre le tout et le rien. L'utilité de cette
approche peut être illustrée de la manière suivante :
Une température de 10°C, pour un humain, est
généralement considérée comme froide; une autre de
40°C est qualifiée de chaude. Si chacune de ces valeurs appartient
à une
Catégorie (ensemble) bien définie, qu'en est-il
pour des valeurs intermédiaires? Une réponse intuitive consiste
à affirmer qu'elles appartiennent à une ou deux des
catégories précédentes avec des niveaux ou des
degrés (normalisés) différents. On évite ainsi des
transitions brusques entre différentes catégories, comme cela est
le cas en logique binaire (figureI.1).
Il semble en effet surprenant de considérer qu'une
température de 40°C est chaude, alors qu'une température de
39,9°C ne l'est pas.
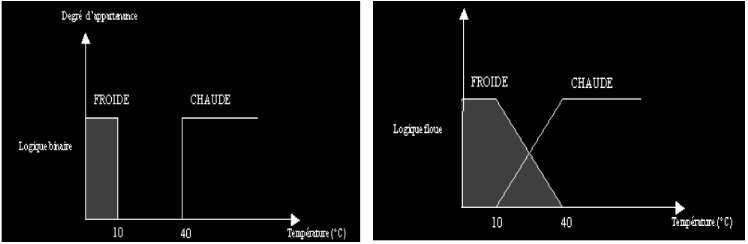
Figure I.1 : Exemple de définition d'ensembles sur un
univers de discours en logique
Binaire et en logique floue
Cet exemple permet d'illustrer le fait qu'une logique binaire
classique soit, dans certains cas, trop limitative. Donc il est
nécessaire de faire appel à une autre logique multi
évaluée qui sera vue comme une extension de la
précédente, c'est bien la logique floue.
En ce qui concerne la commande d'un processus quelconque, la
logique floue permet une approche fondatrice par rapport à l'automatique
classique. En automatique, en général, on s'attache à
modéliser le processus à travers un certain nombre
d'équations différentielles. Cette modélisation est rendue
difficile et par fois impossible à mesurer que la complexité des
processus à contrôler augmentent. D'une manière
radicalement opposée, un contrôleur va décrire non pas le
processus mais la façon de le contrôler, tout comme le ferait un
expert humain à travers des règles intégrant naturellement
imprécisions et incertitudes.
Quelques domaines d'application
La commande Floue :
Parmi les nombreuses applications de la logique floue, la
commande floue s'avère être le champ d'application le plus actif
à travers le monde.
Exemples :
· Commande de tubes broyeurs pour la fabrication du ciment
(première réalisation en 1979 au Danemark).
· Commande de métros avec un fonctionnement plus
confortable et économique et une précision d'arrêt
augmentée (1987 à Sendai, Japon).
· production du fer et de l'acier, purification, de
l'eau, chaînes et robots de fabrication,
· opérateurs, unités arithmétique,
micro-ordinateurs, ...
Classification et reconnaissance de
formes :
Classifier consiste à regrouper des objets en
catégories les plus homogènes possibles (contenant des objets
similaires) :
Classifier est une activité qui intervient dans des
nombreux domaines d'applications tels que :
· la reconnaissance vocale.
· L'analyse d'images (médical, radar,
télédétection).
· La reconnaissance de cibles (domaine militaire).
· consultation, investissement et développement,
horaires de train, ...
· base de données, recherche d'information,
modélisation de systèmes
Conception d'un régulateur à logique flou
Un contrôleur standard (PID ou autres) demande toujours un
modèle le plus précis possible (équations
différentielles).
Un contrôleur flou ne demande pas de modèle du
système à régler. Les algorithmes de réglage se
basent sur des règles linguistiques de la forme Si ... Alors ...
En fait, ces règles peuvent être exprimées en
utilisant le langage de tous les jours et la connaissance intuitive d'un
opérateur humain.
Ce qui conduit à deux avantages :
· Conclusion :
Pour les systèmes mal connus ou complexes
(non-linéaires), un contrôleur flou s'avère très
intéressant.
Structure du régulateur
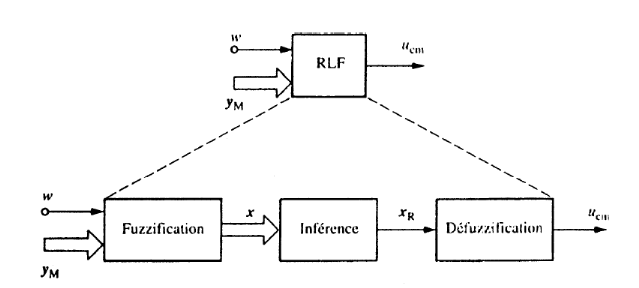
- Fuzzification : transforme les entrées en grandeurs
floues.
- Inférence (avec la base de règles) : prend
les décisions
- Défuzzification : transforme les grandeurs floues
en valeurs déterminées
Fuzzification
- Définition des fonctions d'appartenance de toutes les
variables d'entrée.
- Passage : grandeurs physiques => variables linguistiques
En général, on utilise des formes triangulaires ou
trapézoïdales pour les fonctions d'appartenance, bien qu'il
n'existe pas de règles précises sur ce choix.
Exemple : Soit une grandeur x définie par
5 sous-ensembles flous.
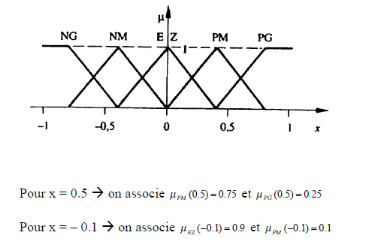
Donc à chaque variable linguistique d'entrée (x),
on fait correspondre une valeur linguistique (Négatif Grand,
Négatif Moyen, ...) avec un degré d'appartenance.
Inférence ou Base de règles
Donne la relation qu'il existe entre les variables
d'entrées (exprimées comme variables linguistiques) et la
variable de sortie (également exprimée comme variable
linguistique).
Exemple : Soit deux entrées x1 et x2 et une sortie xR,
toutes définies par les 5 sous-ensembles de l'exemple
précédent.
Description de la base de règles :
Si (x1 NG ET x2 EZ),
Alors xR PG ou
Si (x1 NG ET x2 PM),
Alors xR PM ou
Si (x1 NM ET x2 EZ),
Alors xR PM ou
Si (x1 NM ET x2 PM),
Alors xR EZ ou
Si (x1 NM ET x2 PG),
Alors xR NM ou
Si (x1 PG ET x2 EZ),
Alors xR NG.
Sous forme de tableau ou matrice :
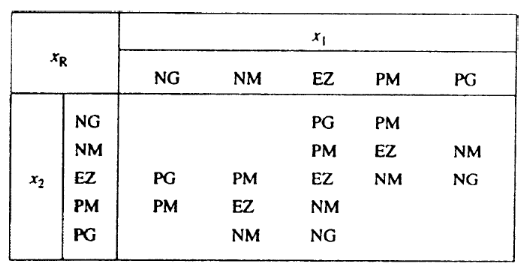
On n'est pas obligé de compléter toute la table.
Les règles sont élaborées par un expert et sa connaissance
du problème ...
Différentes méthodes d'inférence.
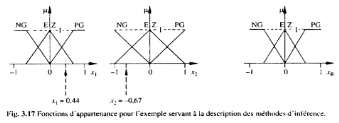
Supposons que l'on ait deux entrées x1 et x2 et une sortie
xR, toutes définies par les sous-ensembles suivants :
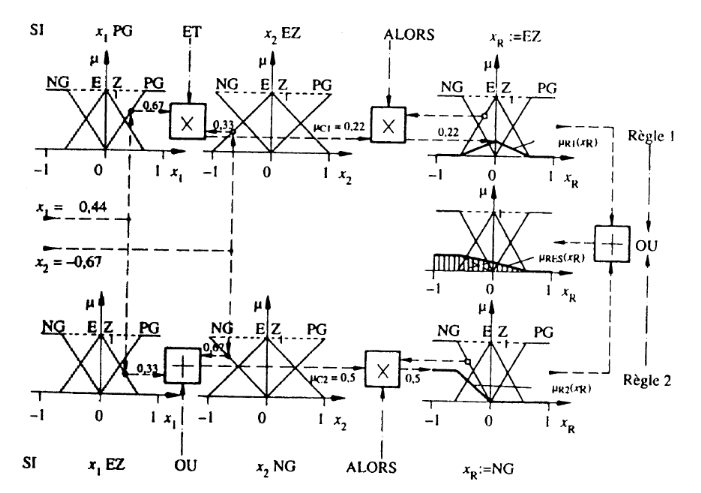
Supposons que x1 = 0.44, x2 = - 0.67 et que l'inférence
est composée des deux règles suivantes :
Si (x1 PG ET x2 EZ),
Alors xR EZ ou
Si (x1 NG OU x2 PM),
Alors xR PM
Il faut maintenant « traduire » les opérateurs
ET, OU et l'implication par une des fonctions vues dans la première
partie de l'exposé
(Minimum, Maximum, Produit, ...).
Méthode MAX-MIN :
Au niveau de la condition : ET => Min OU => Max
Au niveau de la conclusion : ou => Max Alors => Min
(D'où la désignation)
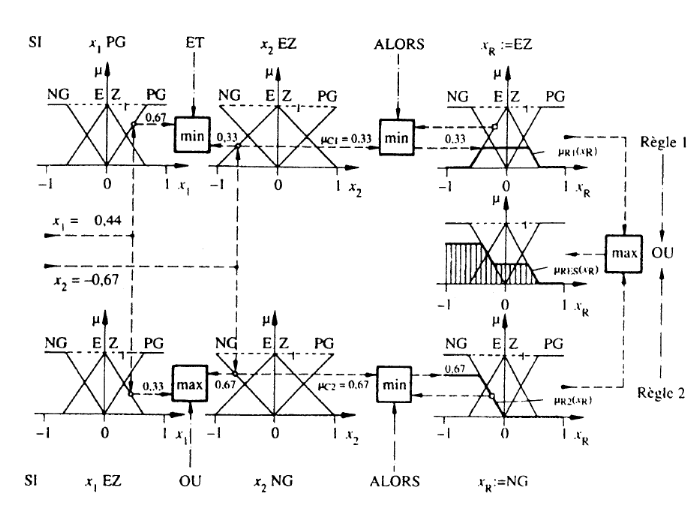
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Méthode MAX-PROD :
Au niveau de la condition : ET => Min OU => Max
Au niveau de la conclusion : ou => Max Alors => Prod
(D'où la désignation)
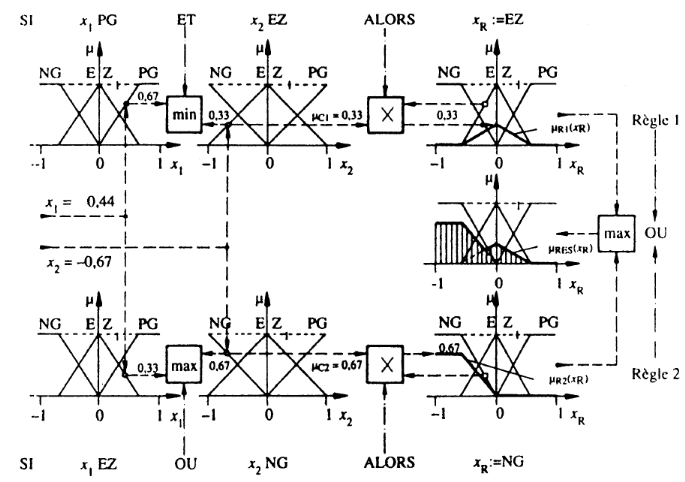
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Méthode SOMME-PROD :
Il ne s'agit pas de la Somme « normale » mais de la
valeur moyenne :
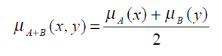
Au niveau de la condition : ET => Prod OU => Somme
Au niveau de la conclusion : ou => Somme Alors => Prod
(D'où la désignation)
Résultat : une fonction de transfère
résultante donnée par la surface hachurée (qui sera
traitée lors de la Défuzzification).
Défuzzification
Les méthodes d'inférence fournissent une fonction
d'appartenance résultante pour la variable de sortie. Il s'agit donc
d'une information floue qu'il faut transformer en grandeur physique.
On distingue 4 méthodes de Défuzzification :
Méthode du maximum :
La sortie correspond à l'abscisse du maximum de la
fonction d'appartenance résultante.
Trois cas peuvent se produire :
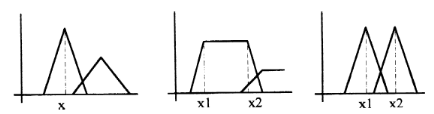
Conclusion : méthode simple, rapide et facile mais elle
introduit des ambiguïtés et une discontinuité de la
sortie.
Méthode de la moyenne des maxima :
Dans le cas où plusieurs sous-ensembles auraient la
même hauteur maximale, on réalise leur moyenne une des
ambiguïtés de la méthode du maximum est enlevée.
Méthode du centroïde :
La sortie correspond à l'abscisse du centre de
gravité de la surface de la fonction d'appartenance
résultante.
Il existe deux méthodes :
- On prend l'union des sous-ensembles flous de sortie et on en
tire le centroïde global (calculs très lourds).
- On prend chaque sous-ensemble séparément et on
calcul son centroïde, puis on réalise la moyenne de tous les
centroïdes.
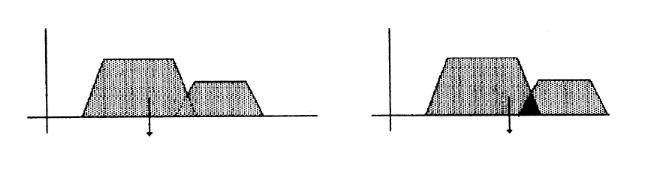
Conclusion : on n'a plus de discontinuités et
d'ambiguïtés, mais cette méthode est plus complexe et
demande des calculs plus importants.
Méthode de la somme pondérée
:
Compromis entre les deux méthodes
précédentes.
On calcule individuellement les sorties relatives à
chaque règle selon le principe de la moyenne des maxima, puis on
réalise leur moyenne pondérée.
| 


