IV.2.3 Bloc de découplage
En reprenant la description de la commande vectorielle par
orientation du flux rotorique sur l'axe (d) du repère lié au
champ tournant et en réécrivant le système
d'équation (IV.2) de la manière suivante :
|
ids = *
|
Ö*
r
1 d *
+ Ö
( T )
r r
M dt
|
*

iqs = *
L C
r em (IV.3)
pM Ö * r
*
ù =
sg
ÖT r r
*
i
M
qs

*
Ö *
r
Cem*


Lr
p M
.

M

Tr


÷
÷
Figure (IV.3) : Structure de commande par flux orienté
(CFO)
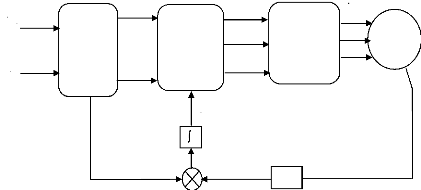
La figure (IV. 4) donne le schéma bloc de
découplage par orientation du flux rotorique. Nous réalisons la
commande découplée suivante :
*
Ö
r
+ ùr
?
ibs
ias
ics
*
*
*
Onduleur de tension commandé en courant
ias
ibs
ics
MAS
ids
*
CFO
P-1 (ès *)
ès*
P
Cem *
ùsg* +
Figure (IV.4): Schéma de découplage par orientation
du flux rotorique
IV.3 Réglage de la vitesse par la méthode
indirecte
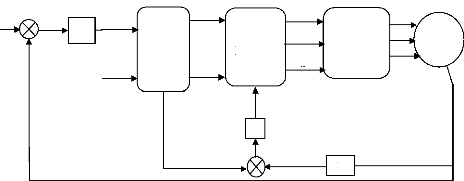
Concernant le réglage de vitesse, celui-ci est
donné par le schéma fonctionnel de régulation de la figure
(IV.5). Un régulateur de type PI a été rajouté au
montage de découplage de la figure (IV.4)
?*
+
-
PT
Cem *
Ö
*
r
CFO
ùsg *
Tqs *
Tds *
+
P-1 (ès*)
?
ès*
+
ùs *
ias *
ibs *
ics *
ùr
Onduleur de tension à hystérésis
P
?
ics
ibs
ias
MAS
Figure (TV.5): Schéma fonctionnel de régulation
de vitesse d'une machine
asynchrone commandée par la technique du
flux oriente (méthode indirecte)
IV.3.1 Synthèse du régulateur PI
Le régulateur de vitesse permet de déterminer le
couple de référence, afin de maintenir la vitesse de
référence correspondante.
L'équation mécanique donne:
? ( ) 1
s
C s f Js
em ( ) +
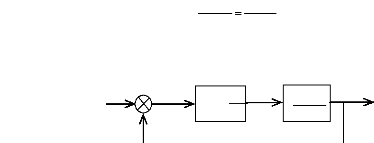
En associant à cette fonction un régulateur PT, il
arrive:
e? (s)
-
Cem(s)
?
s
1
f + Js
?*
k p
? +
k i
?(s)
(TV.4)
Figure (TV.6): Schéma fonctionnel de régulation de
vitesse.
La fonction de transfert en boucle fermée, calculée
à partir du schéma précédent, est donnée
par:
(k p s k i ? + ? )
? ( )
s
1
J
(TV.5)
( )
s P s
( )
? *
L'équation caractéristique P(s) est:
f k
+ k
2 p ? i ?
P s s
( ) = + s + = (TV.6)
0
J J
En imposant toujours deux pôles complexes conjugués
s1 ,2 = ñ (-1 #177; j) , en boule fermée et,
par identification avec la nouvelle équation caractéristique
désirée, on arrive à:
k ? J ñ et k p
2
i 2
= ? = 2ñJ f
- (IV.7)
IV.4 Résultats de la simulation
Dans le but de valider l'influence des défauts
rotoriques sur le modèle réduit du schéma multi -
enroulement de la machine asynchrone a cage d'écureuil, nous avons
simulé ce schéma en commande indirecte de vitesse. Les
performances de la commande ont été évaluées pour
une machine saine ainsi en présence de défauts rotoriques
(ruptures de barres), pour une inversion du sens de rotation avec et sans
variations du couple de charge.
IV.4.1 Cas d'une machine saine
a- Machine saine à vide
Les paramètres du régulateur de vitesse
utilisé dans l'ensemble des simulations qui serons
présentées par la suite, sont calculés pour ñ=100.
L'algorithme de simulation est réalisé avec une période
d'échantillonnage de 0.5ms.
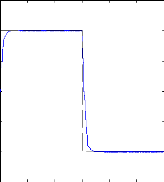
La figure (IV.7) représente les réponses de la
vitesse de rotation (n) et du couple électromagnétique
Cem, à une inversion du sens de rotation de 1000 tr/mn
à -1000 tr/mn. En absence d'un couple de charge, le couple se stabilise,
après un régime transitoire, à une faible valeur qui
compense les frottements.
Dans la simulation de la figure (IV.5) nous avons introduit un
filtre pour la référence dans le but de modérer l'impact
de sa variation brusque sur la réponse en vitesse de la machine ce qui
amorti la rapidité du réglage et limite le dépassement.
La fonction de transfert à prévoir dans notre cas
est donnée par :
( )
? * filtrée 1
= (IV.8)
? * (1 )
+ Tf S
La constante du temps Tf est calculée de façon
à compenser le zéro de la fonction de transfert par
rapport à la consigne donnée par l'équation
(IV.5). Donc p
T k
=
f
, des simulations ont montré
k
?
i ?
qu'il est judicieux de travailler avec une valeur de Tf trois
fois la valeur prévue, afin d'avoir des réponses de faibles
dépassements.
La figure (IV.9) illustre l'évolution temporelle, en
régime transitoire et en régime permanent, des courants de barres
rotoriques irb0 , irb1, irb2, irb3. Après le démarrage et en
absence d'un couple de charge, ces courants se stabilisent à des valeurs
proche de zéro.
II (trim n )
-1000
-1500
1500
1000
-500
500
0
0 0.5 1 1.5 2 2.5 3
-80
0 0.5 1 1.5 2 2.5 3
t(s )t(s)
a
C em (11 .m
-20
-40
-60
60
40
20
0
b
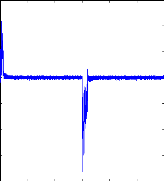
Figure (IV.7) : Réponses de la machine asynchrone saine
lors d'une inversion du sens
de rotation : a) vitesse de rotation et sa
référence , b) couple électromagnétique.
40
30
zoom
20
-10
-20
-30
0 0.5 1 1.5 2 2.5 3
t(s )
10
0
ias(A )
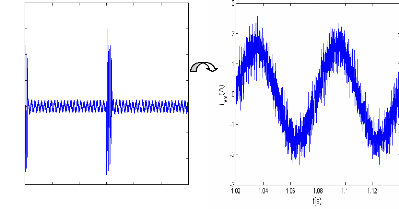
Figure (IV.8) : Courant de phase statorique.
2000
1500
1000
-1000
-1500
-200 0
0 0.5 1 1.5 2 2.5 3
t(s ) t(s )
0 0.5 1 1.5 2 2.5 3
2000
1500
1000
500
0
irb0(A
-500
-1000
-1500
-200 0
500
0
irb (A )
-500
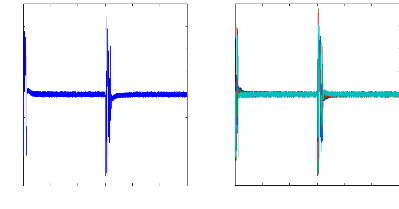
Figure (IV.9) : courants dans les barres rotoriques,
Irb0 , Irb1 , Irb2 , Irb3, simulation avec
modèle global, machine saine à vide
ids(A)
1 5
1 0
-5
5
0
0 0 .5 1 1 .5
t(s )
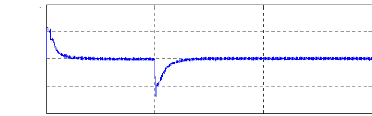
iqs(A)
-2 0
-4 0
4 0
2 0
0
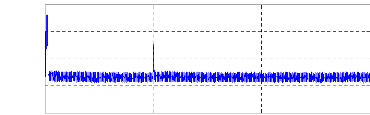
0 0 .5 t(s ) 1 1 .5 Figure
(IV.10) : Découplage par orientation du flux rotorique.
b- Cas d'une machine saine en charge
Pour illustrer les performances du réglage, nous avons
simulé un démarrage à vide avec une application du couple
de charge (Cr=3.5Nm) à l'instants t = 0.5s, suivi d'une
inversion de la référence de vitesse entre #177;1000 tr/mn
à l'instant t=1.5s.
Les résultats obtenus sont regroupés sur les
figures (IV.11-12). Comme on peut le constater, ces
résultats
montrent que la commande vectorielle appliquée à la machine
asynchrone permet un
rejet de la perturbation et une bonne poursuite de la
référence. Toutefois, un pic de couple de
valeur importante apparaît lors de l'inversion de la
vitesse ce qui est néfaste pour le bon fonctionnement de la machine.
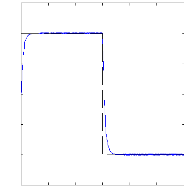
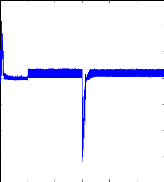
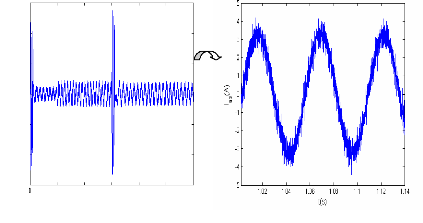
La figure (IV.13) présente les courants des quatre
premières barres rotoriques. En présence d'un couple de charge,
les courants rotoriques deviennent des ondes sinusoidales.
II (trim n )
-1000
-1500
1500
1000
-500
500
0
a
-
C en (11 .m )
-40
-60
-80
60
40
20
0
0
b
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
30
-10
-20
-30
0.5 1 1.5 2 2.5 3
t(s)
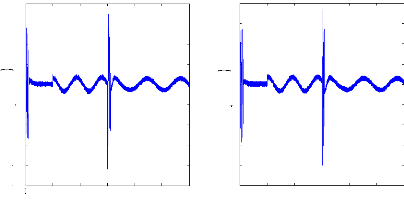
Figure (IV.12) : Courant de phase statorique d'une machine
asynchrone saine en charge.
zoom
0
ias(A )
20
10
Figure (IV.11) : Réponses de la machine asynchrone saine
en charge lors d'une inversion du sens
de rotation : a) vitesse de rotation
et sa référence , b) couple électromagnétique.
2000
1500
1000
500
0
00
-1000
-1500
-2000
-2500
0 0.5 1 1.5 2 2.5 3
t (s t (s
611A
-5
0.5 1 1.5 2 2.5 3
2000
1500
1000
500
0
irbo (A
-
500
-1000
-1500
2000
2500
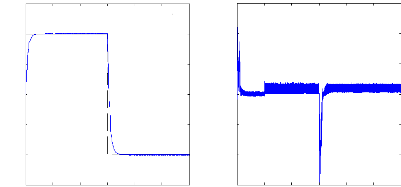
Figure (IV.13) : courant dans la barre rotorique : Irb0 ,
Irb1
simulation avec modèle global, machine saine en charge,
Cr= 3.5 N.m
IV.4.2 Cas d'une machine avec défaut
On va voir la régulation de la vitesse, dans le cas des
défauts, ou on simule la rupture d'une barre, et aussi la rupture de
deux barres.
a- Cas d'une rupture d'une barre
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
Cem(N.m)
-20
-40
-60
60
40
20
0
b
II (trim n)
-1000
-1500
1500
1000
-500
500
0
a
Figure (IV.14) : Réponses de la machine asynchrone en
charge avec un défaut lors d'une
inversion du sens de rotation : a)
vitesse de rotation et sa référence , b)
couple
électromagnétique.
t(s )
t(s )
1500
1000
500
0
irboIA
-500
-1000
-1500
Figure (IV.15) : Courant de phase statorique, machine en
défaut, en charge Cr= 3.5Nm
0 0.5 1
t(s )1.5 2 2.5 3
0 0.5 1 1.5 2 2.5 3
t(s )
30
20
10
0
ias(A )
-10
-20
-30
0 0.5 1 1.5 2 2.5 3
1 1.05 1.1 1.15 1.2 1.25 1.3
5
4
zoom
3
2
0
ias(A )
-1
-2
-3
-4
-5
3000
2000
00
0
-1000
irb 0 ,1 ,2 ,3 (A--)
10
-2000
-3000
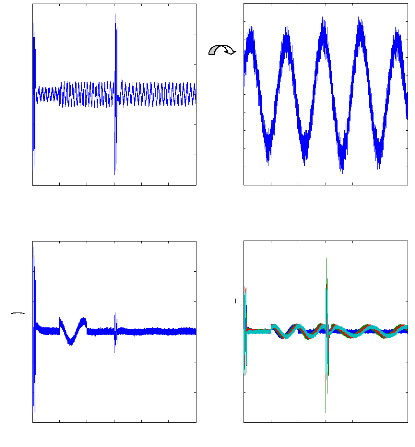
Figure (IV.16) : Courants dans les barres rotoriques : Irb0 ,
Irb1 , Irb2 , Irb3 machine en défaut,
simulation avec modèle global, rupture de la barre rb0
à t= 1s
b- Cas d'une rupture de deux barres
II (trim n )
-1000
-1500
1500
1000
-500
500
0
a
0 0.5 1 1.5 2 2.5 3
t(s )
C em (11 .m )
-20
-40
-60
60
40
20
0
b
0 0.5 1 1.5 2 2.5 3
t(s)
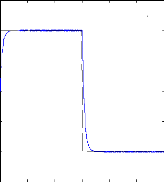
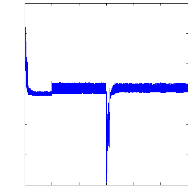
Figure (IV.17) : Réponses de la machine asynchrone en
charge avec un défaut lors d'une
inversion du sens de rotation : a)
vitesse de rotation et sa référence , b)
couple
électromagnétique
0 0.5 1 1.5 2 2.5 3
t(s)
1 1.05 1.1 1.15 1.2 1.25 1.3
t(s )
ias(A )
-10
-20
-30
30
20
10
0
-1
-2
-3
-4
-5
5
4
3
2
0
1
zoom
ias(A )
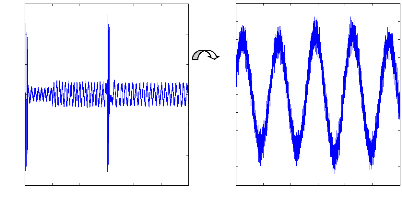
Figure (IV.18) : Courant de phase statorique, machine en charge
et en défauts, 2 barres cassées
0 0 .5 1 1 .5 2 2 .5 3
t(s )
irb1(A
-1 0 0 0
-2 0 0 0
-3 0 0 0
3 0 0 0
2 0 0 0
1 0 0 0
0
1 0 0
irb0,1,2,3(A--)
-1000
-200 0
-3000
3 0 0 0
2 0 0 0
0
0
0 0.5 1 1.5 2 2.5 3
t(s)
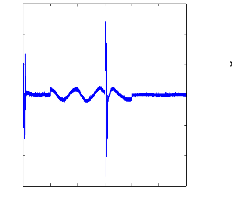
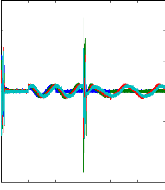
Figure (IV.19) : courants dans les barres rotoriques : Irb0 ,
Irb1 , Irb2 , Irb3
Machine en charge et en
défaut, simulation avec modèle global : 1 barre cassée
rb0 à t=1s, 2
barre cassée rb1 à
t=2s
Nous avons simulé dans la figure (IV.17) une inversion du
sens de rotation de +1000 tr/mn à -1000 tr/mn. Ce changement du sens de
rotation se déroule à couple maximal et le temps d'inversion en
charge est de l'ordre de 0.3 s.
La figure (IV.17) représente l'évolution du couple
et la vitesse, quand la référence de vitesse est un
échelon d'amplitude 1000 tr/mn. Le temps de réponse de la vitesse
est de l'ordre de 0.2 s, Un échelon de couple de 3.5 N.m est
appliqué à t=0.4s. Le régime ainsi établi, nous
procédons à la simulation d'une première rupture de barre
par une augmentation de 11 fois la résistance de cette barre.
Après un régime transitoire très bref, la deuxième
barre est cassée à t=2s.La vitesse reste toujours peu
perturbée par ce défaut.
Le régulateur de vitesse adopté doit avoir un
comportement satisfaisant sur toute la plage de vitesse de 0 à 1000
tr/mn et doit satisfaire le plus possible aux exigences suivantes
- rapidité de réponse
- dépassement nul ou faible (< 10%)
- erreur statique nulle en régime permanent
- robustesse aux variations paramétriques
Dans la figure (IV.18), nous observons une déformation au
niveau du courant statorique , lors des cassures de barres.
La figure (IV.19) montre les courants dans les barres rotoriques
Irb0 , Irb1 , Irb2 , Irb3 , ou on
voit que irb0 s'annule a cause de la cassure de barre rb0
à t=1s, et pour rb1 à t=2s, pour irb2
et irb3, on remarque une déformation dans les allures.
| 


