Chapitre III
Modélisation et simulation des
défauts
rotoriques de la machine asynchrone
III.1 Introduction
La méthode qu'on a adoptée pour la simulation
des défauts rotoriques consiste à remplacer la valeur initiale de
la résistance des barres cassées par une valeur finie. Cette
méthode est appelée méthode des résistances
finies.
E. Ritchie estime qu'une augmentation de la résistance de
la barre de 11 fois permet d'aboutir à des résultats en
concordance avec ceux obtenus expérimentalement.
En ce qui nous concerne nous avons considéré des
augmentations de 11 fois la résistance initiale de la barre.
En effet pour un pas de 3
10- s, une augmentation de plus de 11 fois conduit
à une instabilité numérique (dans notre modèle).
La méthode d'intégration est celle de Runge Kutta
d'ordre 4.
III.2 Modélisation des défauts dans le cas
de cassures d'une et de deux barres
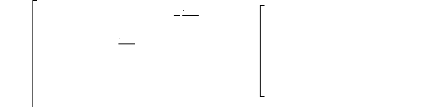
Le modèle II.39 démontré dans le chapitre
précédent, et réécrit ci-dessous, permet de simuler
la rupture de barres au rotor.
-
2
3 Msr
Lsc
0
0
0 0
2
3 Msr
Lsc
0
0 Lrc 0
0
Nr
2

0
0 0
Msr

Nr
2
0 0
Msr
0 Ò
0 L rc 0

dt
d
i ds
i qs
i dr
i qr
Ie
1
? ? ? ? ?
? ?
1 ?
?
?
?
?
?
?
? ?
ids
i qs
i dr
(III.1)
i qr
Ie
1 ? ? ? ? ?
? ?
Nr
ùM
0
sr
2
-
Nr
ùM
0 0
ùL R
sr
sc
2
-
0
Re
0 0 0
R s - ùL 0
sc
0 0 S 1 S 2 0
0 0 S 3 S 4 0
1 ? ? ? ? ?
? ?
Vds
Vqs
0
0
0
Avec:
|
S 1 = 12 6 [(2 NR e r + R b 0 +
Rb15 )cos2 0
a + (2 N Re r +
Rb1 +Rb0 )cos2 la
+
·
·
· + (2 NRe r +
R b15 Rb
)coS2
|
? ()?
15á
?
|
1 rf \\ \\
- RR b° cos0á
) cosOá p+ ( Rb1
cos0á ) coR2á p+
·
· +
(R615(R615cos0
5á ) coR \\-1 0a (III.2)
4 6
i
i
S2 = - 2 6 [(2 R e r +
A0 +g15 jcos0 ásin0 á
-(2 R e r +R +g0 jcos1 á
sin1 á (2 R e + A15
+Rbdcos1 5ásin1
N Nr
+ 2 6 [ ( R b 0 sin( 0á ) cos(
1á)) + ( Rb1 sin( 1 á
) cos( 2á)) +
·
·
· + (
Rb15 sin( 1 5á ) cos(
0á ))]
+ 6 [(R b° cos(
0á ) sin( 1á)) + (
Rb1 cos( 1á ) sin(
2á))+
·
·
· + (
Rb15 cos( 1 5á ) sin(
0á ))] (III.3)
1
i
i
2 R e Re
S
3 = - 42 Re + A0 +k5 jcos0
á sin0 á -(2 +R +R
}oslá sinlá - -
·
'-(2 + Rb15 +
k4 jcos1 5ásin1
Nr
r r
+ 2 6 [(R b 0 sin( 0á ) cos(
1á)) + ( Rb1 sin( 1 á
) cos( 2á)) +
·
·
· + (
Rb15 sin( 1 5á ) cos(
0á ))]
+ 6 [(R b° cos(
0á ) sin( 1á)) + (
Rb1 cos( 1á ) sin(
2á))+
·
·
· + (
Rb15 cos( 1 5á ) sin(
0á ))] (III.4)
1
|
S = 12 6 ft R r bo
bo) ( R r ) ( R r )
2 e + R + R
cos2 0 á + 2 e +
RbI + Rb0
cos2 1á +
·
·
· + 2
e + R A1 5 + R cos2
15á
4 4," b14
|
1 1
i
|
4 rf , \ , \\ , , \ , \\ , ,
\cos(0a ))] (III.5)
- RR cos0á )cosOáD+
Ob1 cos0á
)coR2áp+
·
·
· + Ob15
cos(15a)cos(0a 5a ) 1 6 b 0
Dans le cas oil on veut simuler la rupture d'une barre ou de deux
barres les seules valeurs qui vont changer sont celles de: S1, S2, S3 et S4
III.2.1. Cassures de barres
La cassure de barres est un des defauts les plus frequents au
rotor. Nos simulations nous permettrons d'identifier les signatures de ce
defaut et de prevoir les deteriorations generees dans le moteur.
Pour illustrer la cassure totale de barre dans le modèle
de la machine, nous augmentons la valeur de la barre cassee de 11 fois [7].
III.2.2 Simulation des défauts rotoriques
à vide et en présence d'une charge sur l'arbre du
moteur
III.2.2.1 Machine à vide
a. Cas d'une cassure d'une barre
. Alimentation sans onduleur
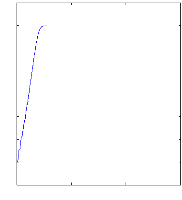
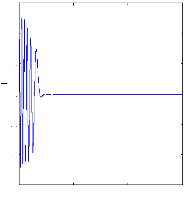
On n'impose tout d'abord aucun couple de charge. La figure III.1
illustre l'evolution temporelle
en regime transitoire et en regime permanent de la vitesse de
rotation en presence d'une rupture de barre (rb0) a t=1s, Apres une
phase transitoire, celle-ci se stabilise a une valeur proche de la vitesse de
synchronisme a cause de l'absence d'un couple de charge. La figure illustre
aussi l'evolution temporelle en regime transitoire et en regime permanent du
couple electromagnetique
Cem en présence d'une rupture de barre (rb0). Après
une phase transitoire, celui-ci se stabilise a une valeur proche de zéro
a cause de l'absence d'un couple de charge.
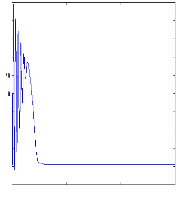
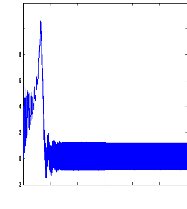
La figure III.2 illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique ,
en présence d'une rupture d'une barre (rb0) à t=1s
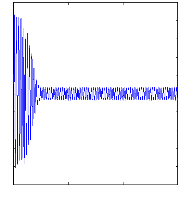
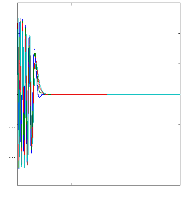
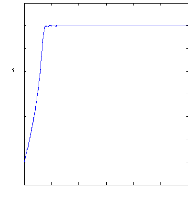
La figure III.3 illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1 , Irb2 , Irb3 , en présence d'une
rupture des barres (rb0) à t=1s .
On remarque dans l'essai à vide, les signatures des
défauts rotoriques sont très minimes.
3500
3000
2500
2000
500
1
n(trLm n)
1000
500
0
-500
0 0.5 t(s) 1 1.5
0 0.5 1 1.5
t(s)
1
Cem (N.rn)
18
16
14
12
-2
6
4
2
0
0 0.5 1 1.5
t(s)
ia s (A )
-10
-15
-20
-25
25
20
15
10
-5
5
0
Figure III.1 : vitesse de rotation, couple
électromagnétique ( simulation avec le
modèle
réduit, machine en défaut à vide)
0 0 .5 1 1 .5
t(s)
irb 0 (A
· 1 0 0 0
· 1 5 0 0
1 5 0 0
1 0 0 0
· 5 0 0
5 0 0
0
0 0.5 1 1.5
t(s)
irb (A
· 1000
· 1500
1500
1000
· 500
500
0
0 0.5 1 1.5 2 2.5 3
t(s)
1
1
k(trim n )
3 5 0 0
3 0 0 0
2 5 0 0
· 500
0 0 0
5 0 0
0 0 0
500
0
0 0.5 1 1.5 2 2.5 3
t(s)
Cem(N.m
12
10
·
Figure III.3 :courants dans les barres rotoriques,
Irb0,Irb1,Irb2,Irb3,
simulation avec modèle global, machine en
défaut à vide.
. Alimentation avec onduleur
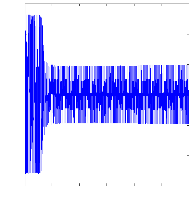
0 0.5 1 1.5 2 2.5 3
t(s)
ias(A )
-10
-15
15
10
-5
5
0
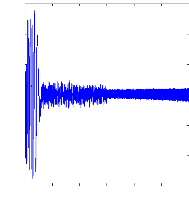
0 0.5 1 1.5 2 2.5 3
t(s)
irbO(A )
-1000
-1500
1500
1000
-500
500
0
Figure III.4 : Simulation avec le modèle réduit,
machine en défaut à vide, alimentation avec
onduleur
b- Cas d'une cassure de deux barres
. Alimentation sans onduleur
La figure III.5 illustre l'évolution temporelle en
régime transitoire et en régime permanent de la vitesse de
rotation en présence d'une rupture de deux barres (rb0)
à t=1s et (rb1) à t=2s, Aprés une phase
transitoire, celle-ci se stabilise à une valeur proche de la vitesse de
synchronisme à cause de l'absence d'un couple de charge. La figure
illustre aussi l'évolution temporelle en régime transitoire et en
régime permanent du couple électromagnétique
Cem en présence d'une rupture des barres (rb0)
à t=1s et (rb1) à t=2s. Après une phase
transitoire, celui-ci se stabilise à une valeur proche de zéro
à cause de l'absence d'un couple de charge. La figure III.6 illustre
l'évolution temporelle en régime transitoire et en régime
permanent du courant statorique , en présence d'une rupture d'une barre
(rb0) à t=1s et (rb1) à t=2s.
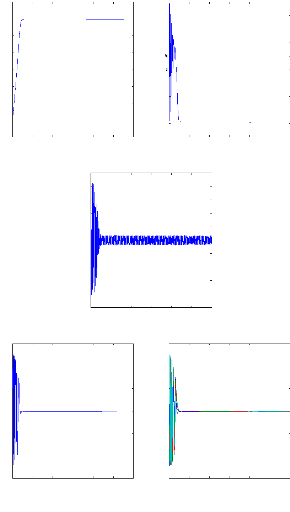
La figure III.7 illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1 , Irb2 , Irb3 , en
présence d'une rupture des barres (rb0) à t=1s et
(rb1) à t=2s.
500
0
irb 0 (A )
-500
2 2.5 3
0 0.5 1 1.5
3500
3000
2500
2000
500
1
n(trLm n )
1000
500
0
-500
18
16
14
12
6
1
Cem (N.rn)
4
2
0
-2
0 0.5 1 1.5 2 2.5 3
0 0.5 1 1.5 2 2.5 3
)
Figure III.5 : vitesse de rotation, couple
électromagnétique ,
t(s )
t(s
simulation avec le modèle réduit, machine en
défaut à vide
0 0.5 1 1.5 2 2.5 3
ia s (A )
-10
-15
-20
-25
25
20
15
10
-5
5
0
t(s)
Figure III.6 : courant statorique, simulation avec
le
modèle réduit, machine en défaut à vide
t(s)
0 0.5 1 t(s) 1.5 2 2.5 3
irb (A )
-1000
-1500
1500
1000
-500
500
0
1500
1000
-1000
-1500
Figure III.7 :courants dans les barres rotoriques Irb0 , Irb1 ,
Irb2 , Irb3,
simulation avec modèle global, machine en
défaut à vide
2. Alimentation avec onduleur
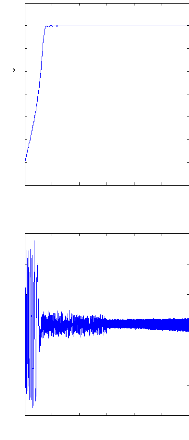
1500
1000
500
0
irbo IA I
-500
-1000
-1500
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s )
k(trim n )
1
1
3500
3000
2500
-500
000
500
000
500
0
15
10
5
0
ia s (A )
-5
-10
-15
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
Cem(N.m
12
10
-2
8
6
4
2
0
Figure III.8 : Simulation avec le modèle réduit,
machine en défaut à vide, alimentation avec
onduleur
2. Machine en charge
a. Cas d'une cassure d'une barre 2. Alimentation sans
onduleur
On impose maintenant un couple de charge de 3.5 N.m à
t=0.6s et la machine opère alors en charge.
La figure III.9 illustre l'évolution temporelle en
régime transitoire et en régime permanent de la vitesse de
rotation, celle-ci se stabilise a une valeur de 2219 tr/mn. La figure illustre
aussi du couple électromagnétique Cem en présence d'une
rupture des barres rb0 à t=1s. Aprés une phase
transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de
la présence du couple de charge.
La figure III.10 illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique ,
en présence d'une rupture de barre rb0 à t=1s .
La figure III.11 illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1 , Irb2 , Irb3, en
présence d'une rupture de barre rb1 à t=1s. Les
courants circulant dans les barres adjacentes aux barres cassées sont
très supérieurs a leur valeur nominale. On conclut donc qu'il y a
un risque de défaillances en chacune dans la mesure ou les contraintes
électriques et thermiques sont redistribuées sur les conducteurs
adjacents.
Nous observons se qui suit:
- La vitesse chute à 2917 tr/mn, et le couple
électromagnétique vient équilibrer le couple
résistant .
- La détérioration de la barre réduit la
valeur moyenne du couple électromagnétique et fait
apparaître les oscillations .
- L'oscillation sur la vitesse .
- Les courants des phases statoriques sont toujours
déphasés entre eux de 120°,
Cependant une ondulation de l'amplitude des courants
apparaît avec la cassure de la barre, la figure III.9 illustre cette
ondulation.
- Le rotor avec ce défaut de la structure crée
en plus de champ rotorique direct qui tourne à g*ùs par rapport
au rotor , un champ inverse qui lui tourne à -g*ùs dans le
repère rotorique. L'interaction de ces champs avec celui issu du
bobinage statorique donne naissance à un couple
électromagnétique (somme d'une composante directe constante et
d'une composante inverse sinusoïdale), de pulsation 2g ùs
.Elle sera la cause d'oscillations sur la vitesse [3].
18
16
14
12
10
8
6
Cem(N.m
4
2
0
-2
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
3 5 0 0
3 0 0 0
2 5 0 0
0 0 0
5 0 0
0 0 0
1
1
k(trim n )
500
0
-500
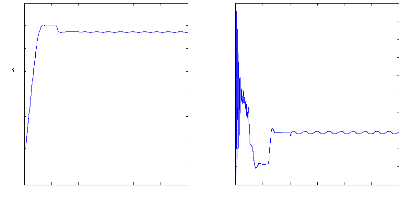
Figure III.9 : vitesse de rotation, couple
électromagnétique et le courant statorique, simulation
avec le
modèle réduit, machine en défaut en charge,
Cr=3.5 N.m
0 0.5 1 1.5 2 2.5 3
ia s(A )
-10
-15
-20
-25
25
20
15
10
-5
5
0
t(s)
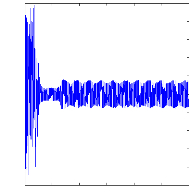
Figure III.10 : courant statorique, simulation avec le
modèle réduit, machine avec défaut
en
charge,Cr=3.5 N.m
0 0.5 1 1.5 2 2.5 3
t(s)
0
irb o(A )
-1000
-1500
-2000
1500
1000
500
-500
2000
0 0.5 1 1.5 2 2.5 3
t(s)
irb (A )
-1000
-1500
-2000
2000
1500
1000
-500
500
0
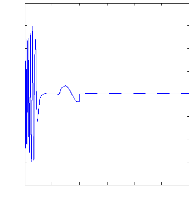
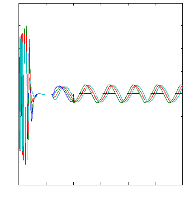
Figure III.11 :courants dans les barres rotoriques Irb0 , Irb1
, Irb2 , Irb3,
simulation avec modèle global, machine en
défaut en charge, Cr=3.5N.m
2. Alimentation avec onduleur
12
10
8
6
4
Cem(N.m)
2
0
-2
15
10
5
ia s(A )
-5
-10
-15
1500
1000
500
0
irb o IA )
-500
-1000
-1500
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
3500
3000
2500
000
500
000
k(trim n )
1
1
500
0
-500
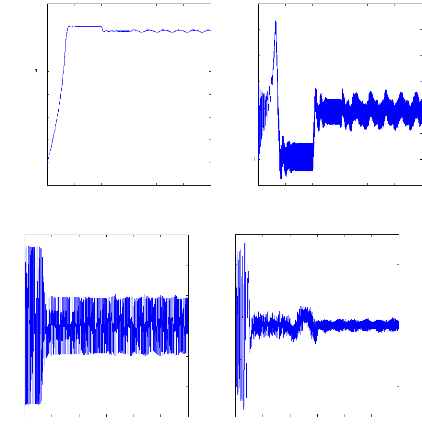
Figure III.12 : Simulation avec le modèle réduit,
machine en défaut en charge , alimentation avec
onduleur
a- Cas d'une cassure de deux barres
1. Alimentation sans onduleur
On impose maintenant un couple de charge de 3.5 N.m à
t=0.6s et la machine opère alors en charge.
La figure III.13 illustre l'évolution temporelle en
régime transitoire et en régime permanent du couple
électromagnétique Cem en présence d'une rupture
de barre rb0 a t=1s et rb1 a t=2s. Aprés une phase transitoire, celui-ci
se stabilise a une valeur proche de 3.5 N. m a cause de la présence du
couple de charge. On constate des oscillations du couple
électromagnétique a la fréquence 2gfs0 en régime
permanent.
La figure III.14 illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique,
en présence d'une rupture de barre rb0 à t=1s et
rb1 a t=2s.
La figure III.1 5 illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1 , Irb2 , Irb3 en
présence d'une rupture de barre rb1 à t=1 s. Les
courants circulant dans les barres adjacentes aux ban-es cassées sont
très supérieurs a leur valeur nominale. On conclut donc qu'il y a
un risque de défaillances en chacune dans la mesure ou les contraintes
électriques et thermiques sont redistribuées sur les conducteurs
adjacents.
Les effets de la cassure de barre (oscillation de ù et
Cem) croit rapidement avec le nombre de ban-es cassé ;
d'où on observe:
- Augmentation de l'amplitude des oscillations. La grande
amplitude des oscillations accélère la
détérioration de la machine.
- L'amplitude des courants des phases statoriques. est
proportionnelle au nombre de barres cassées.
- Lors des défauts rotoriques, les courants dans les
barres cassées chutent pratiquement zéro, tandis que les courants
dans les barres voisines deviennent déséquilibrés. Les
courants qui conduisaient les barres cassées se répartit alors
dans les barres voisines
18
16
14
12
10
8
6
C em (11 .m )
4
2
0
-2
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
3500
3000
2500
000
500
000
II (trim II)
1
1
500
0
-500
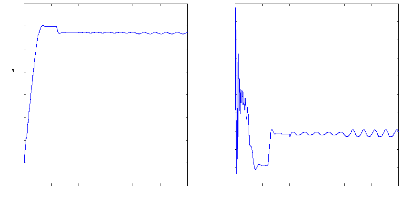
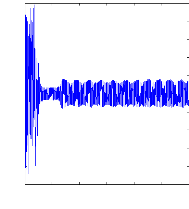
Figure III.13 : vitesse de rotation, couple
électromagnétique, simulation avec le
0 0.5 1 1.5 2 2.5 3
t(s )
ias(A )
-10
-15
-20
-25
25
20
15
10
-5
5
0
modèle réduit, machine en défaut en charge,
Cr=3.5 N.m
Figure III.14 : courant statorique, simulation avec le
modèle réduit, machine avec défaut
en
charge,Cr=3.54N.m
2000
1500
1000
500
0
irb (A )
-500
-1000
-1500
-2000
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
t(s )
2000
1500
1000
500
-500
0
!rbotA
-1000
-1500
2000
Figure III.15 :courants dans les barres rotoriques Irb0 , Irb1 ,
Irb2 , Irb3 simulation avec modèle global, machine en défaut en
charge, Cr=3.5N.m
12
10
8
6
4
Cem(N.m )
2
0
-2
0 0.5 1 1.5 2 2.5 3
t(s )
0 0.5 1 1.5 2 2.5 3
1
t(s )
3500
3000
2500
000
500
(trim n )
1
000
500
0
-500
2. Alimentation avec onduleur
15
10
5
0
ias(A )
-5
-10
-15
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
irb1(A)
-1000
-1500
1500
1000
-500
500
0
1500
1000
500
0
irboIA )
-500
-1000
-1500
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
irb3(A
-1000
-1500
1500
1000
-500
500
0
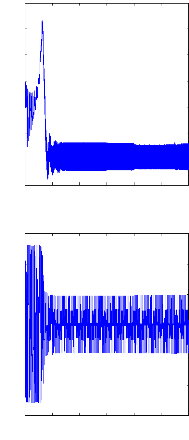
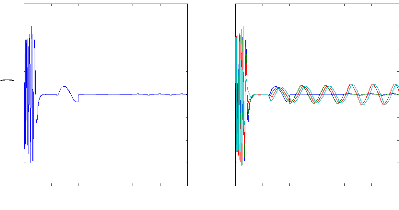
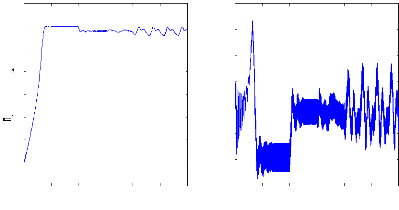
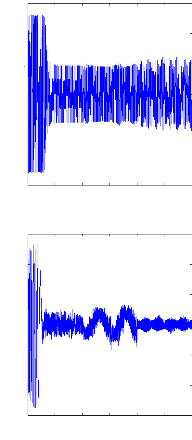
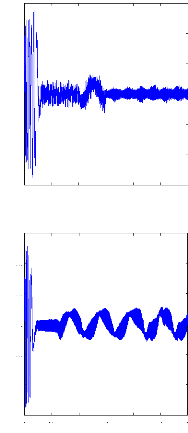
Figure III.16 : Simulation avec le modèle réduit,
machine en défaut et en charge ,
alimentation avec onduleur
III.3. Analyse spectrale de la signature du courant en
présence des défauts rotoriques [2]
[3]
Lors de la rupture de barre, il est difficile d'analyser
directement le courant statorique. Ce dernier ne présente en effet
qu'une petite modulation (figure III.3).
L'analyse par FFT permet de mettre en évidence les raies
présentées dans le spectre de signal. Nous présentons les
résultats de simulation relatifs à l'analyse par FFT en
régime permanent à charge nominal, dans les figures qui suivent
:
Frequency content of y
300
250
200
150
100
50
0
0 50 100 150
frequency (Hz>
0 50 100 150
300
250
200
150
100
50
0
Frequency content of y
frequency (Hz>
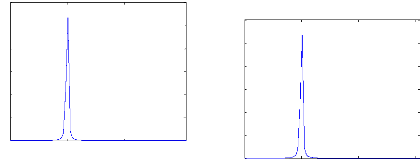
Figure III.17 : Moteur sain à vide Figure III.18 : Moteur
sain en charge
Frequency content of y
25 30 35 40 45 50 55 60 65 70
frequency (Hz>
Frequency content of y
200
150
100
50
0 10 20 30 40 60 70 80
50
frequency (Hz>
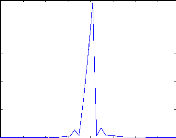
Figure III.19 : Moteur avec une barre cassée Figure III.20
: Moteur avec deux barre
cassées
Les figures III.17 à III.20 présentent le spectre
de fréquence du courant autour de 50Hz.
Lors de la simulation du moteur sain, à vide et en charge,
nous n'observons aucune raie latérale figure III.17 et III.18.
Lorsqu'une barre est rompue, on remarque l'apparition des raies
latérales à 46 Hz et 54 Hz au voisinage du fondamental
fs = 50Hz, figure III.19.
Si on augmente le nombre de barres casées (K=0 ; K=1), on
obtient des valeurs importantes de l'amplitude des raies figure III.20.
Donc une analyse spectrale du courant statorique fait
apparaître les composantes latérales par rapport au fondamentale
à 46 Hz et 54 Hz correspondantes à la fréquence de
Deleroi fs (1 #177; 2.g) [10].
Ce résultat très important constitue une signature
fiable du défaut.
III.4 Conclusion
Dans ce chapitre, on a donc exploite la flexibilité du
modèle initial pour prendre en compte les défaillances rotoriques
pouvant affecter la machine asynchrone triphasée a cage
d'écureuil.
Nous avons simulé la machine asynchrone en premier lieu,
avec des défauts au rotor puis on a fait une analyse harmonique des
courants statoriques.
Nos simulations nous permettrons de conclure, que la cassure
de barres fait apparaître des oscillations sur le courant, le couple et
la vitesse. D'autre part ce défaut connaît un effet cumulatif lors
de la rupture de barre.
Une analyse harmonique des courants statorique permet de voir une
corrélation entre le défaut et les amplitudes des composantes
à fs (1 #177; 2 . g) .
On a montré que ce modèle pouvait répondre
aux objectifs fixés :
compréhension des phénomènes physiques
mis en jeu et prédiction de la dégradation des performances lors
de l'occurrence de défaillances, extraction et analyse des signatures de
défaillances.
| 


