II.3.1.3. Stator Rotor
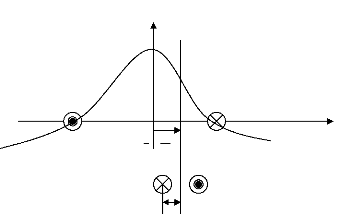
L'induction produite par la bobine statorique de la phase
m induit dans la maille rotorique K le flux :
|
è
+
p
|
k
|
2 ð
N r
|
ð
+
N r
|
|
Ö
|
smrk
|
r r
B dS = -
sm rk
? ?
|
B sm
|
( ' ) '
è LRd è
|
(II.7)
|
N N
r r
k
Srk
è
+
p
2 ð
ð
è ð ð
2
+ k +
r
1

[ ?]
? - ? N N r
2 ð
0 p
N I LR sin '
? p m
è (II.8)
ð ep
s sm p ? 3 +

? è ð ð
2
k -
Bs
0
p
Nr Nr
Ir 0 Phase a
è
è k 2 ð
+
Nr
ð
Irk Maille rotorique k
Ñ
Nr
Figure II.4 : Position de la maille
rotorique K , par rapport à la bobine
de la phase statorique
( m = 0)
Il en résulte la mutuelle stator rotor entre la phase
statorique m et la maille rotorique K :
(II.9)
2 ð ?
M smrk M sr è m
= - ? -
cos ?? + k á ??
3
Où M = 0 Ns LR
sin á
sr 4 u
2
ep 2
(II.10)
Et á = p 2ð est
l'angle électrique entre deux mailles rotoriques.
Nr
II.3.2. Mise en équation
Nous utilisons une transformation de Clarke pour passer des
grandeurs triphasées statoriques ( a, b, c ) aux grandeurs
diphasées ( á â ) . Nous pouvons effectuer la
simulation avec deux repères distincts pour le stator et le rotor.
Pour alléger le temps de calcul, on élimine
l'angle è de la matrice de couplage en choisissant le
repère le plus adéquat et qui est celui du rotor. Dans ce
repère, toutes les grandeurs ont une pulsation gùs en
régime permanent. Cette caractéristique peut être
utilisée pour l'analyse de rupture de barres rotoriques dans la machine
par l'observation du courant ids .
II.3.2.1. Stator
On déduit pour l'ensemble des phases statoriques
[ V sabc ] = [ Rs][ I
sabc]+ dt[ Ö sad (II.11)
Après transformation et rotation, les équations
électriques dans le repère rotorique s'écrits :
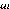
V ds = Rs ids -ù
Ö qs +dÖ ds
dt
(II.12)

dt
V = R iqs +ùÖds
+dÖqs
(II.13)
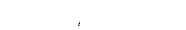
L
L
cos
sin
? ?
M sr
?? - ??
0
Lsc
ids
Ösdq
qs
0
Lsc
Avec :
Nous obtenons :
? ?
? I r 0
? ?
? M ?
j á L ? Ò (II.14)

I rj
? ?
j á L Òÿ? Ò
? ?
? M ?
? ?

?
Ir (Nr
- 1 ) ?

dI
di
dI
dI
(N - 1 )
r
ds
)
Msr
0 + cos 1á r1 +
+ cos já rj+ + cos(
Nr-1)á
dI
Lsc
dt
d t dt
dt
dt
(II.15)
(cos 0á
V ds =Rs ids
- ù[ Lsciqs - Msr (sin
0á Ir0 + sin 1á
Ir1 + + sin já I+ + sin(
Nr - 1)á Ir
(Nr- 1) ).]
+ ù [ L i M
- (cos 0 á I + cos 1 á I + +
cos j I
á + +
cos( 1)
N - á I ( N - 1 ) ) ]
sc ds sr r 0 r 1 rj r r r
dI
r 0 r 1 rj
+ 1 + + i j + + sin( 1)
N - á r
dt dt dt
sin
dI
d i
qs
+
-
dt
(sin 0 á
M sr
Lsc
)
(N - 1 )
r
dI r

dt
(II.16)
dI
On écrit les équations sous la forme :
[ ] [ I ] [ V ] [ R ][ I]
d
L = - (II.17)
dt
Donc :
di
dI
)
( -1)
N
r

ids
R s
Vds
dt
(II.18)
dI dI
Lsc
ds r 0 rj r
- M (cos 0 á + +
cos j á + +
cos( 1)
N - á sr r
dt
dt dt
0á I r0 + + sin
já I + + sin( N r - 1)á I r
-
+ù
ù
i qs
M sr
(sin
L sc

)
( -1)
N
r
Et :
d i
qs
M sr
Lsc
dt
dI
dI
0
(sin 0á r
+ sin já rj+ + sin(
Nr-1)á dI ) V s R
r (N -1)
= s iQs
dt dt dt (II.1 9)
|
-
|
ù
|
L sc
|
i ds
|
ù
M sr (cos 0á I
r0 + + cos já
|
I + + cos( Nr -1)á
Ir
|
(Nr-1) )
|
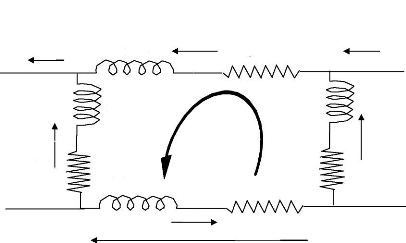
II.3.2.2 Rotor
une maille du rotor à cage est représentée
par la figure II.5
Irk
Ir(k+1)
Re/Nr
2 1
Ir(k-1)
Lb(k-1)
Lbk
Ibk
Irk
Ib(k-1)
Rb(k-1)
Rbk
3 Iek 4
Le/Nr
Re/Nr
Le/Nr
Figure II.5 : Représentation d'une maille rotorique
IeIrk représente le courant de maille K ,
Ibk le courant de la barre K .
Pour le noeud n° 1 :
Ibk = I rk - I r( k
+1) (II.20)
Pour le noeud n° 2 :
I b k = I r k - - I rk
( 1 )
- (II.21)
( 1 )
L'équation électrique relative à la maille
K est :
R [ ] [ ] [ ] dt
R d Ö
e e rk
0 = -
I R I - +
I I I R I I
- + - + (II.22)
rk b k
( 1 ) ( 1 )
- r k - rk rk e bk rk r k
( 1 )
+
N N
ü r
Donc l'équation électrique relative à la
maille K devient :
0 = R e I rk -I R+R
e [ I rk - I e Ibk Rbk+ dÖ
(II.23)
b(k - 1 ) b(k -1)
NN
dt
r r
Le flux induit dans la maille rotorique est donné par :

rk = rprk+ M ?I j - 2 3
Msr (cfr cos Ká + i
qs sin Ká)+ e (I
rk I ek ) + L b(
j
, b( k- 1)
+Ibk) (II.24)
Ö
Nr-1
j ? k
j
?
k
Le terme en Lrp représente le flux principal,
celui en M représente le flux mutuel avec les autres mailles
rotoriques, puis viennent les termes de couplage avec le stator. On remarquera
le facteur 3 2 par rapport à l'équation statorique
à cause de la transformation de Clark.
Les termes en Lb et Le
représentent les fuites rotoriques.
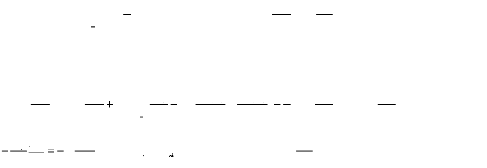
On essaye d'écrire l'équation (II.24) uniquement en
fonction des courants de maille ;
I rk - Ie= Iek (II.25)
Où : Ie représente le courant de l'annau
de court circuit, On a :
dIr( k-1)
dIr( k+1)
dt
dt
(
Lb
Re
-
R bk I r
( k +1)
Ie
? ? ?
Nr
- L I
b [ r k + I r k ] b rk
+ 2 L I
( 1 )
- ( 1 )
+
cos Ká +qs sin
Ká
- R b( k- 1) I(k -
)
2
L e
L e
-
+
Irk
Nr
Nr
2
Le
on aboutit à :
+ 2L b)dIrk
dt
Nr
L +
2
+ R bk +Rb
dIe
Re
?
I ?
?
Le
dt
( k -1)
Nr
Nr
1
dI rj
-
?
M rr
dt
0
k
?
j
j
N r
)
3
(
dids
2
Msr
dt
(II.26)
cos ká + diqs
sin
dt
Ie
)
ká
(II.27)
Ö rk = Lrp rk +
1
-
Nr
M I
rr ? rj
j
j
0
k
?
3
-
2
Msr
(ids
Pour l'anneau de court circuit
Le système complet [L] [ ]
d I
= [ V ] - [ R][ I] devient :
Nr -1N r - 1
dI L dI R ?
e e rk e
- ? = - ? -

L ? R I ? I ?
(II.28)
e e e rk
dt N dt
r k = 0 ? N r k = 0 ?






1 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
0 L L L -M sr cosjá
0
L ssc

L L


sinjá L L
0
0
Lsc
Msr
L
L L
-
?
ids
2L
L e
iqs
M
M
2 L M L
-
b rr b
M L M M L
rr b
-
rr rr
L
+ + e Nr
-
rp
Nr

2Le
I r 0
M
M
M
2 L M
b rr
Mrr-Lb
Lrp
Lb
M L M rr rr
+ +
Nr
-
d
M
3 3
- M k
cos á - M k
sin á
sr sr
2 2

M
dt


I rj
M
M
M
M

Ir Nr (
2Le
Le
1
-
M
M
2Lb
Lb
Mrr
Mrr
Mrr-Lb
Lrp
M
+ +
Nr
L
-
-

rr
Nr
?
?
I e
Le
L e
0 0
L e
L
L
L L
-
-

Nr
Nr
?
M srùsinjá
Rs - ùLsc
0
1 ?
?
?
?
?
?
?
?
?
?
? ?
L
L
L
L
Vds
Vqs

1 ? ? ? ? ? ? ? ? ? ? ? ?
ids
ùLR
sc s
Ms
0
r ù á
cos j
L
L
L
L
iqs
Re
Re
0 0 2
+ Rb0 + Rb( Nr - 1)-Rb0
Nr
-
0 0
R b Nr
(

? ? ? ? ? ? ? ?
1)
-


0
-

Ir0
Nr

M
0 0
0
M

Re
-
M
0 0
0
2
+Rbk +Rb(k
0
Rb k
Rbk
0
( -1)
1)
-
Irj
-
Nr


M
0 0
0
M

R e
Rb(Nr -2) 2 + R b Nr
Nr
Re
0
Ir( Nr-1)
0 0
0 0
(
- 2) ( 1)
+ R b Nr -
Rb(Nr -1)


-

Nr

L
0
Ie
R
R
0 0
R e
e
e
L
L L
-
-

Nr Nr Ò ÿ
Nr
Nr
? ?
(II.29)
Le couple électromagnétique est obtenu par
dérivation de la co-énergie:
? ? ?
? ?
1
Irk M
M
3 ä? L - M cos( )
è á
+ k L sr
= P i
[ ] t
2 sdq ??L - cos( )
è á
+ L ??
äè M k
sr
Cem
- r
3
C = PM i I k
? Nr ? 1 N 1
-
? sin á - ?
i I k
cos á (II.31)
em ds
sr rk qs rk
2 ? k = 0 k = 0 ?
On y ajoute les équations mécaniques afin d'avoir
la vitesse ? = ù
P
d? 1
dt P
= J em - r -
P C C
( ù ) (II.32)
f
d è =
Et ù
Le système ci-dessus est très compliqué
pour le programmer et l'exécution d'une simulation d'un tel
modèle est très lente, c'est pour cela qu'on a opté pour
un autre modèle, le modèle dq .Nous avons
appliqué une transformation généralisée (
Nr ) qui permet de passer des Nr
grandeurs équilibrées vers deux grandeurs dq . La
simulation de ce modèle est très rapide.
II.4. La transformation de N
grandeurs équilibrées en deux grandeurs
dq [6] r
d Ir0
Ir1
Ir15
è 2ð / 16
Ir2
Ir14
I1
Ir3
â
Ir13
Ir12
q
Ir5
r11
Ir1
Ir6
Ir10
Ir8
Ir9 Ir7
Ir4
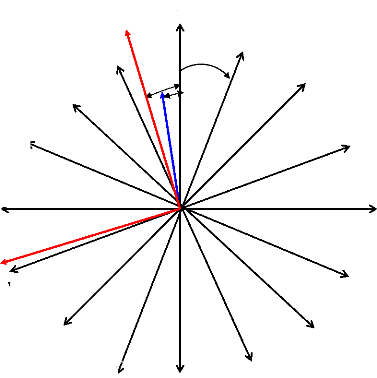
Figure (II.6) : projection du modèle multi enroulement sur
le modèle dq > Passage du modèle
polyphasé au modèle biphasé
On calcule les différentes résistances
équivalentes ( S 1 , S 2,
S3, et S4) ;
|
2 ? R ? R ?
2 e 2 + + ? +
e
= ? + + R ?
e
S ? 2 R R cos 0 2
+ ? + +
? á ? R R
cos 1
? á L ? 2
R R
+ ? cos 15
2 á
1 b 0 b 15 b 1 b 0 b
15 b 14
16 N
[ ? ? N ? ? N
r r r ?
|
1 ? ?
|
- [ (
4 R cos 0 cos 1
á á ) (
+ R cos 1 cos 2
á á ) (
+ L + R cos 15 cos 0
á á ]
) (II.33)
b 0 b 1 b 15
16
i
i

0
Rs - ùLsc 0 - Nr ùMsr
2
(II.37)
Nr
ù L sc Rs - ùMsr
0 Re
Rr
0
Rr
0 0
0 0
2
0 0
1 ? ? ? ? ? ? ? ? ?
0 0 0
0 0 0
R
Avec : = 2 + 2 Rb ( 1 - cos
á)
e
R r
Nr
S 2 = - 2 [(2 R e + A0
+g15 jcos0 ásin0 á -(2 R
e +R +g0 jcos1 á sin1
á (2 R e + k5
+Rb14)cos1 5ásin1
6 r r
N Nr
2 rf
+ 6 RR b 0 sin 0 á cos
1á ) + (Rb1 sin 1 á
cos 2á ) +
·
·
· +
(Rb15 sin 15á cos 0á)]
2 rf
i
i
+ 6 RR b 0 cos 0 á sin
1á ) + (Rb1 cos 1 á
sin 2á ) +
·
·
· +
(Rb15 cos 15á sin 0á)] (II.34)
Re
S 3 = - 6[(2 +A0
+g15 jcos0 á sin0 á
-(2 +R +R jcoslasinla-- -
N
r -
· '(
2 Al5+
N #177;r Rb14)cos1
5ásin1
Nr
2 R e Re
2 rf
+ 6 RR b 0 sin 0 á cos
1á ) + (Rb1 sin 1 á
cos 2á ) +
·
·
· +
(Rb15 sin 15á cos 0á)]
2 rf
+ 6 RR b 0 cos 0 á sin
1á ) + (Rb1 cos 1 á
sin 2á ) +
·
·
· +
(Rb15 cos 15á sin 0á)] (II.35)
|
S 4 = 12 6 [(2 e +
R615 cos2 0 á + 2 N R
: + RbI +
Rb0 cos2 1á +
·
·
· + 2
NR: + R ,,,, +
RbI4 cos2 15á
NR + Rb0 r )
( L,=, JJ
|
1 1
i
|
1 ri
- Rb 0 cos 0 á cos
1á ) + (Rb1 cos 1 á
cos 2á) +
·
·
· +
(Rb15 cos 15á cos 0á)] (II.36)
4 6
Si l'on considère que toutes les barres sont saines (
Rb 0 = Rb1 = = Rb15), les
résistances
équivalente S1 , S
2 , S3 , et S 4
Deviennent :
|
S 1 = S4
|
2 Re + 2Rb (
1-- cosá)
Nr
|
R
S 2 = S 3 = 0 , En posant : = 2 + 2
Rb ( 1 - cos á)
e
R
r
Nr
La nouvelle matrice de résistance du modèle
dq équivalent, en considérant que toutes les barres sont
saines est [4] :
0 3 Msr
2
0 0
Nr
-
2
0 Lsc 0
3 Msr
2
Avec :L = L -Mrr + 2 Le +
2Lb( 1-cosè)
p Nr (II.38)
-
Msr 0 0
Nr M sr
2
0 Ò

0 Lrc 0 0
0 Lrc 0
0 0
Lsc 0

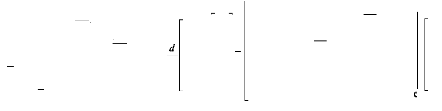
Donc le modèle réduit, en considérant que
toutes les barres sont saines est :
?
0
ids
0 0
0 0
0 Rr 0
0 0 R
iqs
idr
iqr
Ie
e Ò ÿ
0
Vds
Vqs
idsi qsidri qrIe
1
? ? 0 ?
Nr
Rs - ù L sc 0 - ù M
sr
2
Nr
ù L Rs
sc - ù M sr
2
0 0 Rr 0 0
0 0
? ? ? ? ? ? ? ?
-
2
3 Msr
Lsc
0 Lsc 0
0
0 0
2
3 Msr
0
0 Lrc 0 0
-
Nr
2
0 Lrc 0
0 0
Msr
Nr
2
0 0
Msr
?
?
?
?
?
?
?
?
Le]
0
dt
(II.39)
II.5 Contrôle des courants par
hystérésis :
Le principe de cette méthode de contrôle des
courants par hystérésis est basé sur la commande des
interrupteurs de l'onduleur de telle sorte que les variations du courant dans
chaque phase du moteur soit limitées dans une bande
d'hystérésis encadrant les références des
courants.
Ce contrôle se fait par une comparaison permanente entre
les courants réels et les références de courant. La sortie
des comparateurs est reliée à la logique de commande de
l'onduleur de manière à imposer une commutation des interrupteurs
lorsque le courant s'écarte de la valeur d'hystérésis de
sa référence.
Les ondulations du courant sont fixées par la valeur de
la bande d'hystérésis. Dans cette méthode le courant est
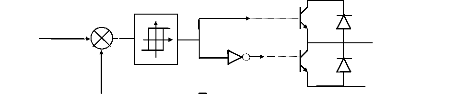
toujours imposé aux bornes de la machine. La figure (II-7) donne le
schéma de principe.
Ti
+
-
i ref
Ti'
inverseur
Comparateur à hystérésis
Bras de l'onduleur
i
Figure II.7 :Principe du contrôle des courants par
hystérésis
II.5.1 Modélisation de l'onduleur
L'onduleur est un convertisseur statique assurant la
conversion continu - alternatif, il est composé de six transistors
(T1,...,T3,T'1,...,T'3) shuntés en anti-parallèle par des diodes
de récupération (D1,...,D3,D'1,...,D'3), qui permettent de
renvoyer le courant négatif vers le condensateur de filtrage mis
à l'entrée de l'onduleur .

+ 1
F i 0
=
si K est fermé et K ouvert
'
i i
si Ki est ouvert et K fermé
i '
? ? ?
(II.40)
Les tensions de ligne aiguillées par l'onduleur sont :
U
= 2 (F1 - F2 )
U
. (F2 - F3)
2
U
. ( - F 1 )
F3
2
Uab
Ubc
L
Uca
(II.41)
La relation imposée par la machine aux tensions de phase
s'exprime par :
Va + Vb + Vc = 0 (II.42)
En tenant compte de cette relation, on déduit les tensions
simples :
|
?
?
?
? ?
|
Va
Vb
V c
|
1 ?
? U . ?
=
? 3 ?
? ? ?
?
|
2 - 1 -1 1 2 -1 1 -1 2
|
? ?
? . ?
? ?
? ? ? ?
|
F 1
F2
F3
|
1
?
?
? ?
|
(II.43)
|
II.5.2 Modélisation du modulateur à
hystérésis
Pour déterminer les signaux de commande des
interrupteurs de l'onduleur, il suffit d'associer un modulateur à
hystérésis pour chacune des trois phases de l'onduleur, ceci
permet de comparer chaque courant de phase avec sa référence de
courant sinusoïdale de telle sorte que la variation de courant dans chaque
phase soit limitée dans une bande encadrant la référence
des courants :
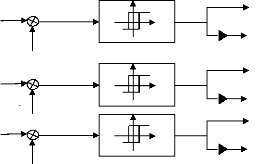
ib
Irefb
+ _
_
ic
Irefa
+ _
ia
Irefc
T1
T1'
T1
T2'
T1
T3'
Figure II.8
Les fonctions logiques représentants les interrupteurs de
l'onduleur sont définis par :
La commutation des composants électriques est
supposée instantanée (composants parfaits).Afin
de simplifier l'étude, nous associons à chaque bras
de l'onduleur, une fonction
logique Fi(i=1,2,3) qui est la sortie du modulateur
Hystérésis.
Les fonctions logiques sont définies ainsi :
i
Fi = 0 si ij-ijref > h
Fi = 1 si ij-ijref >- h (II.44)
Fi = Fi si ijref+h >ij> ijref-h
Avec ij courant de phase, j = a,b,c et ijref courant
de référence II.6 Simulation du modèle
réduit multi enroulements :
a. Cas d'une machine saine à vide : 1.
Alimentation sans onduleur :
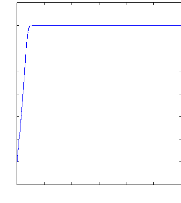
0 0.5 1 1.5 2 2.5 3
t(s)
1
n(trLm n)
3500
3000
2500
2000
1000
-500
500
500
0
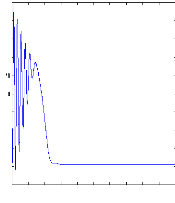
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t(s)
1
Cem(N.rn)
18
16
14
12
-2
6
4
2
0
Figure II.9 : vitesse de rotation, couple
électromagnétique, simulation
avec le modèle
réduit, machine saine en charge, Cr=3.5 N.m
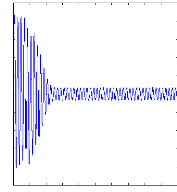
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
ias(A)
-15
-2 0
-10
-25
25
20
15
10
-5
5
0
t(s)
Figure II.10 : courant statorique, simulation avec
le
modèle réduit, machine saine à vide
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t(s)
irbO(A)
-1000
1500
1000
1500
-500
500
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t(s)
irb(A)
-1000
-1500
1500
1000
-500
500
0
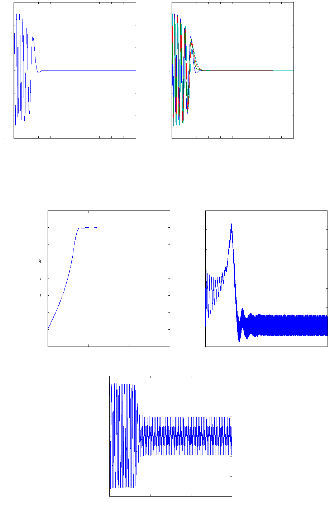
Figure II.11 : courants dans les barres rotoriques,
Irb0,Irb1,Irb2,Irb3,
simulation avec modèle global, machine saine
à vide
2. Alimentation avec onduleur :
0 0.5 1 1.5
nitrim n)
1
1
2500
3500
3000
-500
500
000
500
000
0
0 0.5 1 1.5
Cem(N.m )
12
10
-2
8
6
4
2
0
t(s)
0 0.5 1 1.5
t(s)
las(A)
-10
-15
15
10
-5
5
0
t(s)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t(s)
irb 0(A )
-1000
1500
1000
1500
-500
500
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t(s)
irb 3(A )
-1000
-1500
1500
1000
-500
500
0
0 0.5 1 1.5 2 2.5 3
t(s)
n(trlin n)
1
35 00
30 00
25 00
20 00
10 00
-5 00
5 00
5 00
0
0 0.5 1 1.5
t(s)
C em (N A )
18
16
14
12
-2
0
8
6
4
2
0
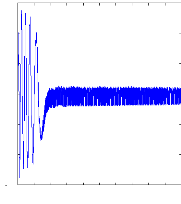
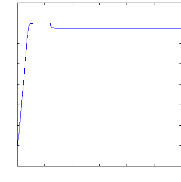
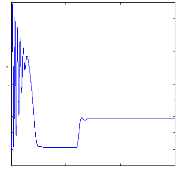
Figure II.12 : simulation du modèle réduit,
Alimentation avec onduleur àvide
A vide :
On n'impose tout d'abord aucun couple de charge et la machine
opère donc a vide. La
Figure( II.9) illustre l'évolution temporelle, en
régime transitoire et en régime permanent, de la vitesse de
rotation, après une phase transitoire, celle-ci se stabilise a une
valeur proche de la vitesse de synchronisme a cause de l'absence d'un couple de
charge, la figure illustre aussi le couple électromagnétique .
Pour le couple, après une phase transitoire, celui-ci se stabilise comme
convenu a une valeur proche de zéro a cause de l'absence d'un couple de
charge. La figure( II.10) illustre l'évolution temporelle, en
régime transitoire et en régime permanent du courant statorique
en absence du couple de charge. La figure (II.11) illustre l'évolution
temporelle, en régime transitoire et en régime permanent, des
courants de barres rotoriques Irb0 , Irb1, Irb2, Irb3. On constate
que les barres rotoriques sont parcourues par des courants faibles mais non
nuls en régime permanent. On peut expliquer cette circulation de
courants par l'existence d'un frottement visqueux qui génère un
faible couple résistant, et par l'existence de champs harmoniques ne
tournant pas, par définition, a la vitesse de synchronisme. Les boucles
rotoriques soumises a des champs fluctuants sont alors le siège de
courants induits.
b.Cas d'une machine saine en charge :
1. Alimentation sans onduleur :
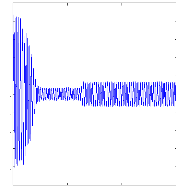
ias(A )
· 10
· 15
· 20
· 25
25
20
15
10
· 5
5
0
0 0.5 1 1.5
t(s)
Figure II.14 : courant statorique, simulation avec
le
modèle réduit, machine saine en charge,
Cr=3.5N.m
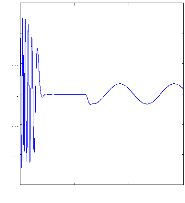
0 0.5 1 1.5
t(s)
irbO(A)
· 1000
· 1500
1500
1000
· 500
500
0
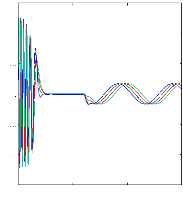
0 0.5 1 1.5
t(s)
irb(A)
· 10 00
· 15 00
1500
1000
· 500
500
0
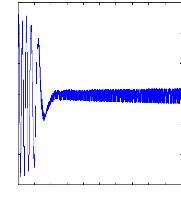
Figure II.15 :courants dans les barres rotoriques,
Irb0,Irb1,Irb2,Irb3, 2. Alimentation avec onduleur :
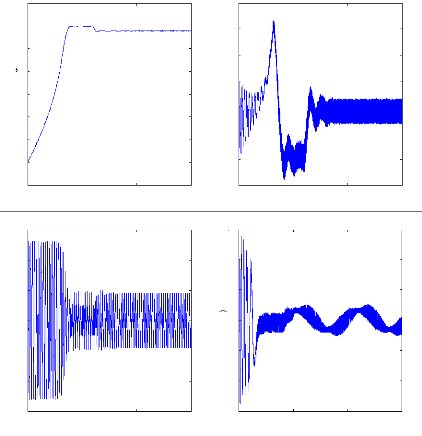
12
10
8
6
4
Cem(N.m)
2
0
-2
1 5
10
5
0
ia s(A )
-5
-10
-15
500
1000
500
0
irb 0 (A
-500
-1000
-1500
0 0.5 1 1.5
t(s )
0 0.5 1 1.5
t(s)
0 0.5 1 1.5
t(s)
0 0.5 1 1.5
t(s)
3500
3000
2500
000
500
000
k(trim n )
1
1
500
0
-500
Figure II.16 : simulation du modèle réduit,
Alimentation avec onduleur en charge En charge :
On impose maintenant un couple de charge de 3.5 N.m et la machine
opère alors
en charge. La figure (II.13) illustre l'évolution
temporelle, en régime transitoire et en régime permanent, de la
vitesse de rotation, après une phase transitoire, celle-ci se stabilise
a une valeur de 2885 tr/mn, la figure illustre aussi le couple
électromagnétique . Pour le couple, après une phase
transitoire, celui-ci se stabilise comme convenu à une valeur proche de
3.5 N.m.
La figure(II.14) illustre l'évolution temporelle, en
régime transitoire et en régime permanent, du courant statorique
en présence d'un couple de charge de 3.5 N.m.
La figure(II.15) illustre l'évolution temporelle, en
régime transitoire et en régime permanent, des courants de barres
rotoriques Irb0 , Irb1 , Irb2, Irb3. On constate que les
barres rotoriques sont logiquement parcourues par des courants de
fréquence fondamental g fs0 en régime permanent. Ceux-ci
possèdent également une fréquence fondamentale g fs0 en
régime permanent.
II.7 Conclusion
Dans ce chapitre on a traité la machine asynchrone en
terme de circuit, et on a considéré que le rotor est
constitué de plusieurs éléments, chaque
élément de la cage est décrit par un circuit
électrique équivalent de Nr grandeurs. Puis, on a fait la
transformation de Nr grandeurs vers deux grandeurs, pour faciliter
l'étude.
On remarque que la méthodologie de modélisation
adoptée est assez générique, et peut très bien
être adaptée pour la représentation d'autres types de
machines électriques : machines asynchrones a rotor bobiné,
machines synchrones a aimant permanent ou a rotor bobiné, machines a
reluctance variable. Cette modélisation peut également servir
dans une certaine mesure a des objectifs de conception.
Le modèle constitué donne des résultats
identiques à ceux obtenus dans le cas du modèle classique de la
machine asynchrone et permit d'étudier les différents
défauts rotoriques, donc ce modèle s'adapte bien au
problème posé.
Dans la suite de l'étude, on va plutôt exploiter
la flexibilité du modèle pour rendre compte d'un certain nombre
de défauts rotoriques pouvant affecter les machines asynchrones
triphasées a cage d'écureuil.
| 


