Chapitre II
Modélisation du schéma
multienroulements de la machine
asynchrone
II.1 Introduction
Les machines asynchrones à rotor en court-circuit
consomment plus de 40% de l'énergie
électrique produite ;
elles sont largement utilisées vu les avantages qu'elles
présentent à savoir :
- leur simplicité et leur robustesse mécanique,
- leur fonctionnement sans génération
d'étincelles d'où un entretien réduit,
- la normalisation des réseaux de distribution de
l'énergie électrique se prête bien à l'utilisation
directe de ces moteurs (tensions et fréquences constantes),
- un prix de revient relativement faible.
Par ailleurs, la machine asynchrone, malgré ses
qualités, peut présenter des défauts structurels. Dans ce
chapitre, nous portons notre attention sur la rupture totale ou partielle de
barres rotoriques, tout particulièrement au niveau de la brasure barre-
anneau. Pour ce faire, il convient de développer un modèle qui
tienne compte de la structure du rotor.
En effet, Pour étudier ces machines à induction on
fait appel soit à la théorie du champs
électromagnétique (équations de Maxwell), soit à la
théorie des circuits électriques (lois de Kirchhoff) ; ou bien la
méthode mixte combinant la théorie du champ
électromagnétique et la théorie des circuits
électriques [7].
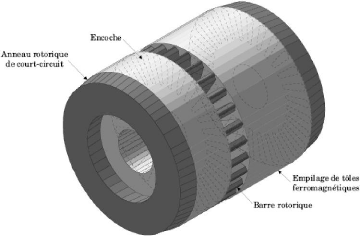
Figure (II.I) : constitution et disposition d'une cage rotorique
[1]
Il est fonction du type d'approche utilisée. On en
distingue deux , assez complémentaires :
- une approche dite << locale > car basée sur
la signature de grandeurs locales telles que la densité de flux ; il
s'agit souvent de méthodes numériques par éléments
finis permettant une analyse fine des phénomènes physiques locaux
associés aux défauts de cages,
- une approche analytique basée, quant à elle,
sur la signature de grandeurs externes globales telles que courants, couple
électromagnétique ; elle utilise le modèle de Kirchhoff,
(réseau électrique équivalent à la machine) ainsi
que la transformation << des 2 axes > appliquée aux
équations électriques du système multi enroulements
étudié. En fin, cette approche s'adapte particulièrement
bien au problème posé ici et vu sa simplicité nous l'avons
adoptée comme démarche.
II.3 Schéma multi enroulements
équivalent
Pour l'étude analytique des performances des moteurs
d'induction avec dissymétries rotoriques, nous avons adopté le
schéma multi enroulements équivalent qui s'adapte bien au
problème posé, car il décrit le rotor comme un ensemble de
mailles interconnectées entre elles, chacune formée par deux
barres adjacentes et les portions d'anneaux qui les relient (figure II.1).
A partir d'hypothèses classiques qui supposent que la
perméabilité du fer est infinie, que l'entrefer est lisse et
constant et que la f.m.m. statorique est à distribution
sinusoïdale, on calcule les différentes inductances et mutuelles
qui interviennent dans les équations du circuit.
II.3.1 Calcul des inductances [4] II.3.1.1
Stator
L'induction due à la bobine statorique de la phase m
s'écrit :
|
?
??
|
(II.1)
|
|
|
|
B sm
|
2 N ? - 2 ð
s
( ) 0
è = u I cos ?? p m
sm è
ð ep 3
|
Par conséquent, le flux principal et l'inductance cyclique
sont donnés par :
Ö
2
= 4 p oNs RLI
(II.2)sm
psmð ep2
L = 3 L sl 0 Ns
sc 2 sp +1 = p ep2 RL+
6


Lsl (II.3)
II.3.1.2 Rotor
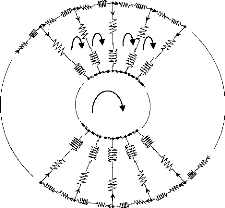
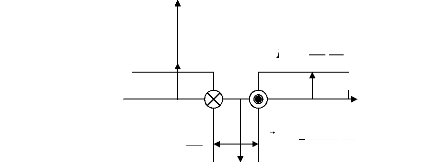
Le rotor à cage est représenté par la figure
II.2. La figure II.3 représente la forme d'onde de l'induction produite
par la maille rotorique k.
Ir(k-1)
Ir(k-2) Ir(k+1)
Ie
Irk
Figure II.2 :
Schéma multi enroulements du rotor
2ð
0
a r
I bk = I rk - Ir ( k
+ 1 ) (II.4)
r
r 1 u
2 rk = N e0 Irkar r
è
Nr -1 u0 Irkr
ar
N e
r
2ð
Nr
Irk
B 1
rk =
Irk Représente le courant de maille k et
Ibk le courant de barre K , avec :
On voit bien, à travers la figure II.2 qu'il n'est pas
possible de retenir l'hypothèse du premier harmonique qui concerne
l'induction produite par une maille du rotor. Partant de cette
répartition, on calcule alors l'inductance principale d'une maille
rotorique ainsi que la mutuelle entre deux mailles :
L rp
M rr
N
(II.5)
(II.6)
r -1 u0 2
= ðLR
1
Nr 2 e
= - u 0 2ff,LR
N 2 e
| 


