VI.5 Conception d'un régulateur flou de vitesse
Nous allons maintenant illustrer les principes du
contrôleur flou sur l'exemple de la régulation de vitesse de la
machine asynchrone. La phase de conception d'un contrôleur flou passe
toujours par quatre stades que nous allons détailler successivement.
· 1 ére étape : Choix des
entrées et sorties
Il s'agit de déterminer les caractéristique
fonctionnelles (1) et opérationnelles (2) du contrôleur.
(1)- Il faut d'abord choisir les variables d'entrée et
de sortie. Leur choix dépend du contrôle que l'on veut
réaliser. Que souhaite-t-on au juste commander ? A l'aide de quels
paramètres va-t-on obtenir la commande ?
(2)-Il faudra ensuite se pencher sur le domaine des valeurs
que pourront prendre ces variables). On partitionnera alors ces domaines en
intervalles, auxquels on associera un label descriptif (variables
linguistique). Cette étape revient à définir les univers
des discours des variables d'entrée et de sortie et les diviser en
sous-ensembles flous. Cette répartition est intuitif et basé sur
l'expérience. On est d'ailleurs généralement amené
à l'affiner en cours de conception. Une règle de bonne pratique
est de fixer 5 à 9 intervalles par univers de discours. Il faut
également prévoir un plus grand nombre de zones à
proximité du point de fonctionnement optimal pour en faciliter
l'approche régulière [43], [44].
Illustration sur le régulateur de
vitesse
Dans le cas de la régulation de vitesse, on a besoin
habituellement de l'erreur (e=?r ref -?r) et de la
dérivée d'erreur (de) et parfois de l'intégration d'erreur
:
|
e k
( ) rref ( ) r ( )
= ? k - ? k
de k e k e k
( ) ( ) ( )
= - - 1
|
(VI.12)
|
La sortie du régulateur de vitesse est la valeur du
couple de référence dans le schéma de la commande
vectorielle indirecte de la machine asynchrone. Si cette sortie est directement
appliquée au processus, le contrôleur est alors appelé
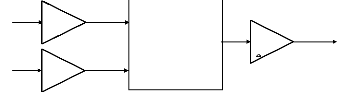
contrôleur flou de type PD [42] et.on peut écrire : Te=
Fuzzy (e, de)
Contrôleur
flou
Kde
Ke
e
de
Kdt
dte
e
de
Kde
ke
kTe
?
Te
Figure (VI.7 ) : Contrôleur flou de type PD
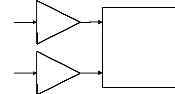
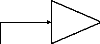
Par contre, si la sortie du contrôleur flou est
considérée comme un incrément de commande, le
contrôleur est appelé contrôleur flou de type PI [42] et on
peut écrire :
? . ?
dte= Fuzzy (e, de) ou encore dte = F uzzy ? e dt de
?? , ?? ;
soit Te ( k ) = dte(k)
+Te(k -1) (VI.13)
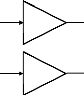
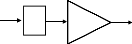
Figure (VI.8) Contrôleur flou de type PI
Contrôleur
flou
e
de
Kde
ke
Kdte
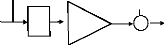
Le contrôleur de type PID peut être obtenu en
combinant des contrôleurs flous de type PI et PD de façon suivante
:
+ Te
?
kTe
+
Figure (VI.9) Contrôleur flou de type PID
On remarque que cette structure de commande flou de type PID
est en fait une association en série d'un contrôleur flou de base
et d'une structure de régulation de type PI, qui, elle, n'est pas floue
[42].
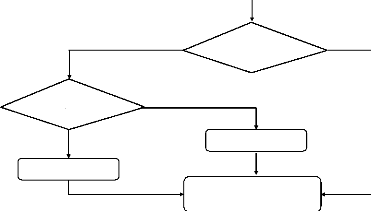
De plus, comme dans la régulation classique, on a
besoin d'une limitation du couple de référence, pour
empêcher une sur utilisation de la machine [36]. Cette fonction peut
être réalisée par l'algorithme de la figure (VI.10).
Comme les fonctions d'appartenance sont normalisées
entre [-1, 1], les variables sont multipliées avec des gains
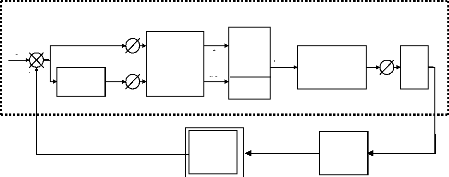
proportionnels. Finalement, la structure du régulateur de vitesse
à logique floue est la suivante :
Calcul de Te(k)
Te(k) = dte(k) + Te(k-1)
oui
Te(k) = Temax
Te(k) > 0
oui
non
|Te(k)| = Temax
Te(k)
variable de sortie
Te(k) = - Temax
non
Figure (VI.10) Algorithme pour limitation deTe(k)
?ref
CONTROLEUR FLOU
+
-
?
Calcul de
de
e
de
kde
k
Fuzzificati
on
Processus
d
de~
Règles
de
contrôle
flou
Inférenc
dte
Défuzzificatio
n
Limitatio
n du
couple
dte
kdte
?
Te
Figure (VI.11) Structure du régulateur de vitesse à
logique floue
D'après ce schéma, le système est
composé :
* du contrôleur flou composé :
· d'un bloc de calcul de variation de l'erreur au cours du
temps (de) ;
· des facteurs d'échelles associés à
l'erreur, à sa dérivée et à la commande (dte);
· d'un bloc de fuzzification de l'erreur et de sa variation
;
· des règles de contrôle flou et d'un moteur
d'inférence ;
· d'un bloc de défuzzification utilisé pour
la variation de la commande floue en valeur numérique ;
· d'un bloc intégrateur ;
* du processus à contrôler.
· 2 éme étape :
Définition des fonctions d'appartenance
La première étape de conception a permis de
cerner au mieux les caractéristiques linguistiques des variables. Il
faut maintenant définir complètement les sous-ensembles flous,
c'est à dire expliciter leurs fonctions d'appartenance. Une fois encore,
l'intuition et l'expérience auront leur rôle à jouer.
Quelques principes ressortent de la pratique: choix de fonctions triangulaires
ou trapézoïdales, recouvrement d'une fonction de 10 à 50% de
l'espace des sous-ensembles voisins, somme des degrés d'une zone de
recouvrement égale à 1 (degré maximal d'appartenance)
[43], [44].
Illustration sur l'exemple
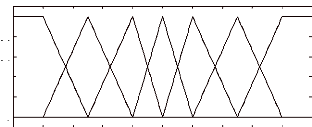
Les fonctions d'appartenance des variables d'entrée sont
illustrées par la figure (VI.14)
avec :
NB : Negative Big (Négative Grand) PB : Postive Big
(Positive Grand)
NM : Negative Medium (Négative Moyenne) PM : Postive
Medium (Positive Moyenne) NS : Negative Small (Négative Petit) PS :
Postive Small (Positive Petit)
ZE : Zero
On constate que les fonctions d'appartenance de l'erreur ont
une forme asymétrique créant une concentration autour de
zéro qui améliore la précision près du point de
fonctionnement désiré.
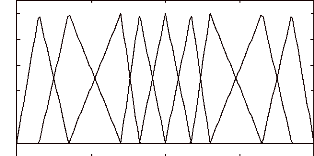
Pour la même raison, les formes des fonctions
d'appartenance de la variable de sortie sont également
asymétriques. Cependant, nous introduisons deux sous-ensembles
additionnels compte-tenu de la sensibilité de cette variable [44].
NVB : Negative Very Big (Négative Très Grand) PVB
: Postive Very Big (Positive Très Grand)
· 3 éme étape :
Définition du comportement du contrôleur flou Cette
étape concerne l'élaboration de la base de règle du
contrôleur. Analyse du comportement dynamique -
Détermination du jeu de règles
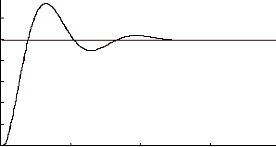
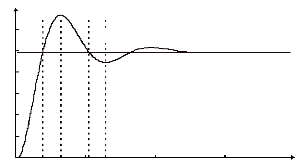
L'analyse temporelle, qui doit conduire à
établir les règles du contrôleur flou, peut par exemple
consister à considérer la réponse à un
échelon d'un processus à piloter en fonction des objectifs que
l'on se sera fixé en boucle fermée, et à écrire les
règles pour chaque type de comportement du processus :
0.8
0.6
0.4
0.2
0
1
Degré d'appartenane u(e)
NB NM NS EZ PS PM PB
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
erreur e
D e g r é d 'a p p a r t e n a n c e u ( d e )
- 1 - 0 . 5 0 0 . 5 1
0 . 8
0 . 6
0 . 4
0 . 2
0
1
N B N M N S E Z P S P M P B
Variation d e l 'e r r e u r `d e '
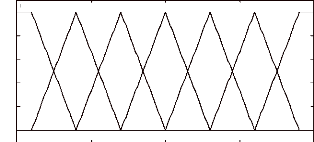
Figure (VI.12) Fonctions d'appartenance des variables
d'entrée
D e g r é d 'a p p a rte n a n c e u ( d te )
- 1 - 0 .5 0 0 .5 1
0 .8
0 .6
0 .4
0 .2
0
1
N V B N B N M N S E Z P S P M P B P V B
Variation d u Couple: `d te '
Figure (VI.13) Fonctions d'appartenance de la variables de
sortie
7
Sortie s

1
temps
·
4
3
·
·
2
·
6
5
·
·
·
·
8 9
Référence
·

Figure (VI.14) Ecriture du jeu de règles grâce
à une analyse temporelle
a)- Pour expliquer la procédure à suivre [42],
on considère les neuf points indiqués sur la réponse
à un échelon et, pour chacun de ces points, on explicite
l'expertise sous la forme suivante :
· 1 Si e = PB Et de = ZE Alors du = PB (départ,
commande importante)
· 2 Si e = PB Et de = NS Alors du = PM (augmentation de la
commande pour gagner l'équilibre)
· 3 Si e = PM Et de = NS Alors du = PS (très faible
augmentation de u pour ne pas dépasser)
· 4 Si e = PS Et de = NS Alors du = ZE (convergence vers
l'équilibre correcte)
· 5 Si e = ZE Et de = NS Alors du = NS (freinage du
processus)
· 6 Si e = NS Et de = NS Alors du = NM (freinage et
inversion de la variation de la commande)
· 7 Si e = NM Et de = ZE Alors du = NM (rappel du processus
vers l'équilibre correcte)
· 8 Si e = NS Et de = PS Alors du = ZE (convergence vers
l'équilibre correcte)
· 9 Si e = ZE Et de = ZE Alors du = ZE
(équilibre)
En décrivant point par point le comportement du
processus et l'action de variation de commande à appliquer, on en
déduit la table suivante (table du contrôleur flou de base) qui
correspond en fait à table de règles très connue de Mac
Vicar - Whelan [42] :
b)- Pour déduire les autres règles ,nous
procédons à nouveau à une autre expertise [45].
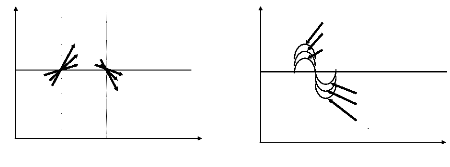
La forme générale de la réponse de
vitesse est représentée sur la figure (VI.16). Selon l'amplitude
de e et le signe de de, la réponse de vitesse est divisée en
quatre régions. Les indices utilisés pour identifier chaque
région sont définies comme suit :
a1 : e > 0 et de < 0, a2 : e < 0 et de < 0,
a3 : e < 0 et de > 0, a4 : e > 0 et de > 0,
|
e
de
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
PB
|
ZE
|
PS
|
PM
|
PB
|
PB
|
PB
|
PB
|
|
PM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
PB
|
PB
|
|
PS
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
PB
|
|
ZE
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
NS
|
NB
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
|
NM
|
NB
|
NB
|
NB
|
NM
|
NS
|
ZE
|
PS
|
|
NB
|
NB
|
NB
|
NB
|
NB
|
NM
|
NS
|
ZE
|
Figure (VI.15) Table de règles de MacVicar-Whelan
Pour identifier la pente de la réponse lors du passage par
le point de référence on utilise l'indice ci défini comme
suit :
|
c1
|
: ( e > 0
|
--* e < 0
|
) et de <<< 0
|
|
c2
|
: ( e > 0
|
--* e < 0
|
) et de << 0
|
|
c3
|
: ( e > 0
|
--* e < 0
|
) et de
|
< 0
|
|
c4
|
: ( e < 0
|
--* e > 0
|
) et de
|
> 0
|
|
c5
|
: ( e < 0
|
--* e > 0
|
) et de
|
>> 0
|
|
c6
|
: ( e < 0
|
--* e > 0
|
) et de
|
>>> 0
|
Quant à l'indice représentatif du
dépassement de la consigne, il est défini par :
|
m1 : de
|
0
|
et
|
e <<<
|
0
|
m4 : de
|
0
|
et
|
e > 0
|
|
m2 : de
|
0
|
et
|
e <<
|
0
|
m5 : de
|
0
|
et
|
e >> 0
|
|
m3 : de
|
0
|
et
|
e <
|
0
|
m6 : de
|
0
|
et
|
e >>> 0
|
Les trois types d'indices mentionnés ci-dessous peuvent
être combinés et former un plan d'état. Le tableau de la
figure (VI.17) est légèrement modifié pour tenir compte
que la variable de sortie est formée de neuf valeurs floues.
|
e
|
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
de
|
NB
|
NVB
|
NVB
|
NVB
|
NB
|
NM
|
NS
|
ZE
|
|
NM
|
NVB
|
NVB
|
NB
|
NM
|
NS
|
ZE
|
PS
|
|
NS
|
NVB
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
|
ZE
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
PS
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
PVB
|
|
PM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
PVB
|
PVB
|
|
PB
|
ZE
|
PS
|
PM
|
PB
|
PVB
|
PVB
|
PVB
|
Figure (VI.16) Base de règles du régulateur I de
vitesse
Réponse
1.4
a1 a2 a3 a4
Référence
temps
0.5 1 1.5 2
1.2
1.0
0.8
0.6
0.4
0.2
0
a)
? réponse ?
C1
C2
référence
C4
C5
C6
temps
b)
C3
m6
temps
réponse
m2
référence
c)
Figure (VI.17) Comportement dynamique de la réponse de
vitesse
|
e
de
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
NB
|
|
c1
c2
c3
|
|
|
a1
|
|
|
a2
NS
|
|
NM
|
|
|
|
ZE
|
m1 m2 m3
|
ZE
|
m4 m5 m6
|
|
PS
|
|
c4
c5
c6
|
|
|
a3
PB
|
|
|
a4
|
|
|
PM
|
|
|
|
Figure (VI.18) Règles linguistiques de contrôle
Dans le tableau (VI.16), chaque élément formalise
une règle comme, par exemple : Si [ e(k) est NM ] Et [ de(k) est ZE ],
ALORS [ dte(k) est NM ].
Cet ensemble de règles regroupe toutes les situations
possibles du système évaluées par les différentes
valeurs attribuées à e et à sa variation de et toutes les
valeurs correspondantes de la variation de la commande dte.
L'évaluation des gains proportionnels provient de
l'expérience. Pour le gain Ke , par exemple, on peut commencer avec un
facteur qui dépend de l'erreur maximale. Effectivement ces valeurs font
partie de la procédure d'évaluation par simulation. On a
trouvé les valeurs suivantes pour la machine asynchrone simulée
:
Ke = 0.1 Kde = 0.6*10-5 Kdte = 65
Dans une deuxième approche d'un régulateur à
logique floue, on utilise différentes fonctions d'appartenance pour la
variable de sortie (figure VI.21):
Degré d'appartenance u(dte)
1 NVB NB NM NS ZE PPS PM PB PVB
0.5
0
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
Variation du couple `dte'
Figure (VI.19) Fonctions d'appartenance de la variable de sortie
dte(k) (II)
Grâce à cette fonction d'appartenance,
appelée «singleton », on tire profit du calcul de la variable
de sortie. Dans ces conditions, la formule du centre de gravité se
simplifie par :
m

=
i
=
i
=
1
m
? u ( )
dte i
1
(VI.14)
dteres
m étant le nombre totale de règles.
Par rapport à la première approche, les
règles sont aussi modifiée
|
e
|
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
de
|
NB
|
NVB
|
NVB
|
NVB
|
NB
|
NM
|
ZE
|
ZE
|
|
NM
|
NVB
|
NVB
|
NB
|
NB
|
NM
|
ZE
|
PS
|
|
NS
|
NVB
|
NB
|
NB
|
NM
|
PS
|
PB
|
PM
|
|
ZE
|
NVB
|
NB
|
NM
|
ZE
|
PM
|
PB
|
PB
|
|
PS
|
NVB
|
NB
|
NS
|
PM
|
PB
|
PB
|
PVB
|
|
PM
|
NVB
|
ZE
|
PM
|
PB
|
PB
|
PVB
|
PVB
|
|
PB
|
NVB
|
ZE
|
PM
|
PB
|
PVB
|
PVB
|
PVB
|
Figure (VI.20) Base des règles du régulateur II
Ici, la méthode pour déterminer les
règles est appelée en anglais << bang-bang control
>> [44]. Ce type de méthode est utilisée pour amener
initialement le système près du point de fonctionnement
souhaité, puis changer la polarité de la variable de commande
afin d'éviter un dépassement. Ces deux étapes sont
visualisées par les régions A et B dans le tableau (VI-23) :
|
e
|
|
de
|
|
NB
|
NM
|
NS
|
ZE
|
PS
|
PM
|
PB
|
|
NB
|
|
|
|
|
|
|
|
|
NM
|
|
|
|
|
B
|
|
|
|
NS
|
|
|
|
|
|
|
|
|
ZE
|
|
|
|
D
|
|
|
A
|
|
PS
|
|
|
C
|
|
|
|
|
|
|
PM
|
|
|
|
|
|
|
|
|
|
PB
|
|
|
|
|
|
|
|
|
Figure (IV.21) Schéma de règles en principes de
<< bang-bangc control >>
Ce principe est répété dans la
région C, mais plus modestement. Les flèches décrivent le
chemin, qui est suivi dans le tableau (VI.21) en cas d'un échelon
positif comme signal de référence. Par conséquent, le
reste du tableau est rempli par symétrie à la région D.
VI.6 Application de la logique floue au modèle
réduit du schéma multi_enroulements de la machine
asynchrone
VI.6.1 Résultats de la simulation
le régulateur flou a été simulé
sous différentes conditions avec ou sans défauts rotorique ; les
résultats de simulation permettant ainsi de comparer les deux types de
régulations (classique et floue). Ces simulations s'avèrent
nécessaires dans le processus d'évaluation des régulateurs
à logique floue.
1. Machine saine
a. Machine saine à vide
Dans une première étape, nous avons simulé
le fonctionnement du régulateur flou avec une machine saine à
vide. Ce dernier présente un grand intérêt pour une
implémentation en temps réel au niveau algorithmique (meilleure
utilisation de la mémoire et temps de traitement plus rapide ).
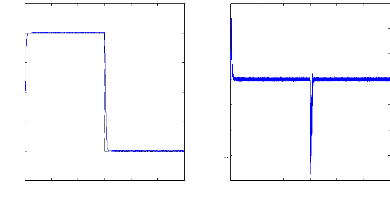
La figure (VI.22) montre la réponse de la vitesse et du
couple avec un régulateur de vitesse flou dans le cas d'une machine
à vide. Les temps de réponse en démarrage sont
respectivement de 0.2s pour une consigne de 1000 tr/mn . Les temps d'inversion
de la vitesse à -1000 tr/mn et 1000 tr/mn sont de l'ordre de 0.4s. Les
temps de réponse et d'inversion sont pratiquement identiques à
ceux du régulateur classique.
1500
1000
500
0
n (trim n)
-500
-1000
-1500
60
40
20
0
-20
C en (N .m )
-40
-60
-80
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
Figure (VI.22) : vitesse de rotation, couple
électromagnétique , simulation avec modèle,
machine
saine à vide.
0 0.5 1 1.5 2 2.5 3
t(s)
1 1.02 1.04 1.06 1.08 1.1 1.12
t(s)
jas(A )
-10
-20
-30
40
30
20
10
0
-1
-2
-3
-4
-5
5
4
3
2
1
0
zoom
jas(A )
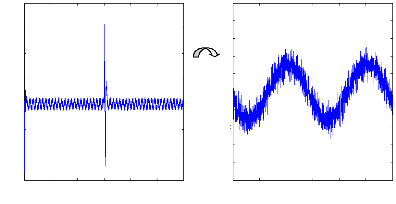
Figure (VI.23) : courant statorique, simulation avec
modèle réduit, machine
Saine à vide .
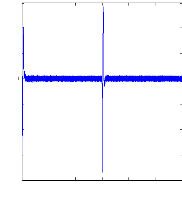
0 0.5 1 1.5 2 2.5 3
t(s)
irbo(A )
-1000
-1500
-2000
1500
1000
-500
500
0
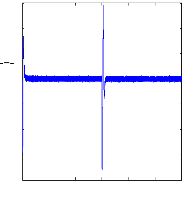
0 0.5 1 1.5 2 2.5 3
t(s)
irbilA
-1000
-1500
-2000
1500
1000
-500
500
0
Figure (VI.24) : courants dans les barres rotoriques : Irb0,
Irb1,
simulation avec modèle global, machine saine à
vide
b. Machine saine en charge
Les résultats de simulation de la figure (VI.25) montrent
que l'allure de la courbe de vitesse est similaire à celle obtenue par
un (PI classique) mais avec un temps de montée un peu plus rapide
(environ 0.17 s) ceci est dû au fait que les domaines physiques relatifs
à l'erreur et la variation de l'erreur soient plus larges dans le cas du
contrôleur flou. Le comportement des autres grandeurs est similaire
à celui obtenu avec un régulateur conventionnel. Les
réponses des systèmes sont caractérisées par les
même faits : le démarrage et l'inversion de vitesse s'effectuent
à couple maximal .
La figure (VI.25) montre également l'effet d'une
perturbation du couple de charge en régime permanent Cr=3.5N.m. Le
contrôleur flou reste pratiquement insensible à cette variation du
couple résistant. La réaction du régulateur à
logique floue au moment d'application de charge est aussi
caractérisée par une variation plus petite et un temps plus court
par rapport au régulateur classique.
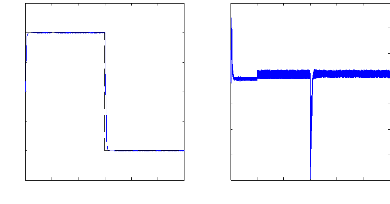
1500
1000
500
0
n (trim n )
-500
-1000
-1500
60
40
20
0
-20
C en (N .m )
-40
-60
-80
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
Figure (VI.25) : vitesse de rotation, couple
électromagnétique , simulation avec modèle,
machine
saine en charge Cr= 3.5 N.m
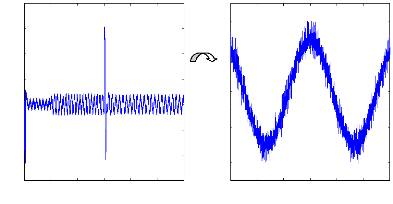
0 0.5 1 1.5 2 2.5 3
t(s)
1 1.02 1.04 1.06 1.08 1.1 1.12
t(s)
las (A )
-10
-20
-30
40
30
20
10
0
-1
-2
-3
-4
-5
5
4
3
2
0
1
zoom
las (A )
Figure (VI.26) :courant statorique, simulation avec
modèle réduit, machine
saine en charge, Cr=3.5N.m.
0 0.5 1 1.5 2 2.5 3
t(s )
irbo(A)
-1000
-1500
-2000
1500
1000
-500
500
0
0 0.5 1 1.5 2 2.5 3
t(s)
irb 1 (A )
-1000
-1500
-2 00 0
1500
1000
-500
500
0
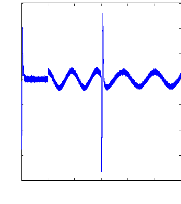
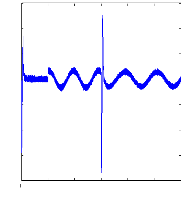
Figure (VI.27) : courants dans les barres rotoriques : Irb0,
Irb1, simulation avec modèle global,
machine saine en charge,
Cr= 3.5 N.m
2. Machine en défaut
a. Machine avec cassure de barre
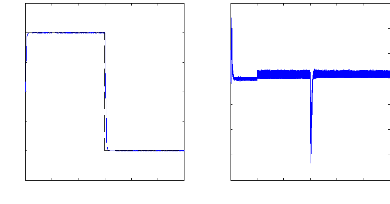
La figure (VI.28) illustre l'évolution temporelle en
régime transitoire et en régime permanent de la vitesse de
rotation, on a une inversion de vitesse à t=0.4s. La figure illustre
aussi du couple électromagnétique Cem en
présence d'une rupture des barres rb0 à t=1s.
Aprés une phase transitoire, celui-ci répond
instantanément et suit la référence sans
dépassement ni erreur statique Cr=3.5 N.m a cause de la
structure du régulateur flou, les réponses des systèmes
sont caractérisées par les même faits :
la vitesse de référence est atteinte en 0,15 sec
environ lors de l'inversion de vitesse selon une rampe.
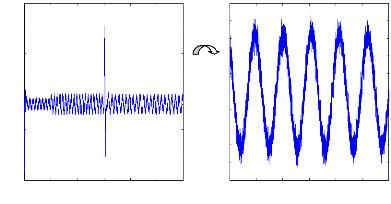
La figure (VI.29) illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique
en présence d'une rupture de barre rb0 à t=1s .
La figure (VI.30) illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1 en présence d'une rupture de barre
rb1 à t=1s,et on observe le courant dans la barre
rb0, qui proche de Zéro a cause de la cassure . Les courants
circulant dans les barres adjacentes aux barres cassées sont très
supérieurs a leur valeur nominale. On conclut donc qu'il y a un risque
de défaillances en chacune dans la mesure ou les contraintes
électriques et thermiques sont redistribuées sur les conducteurs
adjacents.
On remarque que la vitesse dans la figure (VI.28) est obtenue
comme dans le régulateur PI et que l'évolution du couple, des
courants est également identique.
Lorsque on a une cassure de barre la durée d 'inversion de
la vitesse est plus importante mais il n'existe plus de dépassement
comme dans le cas d'un régulateur linéaire.
La réaction des régulateurs à logique
floue au moment d'application de charge est aussi caractérisé par
une variation plus petite et un temps plus court par rapport aux
régulateurs classiques
1500
1000
500
0
n (trim n)
-500
-1000
-1500
60
40
20
0
-20
C en (N .m )
-40
-60
-80
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
Figure (VI.28) : vitesse de rotation, couple
électromagnétique, simulation avec le modèle
réduit,
machine en défaut et en charge : rupture d'une barre
à t=1s
0 0.5 1 1.5 2 2.5 3
t(s)
1 1.05 1.1 1.15 1.2 1.25 1.3
t(s)
las (A )
-10
-20
-30
40
30
20
10
0
-1
-2
-3
-4
-5
5
4
3
2
0
1
zoom
las (A )
Figure (VI.29) : courant statorique, machine en défaut,
en charge Cr= 3.5Nm
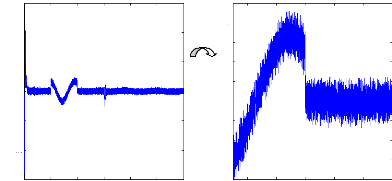
irb o (A )
-1000
-1500
1500
1000
-500
500
0
zoom
irb o (A )
-100
-150
-200
250
200
150
100
-50
50
0
0 0.5 1 1.5 2 2.5 3 0.8 0.9 1 1.1 1.2 1.3
t(s) t(s)
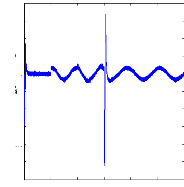
0 0.5 1 1.5 2 2.5 3
-
irb 1 (A )
-1000
-1500
-200 0
-250 0
-3000
2000
1500
1000
500
00
0
t(s )
Figure (VI.30) : Courants dans les barres rotoriques : Irb0,
Irb1, machine en
défaut, simulation avec modèle global,
rupture de la barre rb0 à t= 1s
b. Machine avec cassure de deux barres
La figure (VI.31) illustre l'évolution temporelle en
régime transitoire et en régime permanent du couple
électromagnétique Cem en présence d'une rupture
de barre rb0 a t=1s et rb1 a t=2s. Aprés une phase
transitoire, celui-ci répond instantanément et suit la
référence sans dépassement ni erreur statique
Cr=3.5 N.m a cause de la structure du régulateur flou, les
réponses des systèmes sont caractérisées par les
même faits :
la vitesse de référence est atteinte en 0,15 sec
environ lors de l'inversion de vitesse selon une rampe.
La figure (VI.32) illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique
en présence d'une rupture de barre rb0 à t=1s et
rb1 à t=2s .
La figure (VI.333) illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants de barres
Irb0 , Irb1, en présence d'une rupture de barre rb0 à t=1s et rb1
à t=2s. Les courants circulant dans les barres adjacentes aux barres
cassées sont très supérieurs a leur valeur nominale. On
conclut donc qu'il y a un risque de défaillances en chacune dans la
mesure ou les contraintes électriques et thermiques sont
redistribuées sur les conducteurs adjacents.
Les effets de la cassure de barre (oscillation de w et
Cem) croit rapidement avec le nombre de barres cassé ;
d'où on observe:
- Augmentation de l'amplitude des oscillations. La grande
amplitude des oscillations accélère la
détérioration de la machine.
- L'amplitude des courants des phases statoriques. est
proportionnelle au nombre de barres cassées.
- Lors des défauts rotoriques, les courants dans les
barres cassées chutent pratiquement à
zéro, tandis que
les courants dans les barres voisines deviennent
déséquilibrés. Les
courants qui conduisaient les barres
cassées se répartit alors dans les barres voisines
Lorsque on a une cassure de barre la durée d 'inversion
de la vitesse est plus importante
mais il n'existe plus de dépassement comme dans le cas
d'un régulateur linéaire.
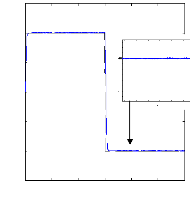
1500
1000
500
0
n (trim n )
-9 4 0
-960
-980
-1020
1 0 4 0
-
-1060
-1080
-1100
14 16 18 2 22 24
t(s
-500
-1000
-1500
0 0.5 1 1.5 2 2.5 3
t(s)
1 1 2 0
-1 1 4 0
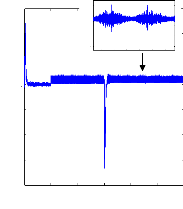
10
5
60
0
40
-5
0
2 1 2 2 2 3 2 4 2 5 2 6
t (s )
20
-40
-60
-80
0 0.5 1 1.5 2 2.5
t(s)
0
-20
C en (N .m )
Figure (VI.31) :vitesse de rotation, couple
électromagnétique et le courant
statorique, machine en charge
et en défaut : 2 barres cassées
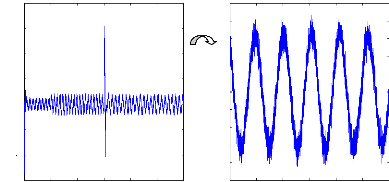
las (A )
-10
-30
40
30
20
20
10
zoom
las (A )
-1
-2
-3
-4
-5
5
4
3
2
0 0.5 1 1.5 2 2.5 3 1.05 1.1 1.15 1.2 1.25 1.3
t(s) t(s)
Figure (VI.32) :courant statorique, machine en charge et en
défauts, 2barres
cassées
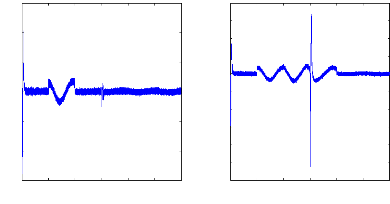
0 0.5 1 1.5 2 2.5 3
t(s)
!rbl )
-
-1000
-1500
-2000
-2500
-3000
2000
1500
1000
500
500
0 0.5 1 1.5 2 2.5 3
t(s)
irb o (A )
-1000
-1500
1500
1000
-500
500
Figure (VI.33) :courants dans les barres rotoriques : Irb0,
Irb1,Machine en charge et en défaut, simulation avec
modèle global : 1 barre cassée rb0 à t=1s, 2
barre cassée rb1 à t=2s
3. Variation de la charge
Pour 0.6s<t<3s, on applique un couple de charge de 3.5N.m
;
a l'instant t=2s, on applique un couple de charge
Cr=5.5N.m.
On constate également que les variations du couple de
charge n'ont aucune influence sur la réponse de la vitesse dans le cas
d'un régulateur flou (figure IV.34). Les figures (IV.34 à IV.35)
confirment aussi ces résultats.
On remarque que la vitesse est obtenue comme dans le
régulateur PI et que l'évolution du couple, des flux et des
courants est également identique. Les temps de réponse et
d'inversion de la vitesse sont respectivement égaux à 0.4 s et
0.45 s.
La réaction des régulateurs à logique
floue au moment d'application de charge est aussi caractérisé par
une variation plus petite et un temps plus court par rapport aux
régulateurs classiques
On constate également que ce correcteur offre une
réponse bien meilleure que celui du (PI ). Les dépassements et
les temps de réponse sont beaucoup plus faibles qu'avec un
régulateur classique.
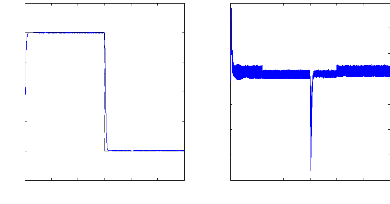
1500
1000
500
0
n (trim n )
-500
-1000
-1500
60
40
20
0
-20
C en (N .m )
-40
-60
-80
0 0.5 1 1.5 2 2.5 3
t(s)
0 0.5 1 1.5 2 2.5 3
t(s)
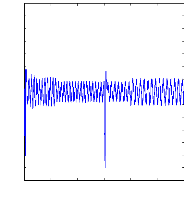
0 0.5 1 1.5 2 2.5 3
t(s )
las (A )
-10
-15
-20
-25
-30
-35
10
-5
5
0
35
30
25
20
15
Figure (VI.34) : vitesse de rotation, couple
électromagnétique,
variation de la charge.
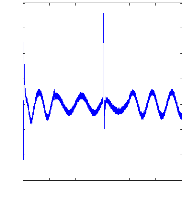
0 0.5 1 1.5 2 2.5 3
t(s)
irbo(A)
-1000
-1500
2000
1500
1000
-500
500
0
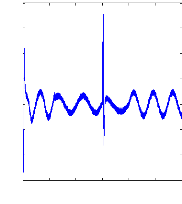
0 0.5 1 1.5 2 2.5 3
t(s)
irb 1 (A )
-1000
-1500
2000
1500
1000
-500
500
0
Figure (VI.36) : courants dans les barres rotoriques, Irb0,
Irb1
machine avec variation de charge, simulation avec modèle
global.
| 


