VI.3.1 Implication floue
L'implication floue donne une information sur le degré
de vérité d'une règle floue. En d'autre termes, on
quantifie la force de véracité entre la prémisse et la
conclusion. Considérons par exemple les deux propositions floues.
? x est A ?
? y est B ? Où x et y sont des variables floues et A et B
des ensembles flous de l'univers du discours U.
Ainsi que la règle floue : Si ? x est A ?
Alors ? y est B ? .
L'implication floue donne alors le degré de
vérité de la règle floue précédente à
partir des degrés d'appartenance de x à A (prémisse) et de
y à B (conclusion).
On notera implication : opérateur imp (équivalent
à l'opérateur Alors). Les normes d'implication les plus
utilisées sont :
imp(uA(x), uB(y)) = min(uA(x), uB(y)) (VI.5)
- La norme Larsen imp(uA(x), uB(y)) = (uA(x).uB(y))
(VI.6)
VI.3.2 Inférence floue
Le problème tel qu'il se pose en pratique n'est
généralement pas de mesurer le degré de
véracité d'une implication mais bien de déduire, à
l'aide de faits et de diverses règles implicatives, des
évènements potentiels. En logique classique, un tel raisonnement
porte le nom de Modus Ponens (raisonnement par l'affirmation).
Si p q vrai
- La norme Mamdani
Alors q vrai
et p vrai
De façon générale, les conditions
d'utilisation du Modus Ponens Généralisé sont les
suivantes :
Prémisse conclusion
Règle floue : Si x est A Alors y est B
Fait observé : Si x est A'
Conséquence : y est B'
A' et B' sont les ensembles flous constatés dans le cas
que l'on traite et ne sont pas nécessairement strictement égaux
à A et B. B' est l'ensemble flou résultant de A' par
l'application de l'implication.
Les informations disponibles pour déterminer la
conséquence sont donc d'une part celles relatives à la
règles, quantifiées par l'implication floue uB/A(x,
y), d'autres part celles relatives au fait observé, quantifiées
par la fonction d'appartenance uA'.
-Par matrice d'inférence
Elle rassemble toutes les règles d'inférences
sous forme de tableau. Dans le cas d'un tableau à deux dimension, les
entrées du tableau représentent les ensembles flous des variables
d'entrées (température : T et vitesse : V). L'intersection d'une
colonne et d'une ligne donne l'ensemble flou de la variable de sortie
définie par la règle. Il y a autant de cases que de
règles.
|
U
|
T
|
|
F
|
M
|
E
|
|
V
|
F
|
Z
|
P
|
GP
|
|
E
|
Z
|
Z
|
P
|
Les règles que décrit ce tableau sont (sous forme
symbolique) :
Si T est F Et V est F
Alors U = Z Ou
Si T est M Et V est F
Alors U = P Ou
Si T est E Et V est F
Alors U = GP Ou
Si T est F Et V est E
Alors U = Z Ou
Si T est M Et V est E
Alors U = Z Ou
Si T est E Et V est E
Alors U = P
Dans l'exemple ci-dessus, on a représenté les
règles qui sont activées à un instant donné par des
cases sombres :
Si (T est M Et V est F)
Alors U = P Ou
Si (T est E Et V est F)
Alors U = GP
Il s'agit maintenant de définir les degrés
d'appartenance de la variable de sortie à ses sous-ensembles flous. Nous
allons présenter les méthodes d'inférence qui permettent
d'y arriver. Ces méthodes se différencient essentiellement par la
manière dont vont être réalisée les
opérateurs (ici "Et " et "Ou") utilisés dans
les règles d'inférence.
Les trois méthodes d'inférence les plus usuelles
sont : Max-min, Max-produit et Somme-produit VI.3.3 Agrégation
des règles
Lorsque la base de connaissance comporte plusieurs
règles, l'ensemble flou inféré B' est obtenu après
une opération appelée agrégation des règles. En
d'autres termes l'agrégation des règles utilise la contribution
de toutes les règles activées pour en déduire une action
de commande floue. Généralement, les règles sont
activées en parallèle et son liées par l'opérateur
" Ou ".
Nous pouvons considérer que chaque règle donne un
avis sur la valeur à attribuer au signal de commande, le poids de chaque
avis dépend du degré de vérité de la conclusion.
VI.4 Conception d'un contrôleur flou
Après avoir énoncé les concepts de base et
les termes linguistiques utilisés en logique floue, nous
présentons la structure d'un contrôleur flou.
En général, un contrôleur flou est un
système qui associe à tout vecteur d'entrée
X=[x1,x2,...,xn] un vecteur de sortie Y=[y1,y2,....yn] tel que Y=F(X) où
F(X) est souvent une fonction non linéaire.
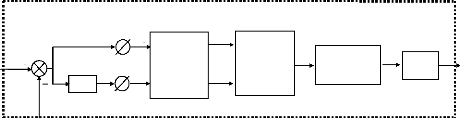
Le schéma de base d'un contrôleur flou repose sur
la structure d'un régulateur classique à la différence que
l'on va retenir la forme incrémentale. Cette dernière donne en
sortie, non pas la grandeur de commande à appliquer au processus mais
plutôt l'incrément de cette grandeur.
Contrôleur Flou
Iref
+
1 -
-z
1
e
de Kde
Ke
Fuzzification
de~
e~
Base de Règles et logique prise de décision
dRs
Défuzzification
dRs~
?
RS
Courant mesuré
Figure (VI.4) : Structure interne d'un contrôleur flou
Dans le schéma ci-dessus comme dans ce qui suit, nous
notons
· e : l'erreur, elle est définie par la
différence entre la consigne et la grandeur à réguler.
e ( k ) = e* (k ) -
e(k ) (VI.7)
· de: la dérivée de l'erreur, elle est
approchée par
de k ( ) ( 1)
e k e k
- -
( ) = (VI.8)
Te
La sortie du régulateur est donnée par
R S ( k ) = R S
(k -1) +dR S (k) (VI.9)
Des facteurs d'échelle des gains sont utilisés en
entrée et en sortie du contrôleur flou, ils permettent de changer
la sensibilité du régulateur flou sans en changer sa
structure.
Les règles d'inférences permettent de
déterminer le comportement du contrôleur flou. Iidoit
donc inclure des étapes intermédiaires qui lui permettent de
passer des grandeurs réelles
vers les grandeurs floues et vice versa; ce sont les
étapes de fuzzification et de defuzzification (figure VI.5)
1- L'interface de fuzzification inclut les fonctions
suivantes :
Les ensembles flous des variables d'entrée et leurs
fonctions d'appartenance sont à définir en premier lieu.
L'étape de fuzzifiation permet de fournir les
degrés d'appartenance de la variable floue à ses ensembles flous
en fonction de la valeur réelle de la variable d'entrée.
2- La base de connaissance comprend une connaissance du domaine
d'application et les buts du contrôle prévu. Elle est
composée.
- d'une base de données fournissant les
définitions utilisées pour définir les règles de
contrôle linguistique et la manipulation des données
floues dans le contrôleur ;
- d'une base de règles caractérisant les buts et
la politique de contrôle des experts du
domaine au moyen d'un ensemble de règles de contrôle
linguistique.
Comme nous l'avons précédemment
évoqué, nous allons nous baser sur une matrice ou table
d'inférence pour cette étape.
La construction d'une telle table d'inférence repose sur
une analyse qualitative du processus.
L'inférence se fait donc sur la base des matrices que
l'on vient de décrire. On commence par utiliser un opérateur pour
définir la description symbolique associée à la
prémisse de la règle ; c'est à dire réaliser le "
Et ". On passe ensuite à l'inférence proprement dire qui
consiste à caractériser la variable floue de sortie pour chaque
règle. C'est l'étape de la conclusion " Alors ".
Enfin, la dernière étape de l'inférence,
appelée agrégation des règles, permet de
synthétiser ces résultats intermédiaires.
Comme nous l'avons vu, la manière de réaliser les
opérateurs va donner lieu à des contrôleurs flous
différents. Les régulateurs les plus courants sont ceux de :
· Régulateur type Mamdani
· Régulateur type Sugeno
Ils sont dits de type procédural . En effet, seule la
prémisse est symbolique. La conclusion, qui correspond à la
commande, est directement une constante réelle ou une expression
polynomiale fonction des entrées.
L'établissement des règle d'inférence est
généralement basé sur un des points suivants :
· l'expérience de l'opérateur et/ou du
savoir-faire de l'ingénieur en régulation et contrôle.
· Un modèle flou du processus pour lequel on
souhaite synthétiser le régulateur.
· Les actions de l'opérateur ; s'il n'arrive pas
à exprimer linguistiquement les régles qu'il utiliser
implicitement.
· L'apprentissage ; c'est dire que la synthèse de
règle se fait par un procédé automatique également
appelé superviseur. Souvent, des réseaux neuronaux y sont
associées.
L'évaluation des règles d'inférence
étant une opération déterministe, il est tout à
fait envisageable de mettre sous forme de tableau ce contrôleur.
Il reste, toutefois, intéressant dans certains
systèmes complexes, de garder l'approche linguistique plutôt que
d'avoir à faire à un nombre trop important de valeurs
précises .
De plus, un algorithme linguistique peut être
examiné et discuté directement par quelqu'un qui n'est pas
l'opérateur mais qui possède de l'expérience sur le
comportement du système.
La formulation linguistique de la sortie permet également
d'utiliser le régulateur flou en boucle ouverte donnant ainsi à
l'opérateur les consignes à adopter.
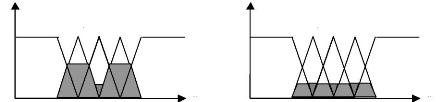
Si, après inférence, on se retrouve avec un
ensemble flou de sortie caractérisé par l'apparition de plus d'un
maximum, cela révèle l'existence d'au moins deux règles
contradictoires. Une grande zone plate (figure VI.7,8), moins grave de
conséquence, indiquerait que les règles, dans leur ensemble, sont
faibles et mal formulées.
u
u
N
Z P PG
NG
1
N
1
Z P PG
dRn
dRn
NG
Figure (VI.5) : Cas de régles floues Figure (VI.6) : Cas
de régles floues
contradictoires mal formulées
3- La logique de prise de décision est le noyau du
contrôleur flou, elle est capable de simuler la prise de décision
de l'être humain en se basant sur les concepts flous et les règles
d'inférences en logique floue.
4- L'inférence de défuzzification réalise
les fonctions suivantes :
- une cartographie d'échelle convertissant la plage des
variables de sortie aux univers de discours appropriés ;
- Une défuzzification fournissant une action de
contrôle (physique) à partir d'une action de contrôle
flou.
Pour pouvoir définir la loi de commande, le
contrôleur flou doit être accompagné d'une procédure
de défuzzification jouant le rôle de convertisseur de la commande
floue en valeur physique nécessaire pour un tel état du
processus. Il s'agit de calculer, à partir des degrés
d'appartenance à tous les ensembles flous de la variable de sortie,
l'abscisse qui correspond à la valeur de cette sortie.
Plusieurs stratégies de défuzzification existent,
les plus utilisées sont .
- Méthode du maximum
- Méthode de la moyenne des maxima
- Méthode du centre de gravité
- Méthode des hauteurs pondérées
| 


