V.3.4 Mesures
Le vecteur des mesures h(k) = [ids( k) iqs(k)] est
obtenu à partir des mesures des courants de ligne.
V.4 Application du filtre de Kalman Etendu a la machine
asynchrone
L'algorithme décrit ci-dessus est appliqué a
l'étude par simulation de l'estimation des paramètres d'une
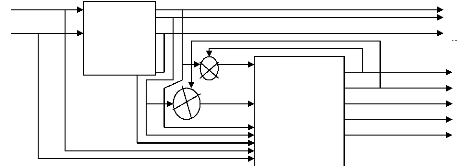
machine asynchrone. Le schéma de la configuration du système est
sur la figure (V.2).
Vqs
Vds
réduit
Modèle de la M.AS
Filtre
De
Kalman
Etendu
Ids
Iqs
ù
Îds
Îqs
Îdr
Îqr
S1
Figure (V.2) : schéma de configuration du modèle
pour l'estimation
V.5 Résultats de simulation
V.5.1 Suivi des courants
a- Machine Saine à vide
La simulation est faite pour un temps de 1.5s.
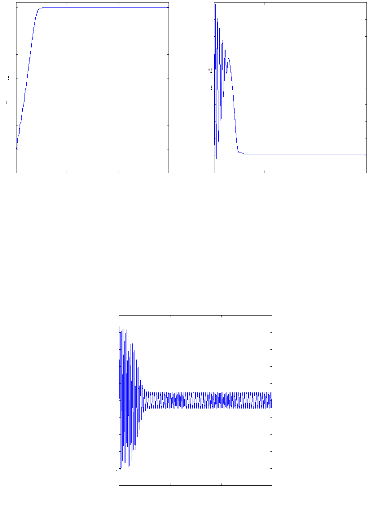
La figure (V.3) présente la variation de la vitesse, le
couple en absence du couple de charge. La figure (V.4) illustre le courant
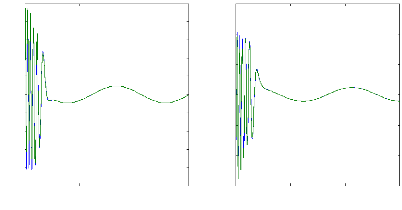
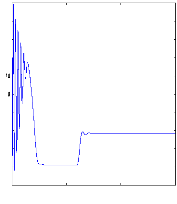
statorique en absence de la charge. La figure (V.5) montre la convergence des
courants estimés vers les courants réels pour les courants. Les
valeurs des courants se stabilisent à des valeurs proches de
zéro, a cause de l'absence du couple de charge.
las(A)
0
0 0.5 1 1.5
t(s)
1
1
Q (trim rtJ
3000
2500
2000
-500
000
500
00
0
0 0.5 1 1.5
t(s)
1
Cem(N.rn)
18
16
14
12
-2
6
4
2
0
Figure (V.3) : la vitesse de rotation, le couple ,
machine
saine à vide
25
20
15
10
5
-5
-10
-15
-2 0
0 0.5 t(s) 1 1.5
Figure (V.4 ) : courant statorique, machine saine à
vide
-25
0 0.5 1 1.5
t(s )
0 0.5 1 1.5
t(s )
25
20
15
10
5
0
-5
-10
id s sE s e (A )
-15
-20
-25
30
20
10
0
10
iqs!iqS E stim )
-
-20
-30
3000
2500
2000
00
(trim n_
000
500
0
-500
0 0.5 1 1.5
t(s)
0 0.5 1 1.5
t(s)
Cem(N.rn)
18
16
14
12
-2
6
4
2
0
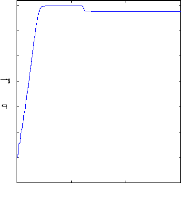
Figure (V.5) : courants et courants estimés:
ids et
Ids_estimé, iqs et
iqs_estimé, machine saine à vide
b- Machine saine en charge
On simule maintenant avec un couple de charge de 3.5N.m, alors la
machine opère en charge.
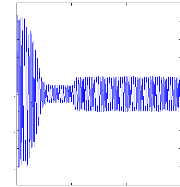
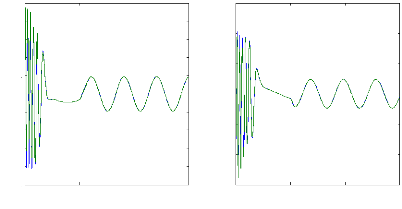
On voit, d'après la figures (V.8), La comparaison du
courant mesuré et estimé montre la bonne convergence du
filtre.
las (A
-1 0
-1 5
-2 0
-2 5
2 5
2 0
1 5
1 0
-5
5
0
0 0 .5 1 1 .5
t(s )
Figure (V.7) : courant statorique, machine saine en charge
Cr=3.5 N.m
0 0 .5 1 1 .5
t(s )
0 0.5 1 1.5
t(s)
2 5
2 0
1 5
1 0
5
0
-5
-1 0
ids sE stim e (A)
-1 5
-2 0
-2 5
3 0
2 0
1 0
0
1 0
-
iqs!iqSE stim a )
-20
-30
Figure (V.8) : courants et courants estimés : ids
et
Ids_estimé, iqs et iqs_estimé,
machine saine en charge
0 0.5 1 1.5 2 2.5 3
t(s)
1
n(trLm n)
3500
3000
2500
2000
1000
-500
500
500
0
0 0.5 1 1.5 2 2.5 3
t(s)
1
Cem(N.rn)
20
15
-5
5
0
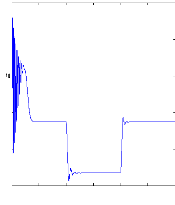
Figure (V.9) : vitesse, le couple et le courant statorique,
machine saine lors
d'une variation de charge.
0 0.5 1 1.5 2 2.5 3
t(s)
las(A)
-2 0
-25
-10
-15
25
20
15
10
-5
5
0
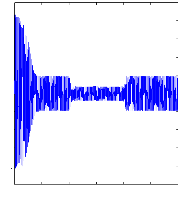
Figure (V.10) : courant statorique lors de variation de charge
0 0.5 1 1.5 2 2.5 3
t(s)
-
iqs!iqS E stim )
-20
-30
3 0
2 0
1 0
1 0
0
0 0.5 1 1.5 2 2.5 3
t(s)
id sE stim e (A)
-10
-15
-20
-25
25
20
15
10
-5
5
0
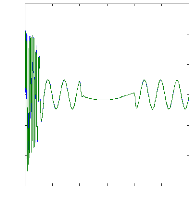
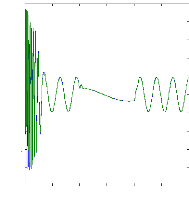
Figure (V.11) : courants et courants estimés:
ids et
Ids_estimé, iqs et
iqs_estimé,lors de variation de la charge
c- Machine avec défaut
1. cas d'une cassure de barre
Vu la difficulté de voir les défaut à vide,
on va simuler la machine en charge avec cassure de barre.
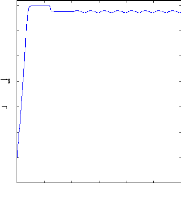
La figure (V.12) illustre l'évolution temporelle en
régime transitoire et en régime permanent de la vitesse de
rotation, celle-ci se stabilise a une valeur de 2219 tr/mn. La figure illustre
aussi du couple électromagnétique Cem en présence d'une
rupture des barres rb0 à t=1s. Aprés une phase
transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de
la présence du couple de charge.
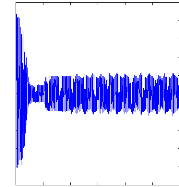
La figure (V.13) illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique
en présence d'une rupture de barre rb0 à t=1s .
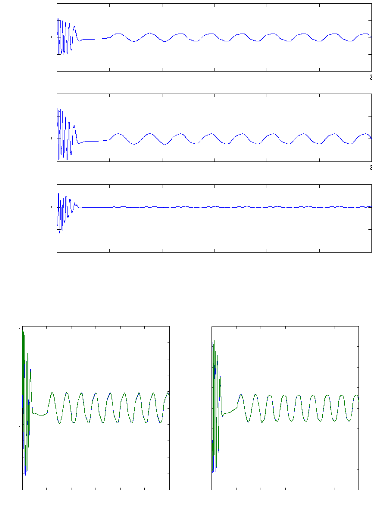
La figure (V.15) illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants
ids , idr, avec leurs courant estimés en
présence d'une rupture de barre rb0 à t=1s. Les
courants circulant dans les barres adjacentes aux barres cassées sont
très supérieurs a leur valeur nominale. La comparaison du courant
mesuré et estimé montre la bonne convergence du filtre.
0 0.5 1 1.5 2 2.5 3
t(s)
1
1
R (trim n_
3000
2500
2000
-500
000
500
00
0
0 0.5 1 1.5 2 2.5 3
t(s)
1
Cem(N.rn)
18
16
14
12
-2
6
4
2
0
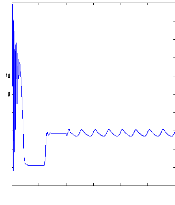
Figure (V.12) : vitesse de rotation, couple
électromagnétique,
simulation avec le modèle
réduit, machine en défaut en charge, Cr=3.5 N.m
las(A)
-2 0
-25
-10
-15
25
20
15
10
-5
5
0
0 0.5 1 1.5 2 2.5 3
t(s )
Figure (V.13) : courants statorique, avec cassure
d'une barre rb0
4 0
2 0
0
ids(A)
-2 0
-4 0
0 0 .5 1
t(s ) 1 .5
2 2 .5
0 0 .5
1
1 . 5
t(s )
2 2 .5
t(s)
t(s)
rotor sn
1 barre cassée
0 0 .5 1 1 .5 2 2 .5 3
t(s )
Figure( V.14) :Courant ids et
ids-estimé avec cassure d'une barre rb0 et l'erreur
id sE stim e
-2 0
4 0
2 0
0
1 0
0
-1 0
-2 0
e rre u r(A )
0 0.5 1 1.5 2 2.5 3
0 0.5 1 1.5 2 2.5 3
25
20
15
10
5
0
-5
-10
ids iidsE slim OA )
-15
-20
-25
4000
3000
2000
000
0
000
-2000
1
-1
id r' ill. rE s fin' elA )
-3000
-4000
Figure (V.15) : courants et courants estimés dans les
barres rotoriques : ids et
Ids_estimé, idr et
idr_estimé, avec cassure de barre rb0
2. Cas d'une cassure de deux barres
On impose maintenant un couple de charge de 3.5 N.m à
t=0.5s et la machine opère alors en charge avec cassure de deux
barres.
La figure (V.16) illustre l'évolution temporelle en
régime transitoire et en régime permanent du couple
électromagnétique Cem en présence d'une rupture
de barre rb0 a t=1s et rb1 a t=2s. Aprés une phase
transitoire, celui-ci se stabilise a une valeur proche de 3.5 N. m a cause de
la présence du couple de charge, on remarque dans cette figure des
ondulations dans les allures de la vitesse et du couple, a cause des cassures
des barres.
La figure (V.17) illustre l'évolution temporelle en
régime transitoire et en régime permanent du courant statorique ,
en présence d'une rupture de barre rb0 à t=1s.
La figure (V.18) illustre l'évolution temporelle en
régime transitoire et en régime permanent des courants
ids , idr et leurs courants estimés en
présence d'une rupture de barre rb0 à t=1s et
rb1 à t=2s, ou on remarque la convergence du filtre. Les
courants circulant dans les barres adjacentes aux barres cassées sont
très supérieurs a leur valeur nominale. On conclut donc qu'il y a
un risque de défaillances en chacune dans la mesure ou les contraintes
électriques et thermiques
sont redistribuées sur les conducteurs adjacents.
0 0.5 1 1.5 2 2.5 3
t(s)
1
1
R (trim n_
3000
2500
2000
-500
000
500
00
0
0 0.5 1 1.5 2 2.5 3
t(s)
1
Cem(N.rn)
18
16
14
12
-2
6
4
2
0
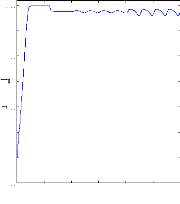
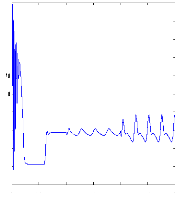
Figure (V.16) : vitesse de rotation, couple
électromagnétique, simulation avec le
modèle
réduit, machine en défaut en charge,
Cr=3.5 N.m
las (A
-10
-15
25
20
15
10
20
25
-5
5
0
0 0.5 1 t(s) 1.5 2 2.5 3
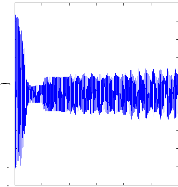
Figure (V.17) : courants statorique , avec cassure de deux
barres
!dr,-i_drE stim(A )
1
-2000
-3000
-4000
4000
3000
2000
000
000
0
25
20
15
10
5
0
-5
-10
ids s E stim e (A)
-15
-20
-25
0 0.5 1 1.5 2 2.5 3
t(s 0 0.5 1
t (s )1.5 2 2.5 3
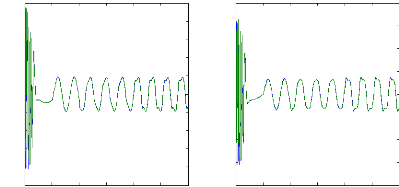
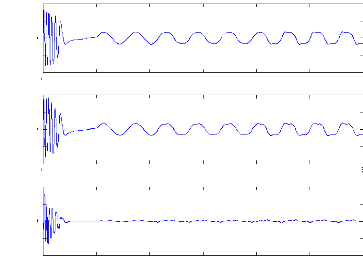
Figure (V.18) : courants et courants estimés dans : ids
et ids_estimé, idr et idr_estimé, avec cassure de
barre
rb0 et rb1
4 0 0 0
2 0 0 0
0
-2 0 0 0
-4 0 0 0
0 0 .5 1
1 . 5
t(s )
2 2 .5 3
4 0 0 0
2 0 0 0
0
-2 0 0 0
-4 0 0 0
0 0 .5 1
t(s )
1 .5 2 2 .5
id re s tim e
id r(A )
erre u r(A )
2 0 0 0
1 0 0 0
0
-1 0 0 0
-2 0 0 0
0 0 .5 1 1 . 5 2 2 .5
t(s )
0 .5 1 1 . 5 2
t(s )
2 .5
0 .5 1 1 . 5 2
t(s )
2 .5
0 0 .5 1 1 .5 2 2 .5 3
t(s )
ids(A)
-2 0
-4 0
4 0
2 0
0
id sestim e
-2 0
4 0
2 0
0
e rre u r(A )
-1 0
-2 0
1 0
0
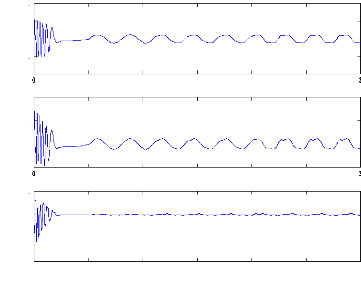
Figure (V.19) : Courant idr et
idr-estimé avec cassure de deux barre
> La cassure d'une barre
Nous simulons la rupture de la première barre (k=0) donc
Rb cassé = 11*Rb sain
Les valeurs de S1, S2, S3 et S4 deviennent :-
S1= 3.29213.10-5 S2= 5.45625.10-6 S3=
5.45625.10-6 S4= 3.29213.10-5
> La cassure de deux barres
On simule la rupture de deux barres adjacentes (K=0, K=1)
Les valeurs de S1, S2, S3 et S4 deviennent :-
S1= 4.11738.10-5 S2= 1.86375.10-5 S3=
1.86375.10-5 S4= 4.11738.10-5
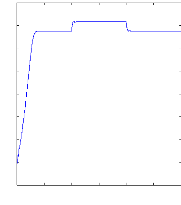
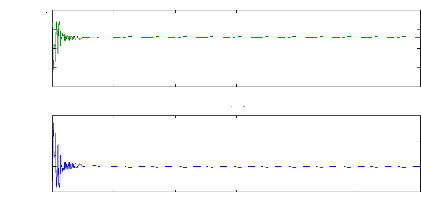
a. Machine saine à vide : La figure
(V.21) présente la variation de la résistance équivalente
rotorique estimée.
t ( s )
6 x 1 0 - 5
4
2
0
-2
0 0 .5 1 1 .5 2 2 .5 3
StSlestime
(Ohm)
erreur(Ohm)
-2
4 x 1 0 - 5
2
0
0 0 .5 1 1 .5 2 2 .5 3
t ( s )
Figure (V.21) :Estimation de la résistance rotorique
équivalente S1, machine à vide
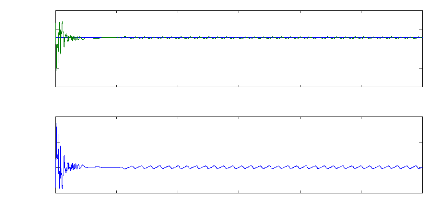
b. Machine saine en charge :
StSlestime
(Ohm)
erreur(Ohm)
0 0 .5 1 1 .5 2 2 .5 3
-2
6 x 1 0 - 5
4
2
0
0 0 .5 1 t ( s 1 .5 2 2 .5 3 )
1 0 - 5
4
2
0
-2
t ( s )
Figure (V.22) : mode la résistance rotorique
équivalente S1, machine saine en charge Cr=3.5N.m
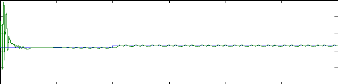
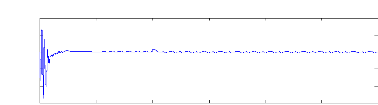
c- Machine avec une cassure de barre :
x 10-5
Rotor sain
0 0.5 1 1.5 2 2.5
|
,S (Q)
1 Estime
S
1
|
6 5 4 3 2
1
|
1 barre cassée
0 0.5 1 1.5 2 2.5
t(s )
Erreur(Q)
-1
-2
-3
2
0
1
x 10-5
t(s )
Figure (V.23) : Estimation de la résistance rotorique
équivalente S1, machine en défaut (cassure
d'une barre) et en
Charge Cr=3.5N.m
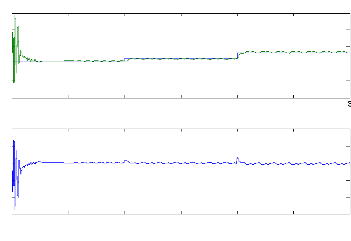
d-Cas d'une cassure de deux barres :
,S (Q)
1 Estime
S
I
Erreur(Q)
Rotor sain
1 barre cassé
2iéme barre cassée
0 0.5 1 1.5 2 2.5
x 1 0 -5
6
x 1 0 -5
2
t(s )
1
0
-1
-2
-3
0 0.5 1 1.5 2 2.5 3
t(s )
5
4
3
2
1
Figure (V.24) : Estimation de la résistance rotorique
équivalente S1, machine en défaut
(cassure de deux barres) et
en Charge Cr=3.5N.m
Les figures précédentes présentent la
résistance équivalente des barres rotoriques observés.
Après une période de convergence, la résistance
observée converge vers la même résistance. Nous remarquons
une légère oscillation autour de cette valeur.
V.6 Variation des parametres :
En pratique, les paramètres de la machine asynchrone,
autres que S1, ne sont pas connus exactement et leur estimation
résulte d'une identification du système effectuée, par
exemple,
par des méthodes d'estimation hors-ligne.
Ces paramètres sont nécessaires pour le calcul du
modèle discret de la machine utilisé par le filtre de Kalman. En
outre, les paramètres de la machine asynchrone peuvent changer en raison
des phénomènes physiques :
échauffement, saturation magnétique, . . ., . Deux
problèmes se posent alors dans le calcul du filtre de Kalman :
- La variation des paramètres physiques de la machine
asynchrone (comportement non-stationaire),
- L'incertitude paramétrique dans le modèle discret
due a l'erreur lors de l'identification préalable
V.7 Conclusions :
Nous avons décrit une technique pour estimer et suivre
les courants et la résistance rotorique équivalente des barres
rotoriques du modèle réduit du schéma multi-enroulements
de la machine asynchrone. Cette technique a été
vérifiée par simulation. Les résultats obtenus montrent
que le filtre de Kalman étendu peut estimer avec précision en
opération normale de la machine, et en présence des
défauts rotoriques ( barres cassées).
L'avantage d'utiliser les courant statoriques comme variables
d'état est qu'ils sont directement mesurables. La simulation avec le
logiciel MATLAB à donner des résultats , qui reflètent
l'état de la machine. Notre filtre nous permet d'identifier la
présence d'un défaut au niveau du rotor. Nous pouvons ainsi
distinguer le défaut physique qui modifient le fonctionnement du
moteur.
| 


