Estimation des paramètres et des états de la machine asynchrone en vue du diagnostic des défauts rotoriques

Chapitre v

Estimation des paramètres de la

machine asynchrone par le filtre de

Kalman Etendu en vu de détection des

défauts rotoriques

V.1 Introduction

Le diagnostic de défaut des machines électriques gagne l'importance particulière en raison des pertes de temps d'arrêt et de revenu de machine à l'industrie. Souvent, ces machines courent les charges critiques et leur panne soudaine peut être catastrophique. Ainsi, le système d'entraînement du moteur devrait également avoir les dispositifs diagnostiques pour prévoir des défauts de machine à leur commencement même. En conséquence, il devient très important d'avoir des modèles de machine et de commander les techniques qui peuvent distinguer l'état sain et défectueux des machines. [26]

Dans le domaine de l'estimation des paramètres des machines électriques a courants alternatifs, beaucoup des méthodes ont été proposées. Selon les considérations sur les différentes perturbations, ces méthodes peuvent être déterministes ou stochastiques. Les premières ne font pas d'hypothèse sur les propriétés des bruits, tandis que les secondes tiennent compte des bruits de perturbation du système.

Parmi Les méthodes stochastiques, nous avons, le filtrage de Kalman. Un cas particulier de cette méthode est le Filtre de Kalman Etendu. Il est approprie pour le traitement des mesures bruitées discrètes et pour obtenir des estimes précis des variables d'état et des paramètres du modèle. La façon générale dont il le fait consiste a utiliser les facteurs suivants :

-Une connaissance de la dynamique du système et des mesures.

-La description statistique des bruits du système, des perturbations, des erreurs de mesure et des incertitudes du modèle du système.

- Une information sur les conditions initiales des variables d'intérêt.

Afin d'évaluer ce type de méthode sur un exemple simple représentatif, nous présentons dans ce chapitre, l'algorithme d'estimation en ligne basé sur le filtre de Kalman étendu, pour l'estimation des paramètres de la machine asynchrone en vu de détection des défauts rotoriques.

L'algorithme est vérifie par simulation. On considère une machine asynchrone avec son modèle multi-enroulements. Les variables mesurables sont les courants de phase, les tensions de phase et la vitesse du rotor.

V.2 Modèle discret de la machine asynchrone

L'estimation des variables d'état pour la détection des défauts a besoin d'un modèle dynamique multi-enroulements adéquat de la machine asynchrone. Le modèle réduit est obtenu en utilisant la transformation de PARK. Ce modèle pose les hypothèses habituelles décrites au chapitre II.

Le filtre de Kalman nécessite un modèle discret de la machine qui se déduit du modèle continu.

La représentation de la dynamique de la machine, avec un repère lie au rotor, est donnée par les équations suivantes :

dÖ _ds

VR . I

= + ù . ö

ds s qs (V.1)

s ds dt

-

dÖ _qs

V R . I

= + ù . ö

qs s ds (V.2)

s qs dt -

dödr

0 = . +

R I (V.3)

r dr dt

d ö qr

0 = . +

R I (V.4)

dt

r qr

En choisissant _ids, i_qs, id_r, i_qr,Ie comme variables d'état du modèle réduit du shéma multienroulements de la machine asynchrone, la représentation en espace d'état est :

x& = A . x ( t ) + B .u ( t )

( ) = ( ) ( ) ( ) ( ) ( )

[ ] ^T

x t _ids ^t _iqs ^t _idr ^t _iqr t i_e t

(V.5)

(V.6)

u ( t ) = [ Vds Vqs 0 0]^T (V.⁷)

Le courants stator, étant choisis comme mesures pour compléter le modèle d'espace d'état, l'équation de sortie est :

z ( t ) = h[ x (t ), t] (V.8)

Oil : h = [ ids iqs] (V.⁹)

Le modèle déterministe devient :

a14

-a 11 a12 .w - a13S1 -

0 0

0 0

a₃

S 1 a4

- a₆ . w - a₇ a 8 a₉ . S₁

a16 . w a₁₇ - a 18 - a₁₉ . S₁

? ?

?i

? ?

?i
Le ? ?
ÿ ? I e ÿ

0

0 Ò

?

0 Ò

?

0 Ò

?

? ? i ds

qs Ò

? i Ò

dr

qr Ò

1 ? ? ? ? ?

i

i ds

d

i qs

dt

i dr

i qr

I_e

1 ?

?

?

?

?

i

0

1 ?

?

?

?

?

?i

a10

V

ds

V_qs

a₅

0

0

(V.10)

+

0

a15

0

-

0

a20

0

0 0

- a a w - 2 .

1

Oil :

a 1 = a₇ = 4 . m1 . Lrc .Rs

a ₂ = a₆ = 4 . m1 . Lrc . Lrc

a ₃ = a₉ = 2 . m₁ . M_sr .N_r

a 4 = (L_rc .ù - S₂) .2 . m₁ . M _sr N r

.

a 5 = a₁₀ = 4 . m₁ . L rc

a 8 = (L_rc .ù + S₃) .2 . m₁ . M _sr . N_r

a11 = a17 = 6 . m1 . Msr . Rs

a 12 = a16 = ⁶ . m₁ . M sr . L sc

a 13 = a

? ( M N ) ? 1 ? = 1 . 3 . ^2 . + ? 19 sr r ? L rc ?

1

( ( ù 3 ) ) ?

? ?

a S M N S

2

= 3 . .

m L

- + . . - . ?

14 1 rc . sr 2

r ? L rc ?

a 15 = a₂₀ = 6 . m₁ . M sr

?

( ( ù 2 ) ) ?

1 ?

S M N S

2

a m L

= 3 . . . + . . - . ?

18 1 rc sr r 2 ?

L

rc ?

1

m₁ = ( -3. M _sr2 . N _r + 4. Lrc.L sc)

Et :

S 1 = 12 6 [( _r NR b 0 + R _b15 )cos² Oa +l ( N ux, b14 )cos² 15á

2 ^e +R 2 R e r + R_bl #177; R_b0 )cos² 1a + .^-P (2 R e r #177; R,, + R Ò 1

J

₁4 _rf

- RR _b° cos0 á cos1á) + (R_b1 cos 1 á cos 2á) +
·
·
· + (Rb15 cos15á cos0á)] (V.11)

6

i
? _I

S 2 = - 2 6 r r

[(2 R e + A₀ + g₁₅ )cos0 á sin0 á -(2 R e +R + A,₀ jcos1 á sin1 á (2 R e + g₁₅ +R_b14)cos1 5ásin1

N N_r

2 _rf

+ ₆ RR b 0 sin 0 á cos 1á ) + (R_b1 sin 1 á cos 2á ) +
·
·
· + (R_b15sin15á cos 0á )]

ri

+ ₆ RR _b° cos 0 á sin 1á) + (R_b1 cos 1 á sin 2á ) +
·
·
· + (Rb15 cos 15á sin 0á)] (V.12)

1

Oil : S1,S2, représente les résistances équivalentes des barres rotoriques

Le modèle mathématique discret peut être dérivé de l'équation d'état (V.10). Nous avons

Dans ces équations, A et B sont les matrices du modèle continu et AD, BD sont les matrices correspondants du modèle discret. k représente les instants discrétisés du temps et T_e est la période d'échantillonnage.

Alors, le modèle discret de la machine est décrit par l'équation :

x (k 1) [ 1 . ] . ( ) . . ( )

+ = + e

A T x k T B u k

+ e (V.13)

On considère que la vitesse est constante pendant les instants d'échantillonnage.

V.2.1 Modèle Discret Augmenté

La matrice A varie avec le temps aux éléments qui dépendent de la vitesse rotorique.

Lorsqu'un paramètre, dans ce cas les résistances équivalentes S1, S2 , sont inconnues, une autre équation doit être ajoutée au modèle de la machine; l'équation d'état n'est alors plus linéaire.

Pour estimer les résistances équivalentes, nous introduisons les équations :

S1 (k + 1 ) = S1(k)

S2(k+1) = S2(k)

Cette équation est basée sur I'hypothèse que les résistances équivalentes ne varies pas pendant l'intervalle d'estimation.

Le modèle complet de la machine est, donc :

[

I

1 1

x(k) BD(k)

0 0

.[ V_s ( k)]

S ₁ ( k + 1) = [ 0 1 0.[S ₁ (k ) J

+

(V.14)

x( k + 0

S ₂ ( k +1) j

0 0 _{1_1} S₂ (k) i 0

1)AD(k)

Le nouveau vecteur d'état, xn, est :

(V.15)

a₅ 0 i

0 a10

i sd ( k

i _qs (k

idr ( k

i _qr (k

I_e(k

S ₁(k

S ₂(k

1
i

+

1)

+

1)

+

1)

+

1)

+

1)

+

1)

+

1)

x(k) 1

x _n ( k) = S₁ (k ) =[ i _ds (k ) i _qs (k ) i _dr (k ) i _qr (k ) Ie(k ) S ₁ (k ) S₂ (O]^T S₂(k) j

Le modèle discret augmenté est

1 ? ? ? ? ? ? ? ?

?i

a₃ . S ₁ . Te a₄ .Te 0 0 0

a₈ .Te a₉ . S 1 .Te 0 0 0

a14 .Te 0 0 0

a17 .Te - a₁₈ . Te 1- a₁₉ . S ₁ 0 0 0

1 -Te.a 1 a.

2 w . Te -

-

a₇ .Te
. w. Te

a₆ .Te. w 1-

-

a11. ^Te a12

1 - a S Te

. . -

13 1

a16. w.Te

0 0 0

0 0 0

0 0 0

0 Le.Te 0 0

0 0 1 0

0 0 0 1

a

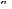
0

15

? ?? V ds

+ 0 - a .

? 20 Ò ? Ò

? V qs

? ?

0 0

?? ?

?

0 0

?? ?

0 0

J

?

L'équation de sortie est :

z ( k) = [i .ds (k) 1 qs (k)

1 _1

(V.16) (V.17)