5.3 Elément comprimé
Les éléments comprimés occupent une place
importante dans le domaine de la construction car ils transmettent l'ensemble
des charges gravitaires jusqu'aux fondations. Les efforts transmis sont
généralement dans l'axe de la colonne sauf dans les treillis.
Dans certains cas, il se peut que l'effort de compression soit couplé
avec un moment de flexion significatif, l'élément de structure
est considéré comme comprimé fléchi.
Dans la classification MCC, les colonnes se rangent
dans la classe 2, 3 ou 4 en fonction de l'accessibilité. Le remplacement
de ce type d'élément est donc permis cependant, même
fissurés ces éléments doivent pouvoir reprendre un
certaine quantité de charge.
L'ensemble des éléments comprimés peut
être victime d'une instabilité. Ce phénomène est
appelé flambement. L'élément a alors tendance à
fléchir dans la direction perpendiculaire à la charge.
5.3.1 Design
Il est intéressant de réfléchir aux
différents types de sections possibles pour les structures en verre
sollicitées en compression. Contrairement à l'acier où ils
existent des moules de différentes formes ou au béton où
l'on peut réaliser presque n'importe quelle forme de coffrage, les
structures en verre doivent être issues d'une composition de feuilles de
verre. De ce fait, plusieurs contraintes existent et limitent l'utilisation de
certains types de profile. Après réflexion, deux types de profile
sortent du lot dans le cas de structure soumise à une compression, celle
de forme circulaire et celle en forme de croix.
L'ensemble des profils creux n'est pas propice à
l'utilisation du verre car ceux-ci doivent être construit sous vide et
fermer de manière hermétique afin de prévenir toutes
infiltrations qui pourraient salir l'intérieur de la structure. Une fois
le tube fermé, il n'est plus possible d'y accéder afin de
l'entretenir. Cependant, des expériences ont déjà
été réalisées sur des profils circulaires creux.
De part la nature de la sollicitation et les risques de
flambement, il est plus intéressant d'avoir une structure doublement
symétrique afin d'optimiser l'utilisation de matière. De cette
manière on possède la même raideur (inertie) dans les deux
sens. Ceci est particulièrement intéressant s'il le type d'appui
est le même dans tous les orientations.
Enfin, l'assemblage de deux feuilles de verre perpendiculaires
se fait à l'aide de colles qui sont des points faibles de ce type des
profilés. Il semble donc utile et préférable de limiter
leurs utilisations au minimum.
5.3.1.1 La section circulaire
Même si les sections circulaires sont des profils creux
et que leur utilisation ne me semble pas être la plus appropriée
dans le cas de matériau transparent. Ils existent certains exemples de
réalisation et des recherches ont été effectuées
sur ce type de section. Il est vrai que la section circulaire est la plus
efficace dans le cas d'un effort de compression car elle dispose d'une plus
grande inertie pour une même quantité de matière. L'inertie
intervenant dans la résistance au flambement est donc importante. Dans
le tube, la matière est concentrée là où la section
en a le plus besoin, c'est-à-dire loin du centre de gravité.
Il est possible d'augmenter l'épaisseur de la section
circulaire. Il suffit de prendre deux tubes de verre de diamètres
différents et de compléter le vide entre les deux par de la
résine. La résine se solidifie grâce aux ultraviolets. On
obtient ainsi une colonne en verre feuilleté. Ces intercalaires
possèdent une faible rigidité et des faibles
caractéristiques de sécurité et d'habitude, ils ne sont
pas utilisés à des fins structurelles. Cependant, dans ce cas-ci
et à cause de la manière de procédé, il est
impossible d'utiliser une feuille plastique afin d'obtenir un verre
feuilleté.
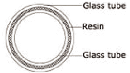
Figure 5.3 1 Section d'une colonne feuilletée [56]
5.3.1.2. La section cruciforme
Cette section est obtenue en prenant une feuille ou plusieurs
feuille de verre qui possèdent la longueur voulue. Après cela on
vient coller au milieu de ce premier élément, une ou des autres
feuilles de verre à 90° et cela de chaque coté afin
d'obtenir une croix.
Cette forme de section permet de limiter à deux le
nombre de joint de colle nécessaire. De plus, sa double symétrie
permet de s'affranchir d'une vérification supplémentaire et les
questions d'entretiens qui se posent dans le cas de structures creuses ne se
posent pas.
L'inertie d'une telle forme est intéressante même
si elle n'est pas optimale comme dans le cas d'un cylindre. Une partie de la
matière de la section se retrouve vite éloignée du centre
de la section.
L'inconvénient de ce type de section est la
présence de joint de colle supplémentaire qui sont obligatoire la
réalisation de cette section. L'utilisation de ce liant crée un
matériau non homogène. La rupture et l'instabilité de ce
genre de section n'a pas encore été étudiée en
profondeur ni les risques de flambements locaux (le risque qu'une des parties
collées ne flambe d'abord au lieu que l'ensemble de la section ne
subisse l'instabilité).
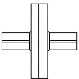
Figure 5.3. 2 Section transversale en croix
5.3.2 Etat limite ultime
D'après l'extrait repris au point 5.1.1, le calcul aux
états-limites ultimes d'une section en verre soumise à une
compression doit comprendre deux vérifications. La première est
la résistance de la section transversale et la deuxième est la
résistance au flambement.
5.3.2.1 Résistance des sections
transversales
Dans le cas d'une section soumise à une compression pure,
sans tenir compte des instabilités, la formule pour déterminer la
charge maximale que peut reprendre une feuille de verre est la suivante :
Nc , rd = fg , c , d
. A (5.4)
Nc , rd = Valeur de l'effort normal
fg , c , d = Résistance de
calcul en compression A = Aire de la section
Dans le cas du verre laminé composé de n feuilles
de verre, la formule devient :
Nc , rd = fg , c , d
. Aeff (5.5)
Nc , rd ; fg , c , d
ont déjà été expliqués
Aeff = Aire effective, aire qui participe à la
résistance
Le verre feuilleté est un mélange entre des
feuilles de verre et un film plastic adhésif. Ce film comme tous les
éléments possède une épaisseur, il est
préférable de négliger cette quantité de
matière car cette approximation nous met du côté de la
sécurité. L'aire totale d'un verre feuilleté est donc
l'aire de chacune des feuilles de verre.
A = ? A (5.6)
eff i
i
Ai = Aire de la feuille de verre i
5.3.2.2 Résistance au flambement et
résistance à la traction transversale
Le flambement est un phénomène
d'instabilité qui existe lorsqu'un élément est soumis
à un
effort de compression. Sous un effort axial,
l'élément se met à fléchir dans la direction
perpendiculaire à celle de la charge, ceci explique sa
dénomination complète «flambement par flexion ». Ce
phénomène apparaît avant la ruine du matériau, il
est donc important de déterminer la charge critique maximale par rapport
à ce phénomène.
La détermination de la résistance au flambement
d'une structure soumise à un effort de compression fait partie de la
vérification aux états-limites ultimes d'une structure. Dans le
cas du verre, les formules du flambement eulérien ne comprennent pas
seulement un terme en compression mais également un moment dû
à l'excentricité des efforts. Les parties sollicitées en
traction sont les parties dimensionnantes de la structure. En pratique, la
réalisation d'assemblage permettant une transmission des efforts par
compression pure est totalement illusoire. Cependant, cette formule est bien
celle que l'on utilise en général pour avoir une idée de
la valeur maximale de la charge critique. On se permet de négliger les
efforts du second ordre car les autres matériaux peuvent plastifier et
ainsi limiter voir empêcher la propagation des fissures. Dans le cas du
verre, le phénomène de propagation sous-critique (voir chapitre
3) amène à la ruine même sous chargement constant car c'est
un matériau fragile. De plus, on sait également qu'il existe
certaines tolérances vis-à-vis de la construction d'une feuille
de verre. Les feuilles de verre trempé possèdent toujours une
légère flèche qui contribue à augmenter l'effet de
second ordre existant.
Dans le cas du verre, la formulation de la charge critique
d'Euler donne une valeur maximale de la charge admissible. La loi d'Euler se
base sur deux hypothèses :
- utilisation d'un matériau parfaitement
élastique
- On admet qu'il n'y a aucune tension ne dépassant la
limite proportionnelle
Pour une feuille de verre simple, la première
hypothèse est vérifiée mais la deuxième n'est
jamais vérifiée, peu importe le matériau. La formule
d'Euler est valable pour un matériau possédant une
résistance infini. L'instabilité interviendrait de manière
instantanée. La réalité est différente, lors d'un
essai en compression, la charge augmente petit à petit et l'on peut voir
une flexion apparaître dans l'élément. Quand la charge
critique est presque atteinte, il y a une bifurcation soudaine de
l'élément.
Dans le cas d'une feuille de verre simple et grâce
à son caractère élastique, la charge critique d'Euler
donne une valeur satisfaisante pour la charge critique de flambement sans pour
autant prendre des coefficients de réduction.
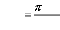
2
EI
N
cr , e 2
L k
(5.7)
E = Module de Young
I = Inertie de la section
Lk = Longueur caractéristique
La formule a été établie pour des
éléments comprimés bi articulés. Cependant, il est
possible de fixer les colonnes de plusieurs manières différentes.
Il est donc important de connaître les longueurs de flambement dans ces
autres cas. Il existe des abaques avec différents types d'appuis et la
longueur de flambement relative, la figure 5.3.3 reprend la valeur de la
longueur de flambement de différents cas simples.
La détermination de la charge critique d'Euler n'est
pas suffisante dans le cas d'une structure en verre. Un élément
n'est jamais en compression parfaite, il y a toujours des excentricités
des charges. Ces excentricités induisent des efforts de second ordre et
des zones en traction peuvent apparaître qui sont
déterminantes.
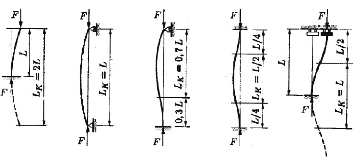
Figure 5.3. 3 : Valeurs de la longueur caractéristique de
flambement dans différents cas [35]
Le dimensionnement des structures en verre soumises à un
effort de compression peut se faire selon deux principes :
- par un calcul au deuxième ordre (résistance
à la traction transversale) - par la détermination de la
résistance au flambement
Voici donc les formules préconisées pour la
vérification de la contrainte [49] pour le calcul au état limite
ultime en compression.
Dans le cas d'une feuille de verre simple Dimensionnement
par un calcul au deuxième ordre :
N N ? e w ?
ó = #177;
0
? + ? = f (5.8)
g t d
, ,
A W ? cos / 2 /
L N EI 1 / ,
- N N
? k cr e ? ?
A = Aire de la section
W = Module de section élastique e =
excentricité
w0 = flèche initiale
Ncr , e = charge critique d'Euler
La valeur de la flèche initiale w0 est
donnée dans le chapitre 3, l'usage conseillerait de
prendre la valeur de tolérance de construction la plus
grande de la flèche globale dans le cas du verre trempé
thermiquement et horizontalement.
L'excentricité dépend de plusieurs
paramètres tels que le type d'assemblage, le type d'appui ou bien encore
la position de l'élément au sein de la structure. On ne peut pas
généraliser la valeur e. C'est l'ingénieur qui doit
déterminer cette valeur en fonction de la condition de fixation des
extrémités de la colonne. Comme il n'y a pas des détails
types elle peut être différente pour chaque application.
Dimensionnement par l'utilisation d'un coefficient de
réduction :
D'après la référence [49], le coefficient
de réduction ne peut pas être déterminé à
partir des courbes de flambement. L'auteur propose une autre méthode
pour la détermination de la résistance de calcul au flambement en
se basant sur l'utilisation d'un coefficient de réduction.
Nrd , b = ÷b . A
. fg , t ,d (5.9)
Nrd , f = La résistance de calcul au
flambement ÷b = Coefficient de réduction
A = Aire de la section
fg ; t , d = Résistance de
calcul de traction d'une feuille de verre
La valeur du coefficient de réduction est obtenue à
partir du graphe (voir Figure 5.3.4) et de l'élancement réduit
ë
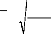
fg , t , d
ók
ë
(5.10)
ók = Contrainte dans la section pour
une charge en compression d'Euler
Dans la formule du flambement, il peut paraître
étonnant de voir apparaître la résistance
caractéristique en traction du verre. Comme la résistance en
compression est très élevée pour le verre, la
capacité portante d'une colonne en verre en compression est toujours
limité par la résistance en traction due à la flexion de
l'effet du second ordre.
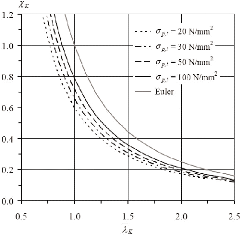
Figure 5.3 2 Courbes pour la détermination du coefficient
de réduction en fonction du flambement [49]
( ó p , t = fg ; t ,
d )
Contrainte maximale en compression pour une feuille de
verre
La valeur de contrainte maximale que peut supporter un
élément en verre soumis à une charge de compression est la
plus petite des valeurs obtenues par les différents
procédés de dimensionnement de la charge critique de flambage.
Tous les termes de cette formule ont déjà été
expliqués précédemment.
|
ómax,b
|
? ? N N ? e w ? N
?
0 rd b ?
,
= min ? #177; ? + ? ; ? (5.11)
cos / 2 / 1 /
? ? A W ? L N EI - N N A
? k cr e
, ? ? ? ?
|
Dans le cas d'un verre feuilleté composé de
n feuilles
A cause de la présence de feuilles plastiques dans le
verre feuilleté, le comportement mécanique est
légèrement différent de celui d'une feuille en verre
simple. Le caractère plastique du film adhésif donne au
matériau un caractère plastique. Il faut utiliser la
théorie élastique des éléments « sandwich
» afin de représenter le plus correctement le comportement des
verres feuilletés.
ð á ð áâ
2(1 + + 2 ) EI s
N = (5.12)
cr K
, 1 2
+ ð â Lk2

2
=
i
2
i n
=
Lk
G b
PVB
( )2
? z i
i n
=
? (5.13) ;
I
i 2 i
=
I s
t EI
PVB s
i n
=
I b t z
s = ? i i
á =
â =
(5.14) ;
2(5.15)
i = 2
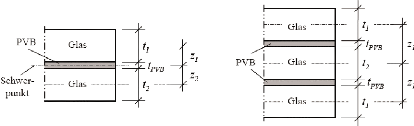
Figure 5.3 3 Verre feuilleté avec 2 intercalaires et 3
intercalaires [49]
b = longueur
z = distance entre le milieu de l'intercalaire et le
milieu de la feuille de verre
Une autre approche a été
développée qui tend à généraliser le
comportement mécanique des éléments soumis à une
charge de compression. Dans le cas de verre feuilleté, la section
sandwich pourrait être remplacé par une section monolithique avec
une épaisseur effective donnée par la formule suivante [49].
« Pour des charges de longue durée comme le poids propre ou
pour des températures supérieures à 30°C, la
contribution du PVB peut être
négligée. Le comportement
visco-élastique peut être simplifié par l'utilisation d'un
module de glissement élastique équivalent, ce qui permet un
calcul élastique du système. »[23J :

( 1 + +
á ð áâ
2 )
b ( )
1 2
+ ð â
12 I s
3
=
teff
(5.16)
teff = largeur efficace
á , â , Is
,b ont été expliqués au point
précédent
L'utilisation de cette valeur efficace permet de se rapporter
aux formules relatives à une
seule feuille de verre simple. Il faut
juste remplacer la valeur de b par la valeur de teff et
de
changer tous les termes où la largeur intervient.
5.3.2.3 Résistance à la torsion flexion de
la section cruciforme
De part la géométrie et le mode de fabrication
des éléments vitrés, il semble important et indispensable
d'appliquer la théorie relative aux parois minces à ces
éléments. Il faut donc ajouter cette vérification pour
s'assurer du bon dimensionnement de la structure. Les formules proposées
ici seront celles relatives à la section cruciforme (voir 5.3.1). C'est
la section qui convient le mieux pour ce type de matériau et ce type de
sollicitation. La formule de la capacité portante maximale d'une section
possédant une double symétrie et soumise au flambement en
torsion-flexion est la suivante [33] :
|
N=
cr K
,
|
1 ( ð 2 )
EI w
GK +
i L
0 2 k 2
|
(5.17)
|
i0 = le rayon de giration de la section par
rapport au centre de torsion
K = Inertie de torsion
Iw = Inertie sectorielle principale G
= Module de glissement
Dans le cas d'une section cruciforme, le terme
Iw = 0, ceci permet donc de supprimer toute
la deuxième partie de la formule.
L'inertie de torsion d'une section ouverte est donnée par
la formule suivante :
1
K = ? L e (5.18) 3 i i 3
i
Li = longueur des différents
éléments
ei = épaisseur des
différents éléments
Le module de glissement est une donnée relative de
chaque matériau présent. Dans le cas du verre feuilleté,
le comportement visco-élastique peut être simplifié par
l'utilisation d'un module de glissement élastique équivalent, ce
qui permet un calcul élastique du système.
La rigidité de torsion de Saint-Venant peut donc
être calculée de la manière suivante :
GK = ? GK (5.19)
eff i
i
Dans cette formule, i représente l'ensemble des couches
présentes indépendamment de la nature de leur matériau
(verre et film plastique).
5.3.3 Etat limite de service
Dans le cas de structure en verre soumise à
compression, la seule vérification à faire est une
vérification de la déformée. Ils n'existent pas d'autres
risques ou contraintes concernant l'aspect ou la sécurité des
personnes. Le risque de fissuration ne doit pas être pris en compte dans
le calcul à l'état limite de service car dès qu'une
fissure apparaît, celà mène directement à la
ruine.
5.3.3.1 Deformation
Comme pour l'état-limite ultime, les effets du second
ordre ont un effet important sur la déformé, il faut donc les
prendre en considération.
Concernant la valeur admissible de la flèche, selon la
norme belge NBN B 03-003 [50], la flèche la plus contrainte est celle
relatif au confort visuel. C'est la valeur de la flèche en sommet de
colonne.
h
f = (5.20)
250
h = Hauteur de l'élément
Dans la norme belge, il n'y a pas de dispositions concernant la
flèche maximale au milieu de la colonne. Il faudrait donc prendre les
mêmes dispositions que pour une poutre :
h
f = (5.21)
300
La formule pour déterminer la flèche au milieu de
la colonne si on ne considère qu'une force axiale et tenant compte
également des effets du second ordre est :
e
w = +
cos( k / 2 / cr ) 1 / cr
L N N - N N
w0
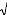
(5.22)
Cette formule est la même que ce soit une feuille de verre
simple ou bien un verre feuilleté. La différence entre les deux
se fait au niveau de la détermination de la charge critique
Ncr .
| 


