Conception et calcul des structures en verre

5.2 Classifications des structures 5.2.1 Généralité

Des chercheurs néerlandais de l'université de Delf (TU Delf), on mit au point une nouvelle approche de classification de structure pour le verre. Dans les normes européennes actuelles, on limite le risque avec une approche probabiliste. Pour ces chercheurs, la question à se poser ne devrait pas juste être « Quand le verre se cassera » (approche probabiliste) mais « Que se passera-t-il quand il sera casser » (approche basé-

conséquence) (Phrase traduite de l'anglais : `when will the glass break ?' ( probalistic approach) but also `what will happen when is does' (consequence-based approach)[13] . En réalité, les concepteurs se soucient déjà de ce problème en utilisant certaines méthodes comme par exemple le verre feuilleté. Cependant, ces différentes méthodes ne sont pas réglementées et elles dépendent de l'expérience et de l'opinion de l'ingénieur, la localisation, le type de structure et encore d'autres paramètres.

Dans les normes actuelles, la notion de risque a été introduite qui est un produit entre la probabilité qu'un élément se fissure et la conséquence de cette fissure. Pour une approche probabiliste complète, il est important de connaître toutes les données relatives aux propriétés structurales du matériau et des actions sur la structure. En réalité, on utilise des approximations et des estimations basées sur l'expérience et les recherches. Dans le cas du verre, le manque de connaissance et de formulations claires concernant le comportement après fissuration rend difficile l'approche traditionnelle.

Les chercheurs de l'université de Delf ont donc décidé de mettre au point une méthode. Ils ont introduit un nouveau concept MCC (Member Consequence Classes). C'est un classement des éléments fissurés qui se base sur les contraintes résiduelles de ces éléments pour une certaine période en fonction d'un niveau de dommage. Cette nouvelle approche permet de créer un outil de comparaison entre les différentes structures. Ce nouveau classement des éléments de structure se base sur le rôle et la fonction des différents éléments au sein de la structure et l'accessibilité de la structure.

5.2.2 Les paramètres

Deux paramètres ont déjà été cités plus haut, il s'agit de la résistance des contraintes résiduelles et le temps durant lequel la structure va résister après que la fissure soit entamée.

La fissure d'un élément en verre peut avoir plusieurs formes. Un verre feuilleté est considéré comme fissuré quand l'ensemble de ces feuilles sont fissurées mais aussi quand seulement une de ces feuilles l'est (voir Figure 5.2.1).

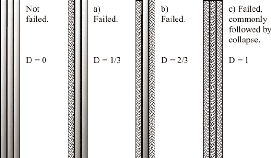
Figure 5.2 1 Schéma représentatif du niveau de dommage d'un élément en verre [13]

Il est normal de considérer plusieurs cas différents de post-fissures en fonction des
différents types de dommages. Afin de faire la distinction, le concept de dommage _Dglass a

été introduit comme étant le troisième paramètre de cette approche de sécurité. 5.2.3 Axes de démarcations

5.2.3.1 Le dommage

Quand une feuille se rompt, la fissure se propage le long de toute la feuille. Cette
caractéristique permet de considérer le dommage comme une fonction du nombre de
feuilles de verre. Le paramètre Afr, c (la surface fissurée) peut être affinée en ne considérant

que la partie réellement fissurée et non pas comme si toute la feuille de verre l'était (voir Figure 5.2.2)

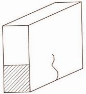
Dglass

A fr , c

Figure 5.2 2 Représente l'aire frontale en hachuré

Atot

= (5.3)

A fr ,c = Aire frontale fissurée Atot = Aire totale

5.2.3.2 La contrainte

La contrainte au sein d'un élément est différente en fonction des combinaisons d'actions et des usages. Le niveau de contrainte exigé pour un élément peut être le même que celui-ci soit endommagée ou bien qu'il ne le soit pas.

Ssw = Contrainte égale au poids propre de l'élément S_mom = Contrainte égale à un chargement momentané Ssls = Contrainte égale à l'état limite de service

Suls = Contrainte égale à l'état limite ultime Srep = Contrainte égale à la rupture du verre 5.2.3.3 Le temps

Peu d'informations existent pour déterminer le temps pendant lequel la contrainte recommandée peut être maintenue. Voici les temps de référence proposés :

30 sec : Temps nécessaire pour fuir immédiatement d'un dommage d'un élément structurel

2h : Temps nécessaire pour évacuer et fermer un espace autour d'un membre endommagé 24h : Temps pour prendre des mesures structurelles (étançonnement)

72h : Temps pour prendre des mesures structurelles complémentaires

tref : Temps de référence pour la vie du bâtiment

5.2.3.4 Member Consequence Classes (MCC)

Il est maintenant possible de déterminer un tableau en fonction du rôle de la structure dans le bâtiment et son accessibilité. Contrairement à l'eurocode qui classe les structures en fonctions seulement de leur importance, de leur rôle dans le bâtiment. 6 classes différentes ont été proposées.

Rôle au sein de la structure Accessibilité de la structure MCC

Structure clé Élevé - Espace Publique 6

Structure clé Moyen - Espace semi publique/ bureau 6

Structure clé Bas - privé 5

Structure principale Élevé - Espace Publique 4

Structure principale Moyen - Espace semi publique/ bureau 3

Structure principale Bas - privé 2

Structure secondaire Élevé - Espace Publique 3

Structure secondaire Moyen - Espace semi publique/ bureau 2

Structure secondaire Bas - privé 1
Tableau 5.2 1 : Tableau de classification des structures [13]

MCC	d<1 (pré fissuré) contrainte temps		d=1 (extérieur) Contrainte temps		d=m (toutes les feuilles extérieures) contrainte temps		d= n (toutes les feuilles) contrainte temps
1 2 3 4 5 6	Suls Suls Suls Suls Suls Suls	tref tref tref tref tref tref	Suls Ssls Suls Ssls Suls Suls Suls Srep	2h 24h 24h 72h 72h tref tref tref	Smom Suls Ssls Suls Ssls Suls Ssls Suls Srep	30sec 2h 24h 24h 72h 72h tref tref tref	0 Smom Smom Ssls Smom Suls Ssls Srep	0 30sec 2h 24h 72h 24h 72h tref

Tableau 5.2 2 Temps et contraintes recommandées pour une certaine valeur de dommage [13]

Cette classification est pour l'instant difficile à établir car la résistance de calcul d'une feuille de verre endommagée n'a jamais été véritablement étudiée.