Chapitre IV
Application
4.1- Introduction.
Nous avons jusqu'à présent
développé le modèle nécessaire du système de
puissance, présenté la théorie de la stabilité aux
petites perturbations avec régulateurs PSSs ainsi que les AGs.
L'objectif de ce chapitre est de trouver la meilleure localisation possible des
PSSs, avec des paramètres optimaux, tout en réduisant le nombre
de PSSs. Cela assurera un amortissement satisfaisant aux oscillations
rotoriques des modes locaux et interrégionaux et garantira la
stabilité globale du système pour différents points de
fonctionnement.
Lors de l'installation des PSSs dans les réseaux
multimachines, la première étape conventionnelle à mettre
en oeuvre concerne la détermination des meilleurs emplacements des PSSs
au sein du réseau.
Le nombre de stabilisateurs à installer n'est pas
toujours égal au nombre de générateurs. Par
conséquent, il faut prendre en considération le choix de
l'emplacement optimal des stabilisateurs qui offre un meilleur
amortissement.
Pour amortir les modes locaux, le choix de l'emplacement reste
facile car le nombre de générateurs impliqués
principalement dans les oscillations locales est très faible. Par
contre, pour les modes globaux, un grand nombre de générateurs
sont généralement associées aux oscillations. Cela
complique le choix de l'emplacement des PSSs (Zhou et al., 1991). En
outre, une mauvaise localisation d'un PSS peut entraîner une
amplification des oscillations, voire contribuer à la perte de
stabilité du système. Ainsi, le problème du choix de
l'emplacement des PSSs est très critique et il faut le traiter
judicieusement.
Quand un PSS est inséré dans le système,
il affectera tous les modes électromécaniques d'oscillations.
Ainsi, les interactions entre les PSSs doivent être
considérées lorsque plusieurs PSSs sont insérés
(Zhang et al., 2000).
Tout PSS devrait être réglé pour fournir
l'amortissement suffisant de tous les modes électromécaniques car
l'amortissement de chaque mode est un effet cumulatif des contributions de
chaque PSS. En outre, le réglage des PSSs doit être robuste : les
PSSs doivent être efficaces non seulement lors de la variation des
conditions de fonctionnement mais aussi lors du changement de la topologie du
réseau.
Ce chapitre s'articule autour de l'application de notre approche
au sein d'un système de puissance multimachines.
Dans la première partie, nous allons présenter les
caractéristiques du réseau étudié (le réseau
interconnecté New England/New York : 16 générateurs et 68
noeuds).
Ensuite, nous expliquons les différents critères de
performance du système pour le modèle linéaire et
non-linéaire.
Le problème d'assurer une meilleure localisation des
PSSs et une meilleure coordination de leurs paramètres est
formulé en tant que problème d'optimisation multiobjectif et
résolu à l'aide d'un programme d'AG. La fonction multiobjectif
utilisée est formulée pour optimiser un ensemble de deux
fonctions objectif basées sur l'analyse des valeurs propres du
système (partie réelle de la valeur propre et facteur
d'amortissement). La mise en oeuvre de cette approche fera l'objet de la
troisième partie du chapitre.
La dernière partie du chapitre concerne l'application de
l'approche proposée et la discussion des résultats obtenus.
4.2- Réseau étudié.
4.2.1- Caractéristiques du réseau
étudié.
Le système de puissance choisi dans notre étude
est le réseau réduit équivalent au réseau
interconnecté de New England et New York (Rogers, 2000). Ce
système, composé de cinq régions, possède des
propriétés intéressantes de par la complexité des
interactions des différentes régions qui le composent. Il se
compose de 16 générateurs (numérotés de 53 à
68) et de 68 noeuds. Les neuf premiers générateurs
représentent le système de génération de New
England. Les générateurs de 62 à 65 représentent le
système de New York. Chacun des trois derniers générateurs
forme un seul groupe ; ils représentent les systèmes
équivalents aux trois grandes régions voisines
interconnectées au système de New York.
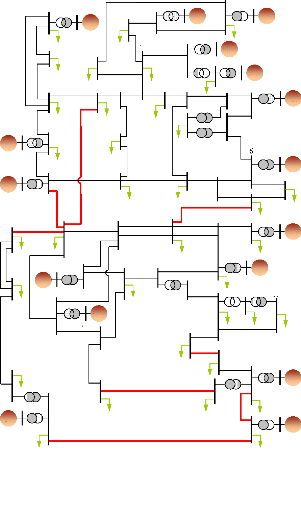
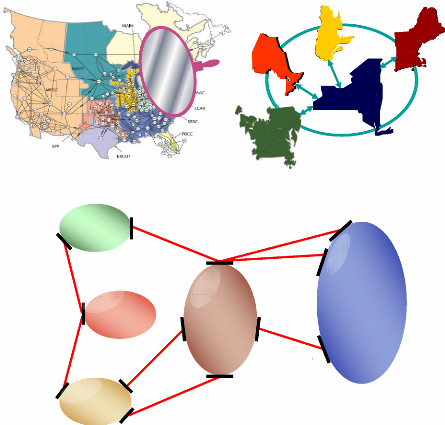
La représentation unifilaire du système et une
représentation géographique et schématique de
l'interconnexion des cinq régions sont respectivement données aux
figures (46) et (47). Huit lignes d'interconnexion relient les cinq
régions du système : ce sont les lignes entre les jeux de barre
(1#2), (1#27), (1#47), (8#9), (42#41), (46#49), (52#42) et (50#51). La
puissance est transférée de la deuxième région aux
première, troisième et cinquième régions. La
puissance est aussi transférée de la cinquième
région à la quatrième et de cette dernière à
la troisième. Les puissances active et réactive transitées
dans ce réseau, pour le point de fonctionnement nominal, sont d'environ
20 GW et 3 GVAr. Cela représente quasiment, en ordre de grandeur, un
quart que le système de puissance français.
Les valeurs numériques du réseau peuvent être
trouvées dans la référence (Rogers, 2000) ; elles sont
rappelées en annexe C.
4.2.2- Caractérisations d'un
défaut.
Dans les réseaux haute tension, les types de
défauts les plus fréquents sont les courts- circuits. Ces
derniers dépendent de différents facteurs tels leurs
emplacements, leurs durées, leurs types (une phase- terre, deux
phases,...), le système de prise de terre,... .
Bien que les courts-circuits triphasés -les
défauts symétriques- soient rares, l'analyse de ce type de
défauts est nécessaire, car ils mènent
généralement aux courants de défauts les plus
sévères. Ils sont donc souvent les plus utilisés en
simulation dynamique pour tester la stabilité des systèmes de
puissance et la robustesse de régulation.
Lorsque les protections détectent une apparition de
courants élevés sur une ligne (ou une diminution de
l'impédance vue des extrémités de la ligne), elles
"envoient" aux disjoncteurs concernés un ordre d'ouverture afin d'isoler
la ligne en question et éviter la propagation du phénomène
sur le réseau. La disparition du court-circuit doit se faire rapidement,
en moins de trois périodes du réseau (50 millisecondes pour une
fréquence de 60 Hz). Ensuit, les dispositifs de réenclenchement
automatique de la ligne sont responsables de remettre la ligne en service
(Meyer et al., 1998). Ainsi, la simulation du défaut de
court-circuit sur une ligne de transmission et la simulation du comportement
des systèmes de protection s'effectue lors de :
- l'apparition du défaut
- l'ouverture et du réenclenchement automatique des
disjoncteurs.
Dans notre étude, cela implique de calculer la matrice
admittance du réseau de transport pour les trois phases suivantes :
avant le défaut, pendant le défaut et après le
défaut, en considérant que le défaut triphasé est
caractérisé par une impédance infiniment petite
(Zf = 0 + j10-7 dans notre simulation), (Tolba,
2005).
29
59
61
23
58
22
21
G6
G7
52
40
68
G9
19
56
G4
28
24
16
57
20
G5
27 17
15 14 13 10
55
26
G3
60
25
18
12 11
G8
54
53 2
G1
3
4
7
5
G2
8
36 37 65
9
1
30
47
G13
63
32
64
G12
33 34
48
G11
45 44 39
31
35
G10
62
51
50
38
G16
46
41
66
67
49
42
G15
G14
Figure 46. Représentation
unifilaire du réseau étudié
(Réseau New
England/New York : 16 générateurs, 68 noeuds).
105
47
2
Région
3
41
1
27
42
49
9
New
York
8
Région
4
Région
2
New
England
Région
1
46
52
50
Région
5
51
ISO
IESO
New York
ISO
PJM
MW*
Hydro
Quebec New
England
Figure 47. Représentation
géographique et schématique des cinq régions du
système étudié. 4.3- Analyse de la
performance et critères de bonne régulation.
Pour faire une étude analytique complète des
problèmes d'oscillations des systèmes de puissance, il est
nécessaire d'établir des procédures d'analyse du
problème et de préciser les critères de performance du
système. Les outils d'analyse des oscillations du système doivent
déterminer les problèmes existants ; ils doivent être
capables en outre d'identifier les éléments déterminants
et de fournir des informations utiles pour la conception et le réglage
des contrôleurs du problème.
Les simulations d'un système non-linéaire en
domaine temporel, qui représentent une extrapolation naturelle de
l'analyse de la stabilité transitoire, fournissent des informations
importantes mais limitées en ce qui concerne la stabilité
dynamique. Ainsi :
- le choix de la perturbation et la sélection des
variables à observer sont critiques,
- la perturbation peut être insuffisante pour exciter les
modes critiques,
- les réponses temporelles ne peuvent donner directement
une information sur la source des oscillations,
- plusieurs modes sont mélangés dans les courbes
des simulations temporelles.
L'analyse du modèle linéaire du système
semble un moyen idéal pour étudier profondément les
oscillations électromécaniques et les problèmes
associés. La stabilité et les caractéristiques de chaque
mode peuvent par exemple être identifiées clairement en examinant
les valeurs propres du système. Les vecteurs propres quant à eux
montrent aisément la nature de ces modes et les relations entre eux et
les variables d'état.
Ainsi, une compréhension complète des
oscillations de système de puissance nécessite la combinaison
d'outils analytiques. L'analyse du modèle linéaire
complétée par des simulations en domaine temporel du
modèle non-linéaire représente la procédure la plus
efficace pour bien étudier et analyser les oscillations de
système de puissance (Farmer, 2006). Les étapes suivantes sont
nécessaires pour une étude systématique des oscillations,
figure (48) :
1- examen des valeurs propres du système. Il indique
la présence des modes mal ou non- amortis. L'analyse modale de ces modes
permet de déterminer leurs caractéristiques et leurs origines.
2- réalisation des simulations du système
non-linéaire dans le domaine temporel pour les cas critiques
identifiés par l'analyse modale. Cela confirme les résultats de
l'analyse du modèle linéaire et montre en plus l'influence de la
non-linéarité du système sur les oscillations.

Stabilité transitoire
Transition dynamique d'un point de
fonctionnement à
un autre.
Modèle non-linéaire
Simulation (Analyse
temporelle)
Méthodes d'intégration numérique.
Stabilité dynamique
Variation dynamique autour d'un point
de fonctionnement.
Modèle linéaire
Analyse du modèle
linéaire
Analyse des valeurs propres
et analyse
modale.
Figure 48. Analyse des oscillations d'un
système de puissance.
Enfin, en supposant que le réglage des
contrôleurs est fait au point de fonctionnement nominal du
système, il est nécessaire de vérifier la robustesse du
réglage. Dans le contexte du réglage du contrôleur
d'amortissement d'un système de puissance, la robustesse signifie que
l'amortissement est suffisant et que les oscillations s'amortissent rapidement
lors des simulations temporelles du système pour toutes les
perturbations probables et pour tous les points de fonctionnement
significatifs. Ainsi, les critères de bonne régulation doivent
être respectés pour tous les scénarios
considérés (Pal et al., 2005).
4.3.1- Critères d'analyse du modèle
linéaire.
Rappelons que le facteur d'amortissement Ç d'un
mode représenté par sa valeur propre complexe )L est
donné par :
ó
-
=
(130)
ó 2 ù
2
+

æ
Avec : ë= ó #177;
jù (131)
- Un facteur d'amortissement Ç important
aboutit à une réponse dynamique bien amortie. Pour cela, toutes
les valeurs propres doivent se trouver dans la zone gauche du plan complexe
limité par deux demi-droites issues de l'origine, figure (47). Pour une
valeur critique du facteur d'amortissement Çcr : on impose
alors une marge de stabilité relative (Allenbach, 2005, I).
- La partie réelle de la valeur propre
ci
· détermine la rapidité de
décroissance/croissance des exponentielles composant la réponse
dynamique du système. Ainsi, ci
· très
négatif aboutit à une réponse dynamique rapide. Pour cela,
toutes les valeurs propres doivent se trouver dans la zone gauche du plan
complexe limité par une verticale passant par une valeur critique de la
partie réelle (ci
·cr), figure (47) : on
définit ainsi la marge de stabilité absolue.
Lors du réglage des paramètres des PSSs, il est
souhaitable que ces deux critères soient pris en compte pour permettre
une bonne régulation. La combinaison entre ces deux critères
aboutit à une zone appelée zone de stabilité D,
(Yee et al., 2004), figure (49). Le déplacement des valeurs
propres dans cette zone garantit une performance robuste pour un grand nombre
de points de fonctionnement (Singh, 2004).
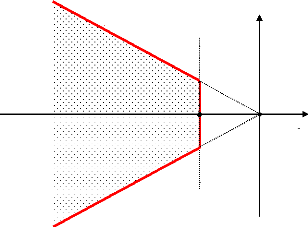
æcr
joi
ci
·
ócr
Figure 49. Zone de la stabilité
D.
Considérons par exemple un mode d'une fréquence
naturelle de 1 Hz, les oscillations associées à ce mode
s'amortissent en 13 secondes pour Ç = 0.05 et en 6.5 et 3
secondes pour Ç = 0.1 et Ç = 0.2
respectivement. Quelle est alors la valeur minimale adéquate
d'amortissement pour un bon fonctionnement du système de puissance?
La littérature ne présente pas de valeurs
critiques rigoureuses admises par tous. Généralement, un facteur
d'amortissement de 0.05 n'assure qu'une petite marge de sécurité
tandis que Ç = 0.03 doit être accepté avec
réserve. Les valeurs d'amortissement entre 0.05 et 0.15 sont globalement
les plus utilisées dans la littérature. Nous avons choisi
Çcr = 0.1 comme facteur d'amortissement critique. Ainsi, nous
considérons que l'amortissement des oscillations est suffisant si tous
les modes du système présentent des facteurs d'amortissement plus
grands que Çcr.
D'une façon similaire, la littérature donne une
gamme de variation de la valeur critique de la partie réelle des valeurs
propres, comprise entre - 0.5 et - 1. Nous avons choisi ocr = - 1
comme partie réelle critique à respecter par tous les modes.
Enfin, d'autres spécifications peuvent être
utilisées telles les spécifications de la réponse du
système dans le domaine temporel (le dépassement maximum, le
temps d'établissement, l'erreur statique, ...), (Yee et al.,
2004).
4.3.2- Critères de simulation.
La performance d'un contrôleur nécessite des
critères pour évaluer le "bon" comportement du système.
Elle peut être spécifiée dans le domaine temporel et/ou
fréquentiel (Pal et al., 2005).
Les caractéristiques dynamiques peuvent être
décrites en examinant la réponse à une entrée
typique (tel un échelon unité, ...). Ainsi, les
spécifications de la réponse transitoire (tels le
dépassement maximum, le temps de réponse, le temps de pic, ...)
tout comme les critères intégraux (tels IAE, ISE, ITAE, ...)
peuvent être utilisés comme indicateurs de performance des boucles
de régulation (Aström et al., 1995).
4.3.2.1- Critères temporels
instantanés.
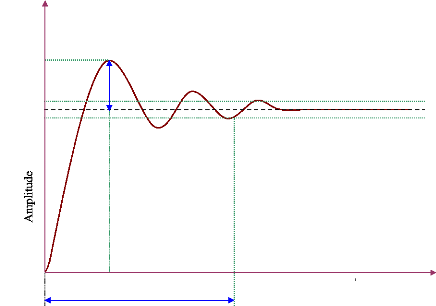
La réponse indicielle (réponse à un
échelon unité) d'un système oscillant du deuxième
ordre est donnée à la figure (50), (Allenbach, 2005, I).
Nous définissons les paramètres critiques
apparaissant sur cette figure : 1- Dépassement
maximum Dp
Il est la mesure de la valeur maximale atteinte par la
réponse indicielle lors de son premier dépassement. Cette valeur
est souvent pondérée par la valeur finale : on parle alors de
dépassement maximum en pour cent, noté Dp% et
calculé par la relation suivante.
% max · 100
y y
D (132)
- f
=
y
p
f
Le dépassement maximum s'exprime en fonction du facteur
d'amortissement comme suit :
ðæ

2
Dp =e (133)
1 - æ
ymax
Dp
105 % 100 % yf
95 %
tp
Temps
0
tr (5 %)
Figure 50. Caractéristiques de la
réponse indicielle d'un système. 2-Temps de
pic tp
Ce paramètre correspond à l'abscisse du
dépassement maximum. Ce paramètre de temps peut être
déterminé analytiquement en fonction du facteur d'amortissement
et de la pulsation naturelle d'oscillation, comme suit :
ð
tp (134)

2
=
ù n
1 æ
-
3- Temps de réponse (temps
d'établissement) tr(5%)
Il correspond au temps nécessaire à la
réponse indicielle pour atteindre sa valeur finale avec une
tolérance de #177;n% près. La tolérance de 5% est
la plus communément utilisée. Ce paramètre
caractérise la rapidité relative de la réponse du
système. La relation approximative entre le temps de réponse, le
facteur d'amortissement et la pulsation naturelle d'oscillation est
donnée comme suit :
3
t ù æ avec
< æ <
, 0 1 (135)
r (5 %)
n
La valeur critique du temps de réponse de la
stabilité dynamique (dite aussi stabilité dynamique) varie d'un
opérateur de système de puissance à l'autre.
Généralement, elle s'étend de 10 à 20 secondes (Pal
et al., 2005).
Finalement, nous pouvons remarquer qu'une augmentation du facteur
d'amortissement aboutit à une diminution du dépassement maximum
et du temps de réponse.
4.3.2.2- Critères temporels
intégraux.
Soit å(t) l'erreur dynamique
associée à la réponse indicielle du système.
Différents critères typiques peuvent être utilisés
pour caractériser la performance du système régulé.
Nous les définissons ci-dessous.
1- Critère IAE, Intégrale de
l'Erreur Absolue (Integral of Absolute Error). Le critère
de performance est le suivant :
t
e( ) (136)
t dt
IAE j.

0
Etant donné que ce critère prend en compte tous
les éléments de la réponse harmonique, il donc important
lorsque la réponse du système est oscillatoire ; les faibles
amortissements ne sont pas ainsi conseillés.
2- Critère ISE,
Intégrale du Carrée de l'Erreur (Integral of Square Error).
Le critère de performance est alors le suivant :
e 2 ( ) (137)
t dt
0
En général, le fait de travailler avec le
carré de l'erreur amplifie l'importance des valeurs de sortie qui
s'écartent le plus de la valeur finale.
3- Critère ITAE, Intégrale de
l'Erreur Absolue pondérée par le Temps (Integral Time multiplied
by Absolute Error).
Le critère de performance est le suivant :
t
t t dt
e( ) (138)
ITAE j.

0
Puisque la valeur du critère ITAE est
pondérée par le temps, l'erreur statique est fortement
pénalisée : les systèmes à réponse
très oscillatoire sont ainsi pénalisés.
En règle générale, le système sera
d'autant mieux réglé que le critère intégral choisi
sera minimal.
4.3.3- Conclusion.
Le choix de critère de simulation le plus performant
(le bon critère) est délicat. Nous avons opté dans notre
travail pour les critères instantanés de préférence
aux critères intégraux de façon à faciliter la
comparaison avec les résultats de la littérature.
4.4- Développement de l'AG. 4.4.1-
Introduction.
Rappelons que les AGs sont des algorithmes d'optimisation
s'appuyant sur des techniques dérivées de la
génétique et de l'évolution naturelle avec trois
opérateurs : croisement, mutation et sélection. L'usage d'un AG
est d'une part adapté à une exploration rapide et globale d'un
espace de recherche de taille importante et d'autre part capable de fournir
plusieurs solutions. Un AG recherche le ou les extrema d'une fonction
définie (fonction objectif) sur un espace de recherche
définissant les contraintes des paramètres à optimiser.
Dans ce paragraphe nous présentons la formulation de la
fonction multiobjectif proposée et la mise en oeuvre de l'AG
utilisé.
4.4.2- Fonction objectif.
Le but de l'utilisation des PSSs est d'assurer un
amortissement satisfaisant des oscillations et de garantir la stabilité
globale du système pour différents points de fonctionnement. Pour
répondre à ce but, nous avons utilisé une fonction
multiobjectif composée de deux fonctions objectif. Cette fonction
multiobjectif doit maximiser la marge de stabilité en augmentant les
facteurs d'amortissement tout en minimisant les parties réelles des
valeurs propres du système. Par conséquent, toutes les valeurs
propres seront dans la zone D de stabilité.
Les étapes de calcul de cette fonction multiobjectif sont
les suivantes :
1- Formuler le système linéaire en boucle ouverte
(sans PSSs).
2- Positionner les PSSs avec leurs paramètres
initialisés par l'AG à travers une population initiale.
3- Fermer la boucle en reliant le
jème PSS entre la sortie du
jème générateur et son
entrée.
4- Calculer les valeurs propres du système en boucle
fermée et prendre uniquement les modes dominants dont le
ième mode se traduit par :
ë i = ó i #177; jù
i (139)
5- Trouver les parties réelles des valeurs propres du
système (ói) et calculer les facteurs d'amortissement
(æi) pour les ième modes:
æi
-ói
=
(140)
2 2
+ ù i
ó i
6- Déterminer la valeur minimale de (æi)
et la valeur maximale de (- ói), qui peuvent être
formulées respectivement comme : (minimum (æi))
et (? maximum (ói)).
7- Rassembler les deux fonctions objectif en une fonction
multiobjectif F comme suit (méthode de pondération) :
F = -max(ó i )+min(
æ i ) (141)
8- Renvoyer la valeur de cette fonction multiobjectif au
programme de l'AG pour relancer une nouvelle génération.
Dans notre cas, nous n'avons privilégié aucune
fonction objectif sur une autre : le coefficient de pondération de
chaque fonction individuelle est donc égal à 1.
4.4.3- Mise en oeuvre de l'AG. 4.4.3.1- Codage du
problème.
L'objectif de cette étude est d'appliquer l'AG pour
trouver :
- les valeurs optimales des paramètres des PSSs pour un
meilleur amortissement, - leur localisation optimale,
- le nombre suffisant des PSSs.
Ainsi, le nombre de variables utilisé (pour chaque PSS)
à l'entrée de l'AG variera selon trois cas étudiés
:
1- Premier cas : trois variables (un
gain et deux constantes de temps). L'objectif est simplement d'optimiser les
paramètres des PSSs.
2- Deuxième cas : quatre
variables (l'emplacement des PSSs, un gain et deux constantes de temps).
L'objectif maintenant est d'optimiser les paramètres des PSSs et leur
localisation.
3- Troisième cas : cinq
variables (un commutateur déterminant la mise en service ou non d'un
PSS, l'emplacement des PSSs, un gain et deux constantes de temps). L'objectif
est d'optimiser enfin les paramètres des PSSs et leur localisation et de
réduire leur nombre.
Ces variables sont soumises aux contraintes suivantes :
|
KPSS
|
, ,
j
|
min
|
= =
K K
PSS j PSS j
, , , max
|
T1
min
, ,
j
==
T T
max
1 , 1 , , j j
= =
T T
3 , 3 , , max
j j
{ }
Gen Gen
1 L , , n
{ }
0,1
(142)
T3
min
, ,
j
,
PLPSS
j
,
SWPSS
j
KPSS : le gain du PSS.
T1 : la constante de temps du PSS.
T3 : la constante de temps du PSS.
NPSS : le nombre maximum des PSSs à ajouter aux
générateurs.
PLPSS : le numéro de générateur
auquel le PSS doit être connecté. Sa valeur varie entre 53 et
68.
SWPSS : une variable représentant des
commutateurs permettant de relier (si la valeur est 1) ou débrancher (si
la valeur est 0) les PSSs des générateurs, afin d'en
réduire leur nombre.
Pour coder le problème, à Nvar
nombre de variables, chaque variable (chromosome) est représentée
par Sl chaîne de bits (Sl gène) de
longueur Ngens, où : l = 1, 2,..., Nvar.
A titre d'exemple, la figure (51) suivante montre une
configuration d'un individu, composée de cinq chromosomes,
représentant le troisième cas étudié.

1 1 0 1 ...
0 1 0 1 ...
0 0 0 1 ...
1 0 0 0 ...
0 1 1 1 ...
... 0 1
... 1 1
... 1 0
... 1 1
... 0 0
Constante de temps T3
Constante de temps T1
Gain KPSS
Commutateur SWPSS Emplacement
PLPSS
Figure 51. Représentation d'un
individu pour le troisième cas étudié.
Le type de codage choisi dans cette étude est le codage
binaire : il est standard et applicable pour plusieurs types de
problèmes.
4.4.3.2- Population initiale.
Les AGs nécessitent une population initiale pour
commencer le processus de recherche. La méthode appliquée fait
générer aléatoirement un ensemble de solutions dans les
contraintes proposées pour la population entière : c'est la
méthode la plus commune.
Une représentation d'une population initiale de
Nind individus (solutions) est illustrée par la
figure (52).
0 0 0 1 ...
0 1 1 1 ...
1 1 0 1 ...
0 0 1 1
0 1 0 1 ...
10 0 0 ...
0 0 0 1 ...
0 1 0 1 ...
1 0 0 0
0 1 1 1 ...
...
...
... 0 0
0
... 1 0
... 1 1
... 0 1
... 0 1
0 1
... 1 0
... 1 1
... 1 1
... 0 0
0 1
0 0
1
0
0
Figure 52. Représentation de la
population entière de Nind individus.
4.4.3.3- Sélection.
Après génération de la population
initiale, la performance de chaque individu est évaluée : la
performance mesure la qualité de la solution probable pour comparer les
différentes solutions. Nous avons pris la valeur associée
à la fonction objectif comme indice de performance.
Après calcul de cet indice pour chaque individu, le
mécanisme de sélection est appliqué pour copier les
individus sélectionnés. Les individus ayant des performances
élevées ont plus de probabilité d'être reproduits
dans la génération suivante. Nous avons appliqué la
méthode de la roulette biaisée.
4.4.3.4- Croisement.
Après l'étape de sélection, le croisement
est appliqué. Dans cette étape, les individus sont
regroupés aléatoirement par paire (parents). Le croisement se
fait ensuite pour créer les enfants avec une probabilité
Pc, sinon les parents ne changent pas. Cet opérateur
sert à explorer des nouvelles régions dans l'espace de recherche.
Le type de croisement le plus simple est le croisement seul point : nous
l'avons appliqué dans cette étude.
4.4.3.5- Mutation.
Pour introduire une certaine diversification dans la
population et éviter ainsi une convergence prématurée en
un optimum local, l'opérateur de mutation est appliqué. Les bits
subissent la mutation sont choisis aléatoirement avec une
probabilité Pm.
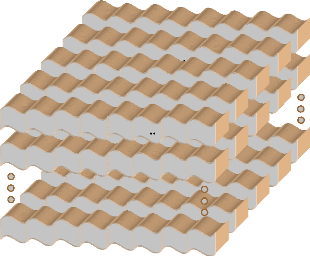
4.4.4- L'organigramme du problème.
Les étapes de la formulation de la fonction multiobjectif
et du programme de l'AG sont donnés à la figure (53).
4.4.5- Conclusion.
Dans les parties précédentes de ce chapitre,
nous avons décrit le réseau électrique
étudié dans ce travail et détaillé les
critères de la stabilité qui sont très nécessaires
pour évaluer concrètement nos résultats. Nous avons aussi
présenté la formulation de la fonction multiobjectif
proposée et les points de la mise en oeuvre de l'AG utilisé.
Dans la partie suivante, nous allons mettre en application nos
approches. Les résultats obtenus seront analysés et
discutés :
- Nous commençons avec l'analyse du système sans
l'utilisation des PSSs.
- Nous présentons, par la suite, les résultats
de l'application du premier cas destiné à optimiser les
paramètres des PSSs du système par l'AG. Nous comparons ces
résultats avec ceux déterminés par une méthode
classique (compensation de phase) et par une méthode
métaheuristique (algorithmes d'optimisation par essaim de particules) et
avec ceux fournis dans la littérature.
- Dans le deuxième et troisième cas, nous
optimisons l'emplacement et le nombre des PSSs. Les objectifs et les
intérêts de ces applications et leurs résultats seront
présentés et discutés.
Population initiale pour les
paramètres à
optimiser
Figure 53. Organigramme de la fonction
multiobjectif et du programme de l'AG.
Base de données du système
Ecoulement de puissance
Point de fonctionnement
Linéarisation du système
Valeurs propres
pour chaque individu :
ói, æi
Paramètre de réglage d'AG
La fonction multiobjectif
F = -max(ó i
)+min(æ i
)
Evaluation des solutions
Opérateurs d'AG :
(Sélection, Croisement,
Mutation)
Oui
Gener < Genermax ?
Non
Nouvelle population
Nouvelle génération
Résultat
4.5- Résultat et discussion. 4.5.1- Le
système sans PSSs.
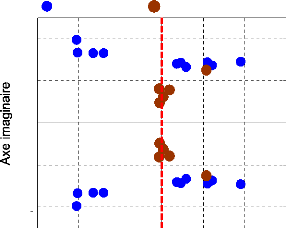
Nous étudions en premier lieu le fonctionnement du
système sans PSSs. Les modes électromécaniques dominants
du système pour le point de fonctionnement considéré sont
donnés dans le tableau (4) et à la figure (54).
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 0.4120#177; j 9.8436
|
0.0418
|
1.5667
|
|
2
|
- 0.0095#177; j 2.3974
|
0.0040
|
0.3816
|
|
3
|
+ 0.0063#177; j 3.1120
|
- 0.0020
|
0.4953
|
|
4
|
+ 0.0377#177; j 3.8959
|
- 0.0097
|
0.620 1
|
|
5
|
- 0.0116#177; j 4.0526
|
0.0029
|
0.6450
|
|
6
|
- 0.4056#177; j 8.3777
|
0.0484
|
1.3333
|
|
7
|
- 0.2814#177; j 8.2667
|
0.0340
|
1.3157
|
|
8
|
- 0.3295#177; j 8.2650
|
0.0398
|
1.3154
|
|
9
|
+ 0.2152#177; j 6.2618
|
- 0.0344
|
0.9966
|
|
10
|
+ 0.1188#177; j 6.6535
|
- 0.0178
|
1.0589
|
|
11
|
+ 0.3803#177; j 7.3056
|
- 0.0520
|
1.1627
|
|
12
|
+ 0.2420#177; j 6.8133
|
- 0.0355
|
1.0844
|
|
13
|
+ 0.0919#177; j 7.1486
|
- 0.0129
|
1.1377
|
|
14
|
+ 0.2216#177; j 7.2291
|
- 0.0306
|
1.1506
|
|
15
|
+ 0.0717#177; j 7.0438
|
- 0.0102
|
1.1211
|
Tableau 4. Valeurs propres du
système sans PSSs.
10
5
0
-5
-10
Modes locaux Modes interrégionaux
-0.6 -0.4 -0.2 0.2 0.4 0.6
0
Axe réel
Figure 54. Répartition des valeurs
propres du système dans le plan complexe (sans PSSs).
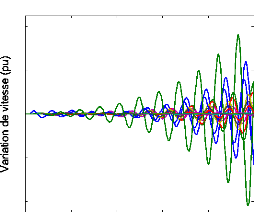
Nous appliquons maintenant une petite perturbation
normalisée en échelon de 1% sur le couple mécanique du
générateur 53. La variation de vitesse des
générateurs qui fait suite à cette perturbation est
montrée à la figure (55).
x 10-3
8
4
0
-4
-8
0 2 4 6 8 10
Temps (s)
Figure 55. Variation de vitesse des
générateurs (sans PSSs).
Ainsi, il est évident que le système contient
des modes instables (en gras dans le tableau (4)) et d'autres mal amortis. Le
comportement du système aux petites perturbations montre clairement
cette instabilité du système (divergence de l'ensemble des
générateurs).
La présence de modes d'oscillations
électromécaniques fortement instables déterminés
par l'analyse de la réponse du système en modèle
linéaire conduit évidemment à la perte de stabilité
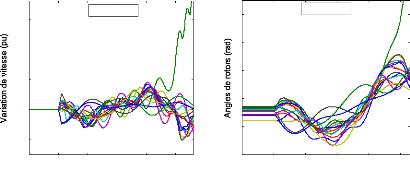
aux grandes perturbations. Nous appliquons un défaut triphasé sur
la ligne (59#23) suivi par une élimination du défaut. Le temps de
défaut et de retour à l'état initial est choisi de l'ordre
de 6 périodes du réseau (0.1 s). Les réponses temporelles
de la variation de vitesse et des angles de rotor des générateurs
suite au défaut choisi sont montrées à la figure (56).
8
0.06
sans PSSs
6
sans PSSs
0.04
4
0.02
2
0
0
-0.02
0 1 2 3 4 5
Temps (s)
-2 0 1 2 3 4 5
Temps (s)
a b
Figure 56. Réponse dynamique des
générateurs (sans PSSs)
a : variation de
vitesse, b : angles de rotor.
Cette figure montre bien que les modes instables mènent
à un écart croissant apériodique de certains angles de
rotor et par conséquent à la perte de la stabilité du
système.
Pour rétablir la stabilité du système et
améliorer son amortissement global, les PSSs sont maintenant
ajoutés aux générateurs. Dans la suite de ce chapitre,
nous faisons appel aux AGs pour optimiser les paramètres des PSSs selon
les trois cas présentés précédemment.
4.5.2- Les scénarios et
défauts.
Pour analyser la performance et la robustesse du
réglage, nous devons analyser les nouvelles valeurs propres du
système et examiner l'amortissement obtenu avec les PSSs
optimisés pour différents scénarios crédibles,
tableau (5). Nous allons appliquer ces analyses au point de fonctionnement
nominal utilisé pour l'optimisation (noté premier
scénario) et pour deux autres points représentant deux
scénarios sévères. En effet, le deuxième et
troisième scénario, définis ci-dessus, sont
déterminés à partir des simulations que nous avons
réalisées et représentent les contraintes les plus dures
pour le système :
- Le scénario deux peut être
considéré comme un scénario sévère car les
lignes d'interconnexion (8#9) et (46#49) participent fortement aux oscillations
interrégionales et la perte de ces deux lignes va affaiblir
considérablement les interconnexions entre les régions du
système.
- Le scénario trois est aussi un scénario
sévère. Il correspond à une diminution de puissance du
générateur 68 associée à une augmentation de la
charge connectée au jeu de barre 37. Or le générateur 68 a
une puissance importante et la charge connectée au jeu de barre 37
consomme la puissance la plus grande du réseau. Enfin, ce
scénario implique la perte de la ligne (2#3).

N° scénario
1
2
Configuration de scénario
Point de fonctionnement nominal
- Ligne 8#9 hors service
- Ligne 46#49 hors service
- Diminution 25% de la puissance active du
générateur 16
3 - Augmentation 25% de la puissance active de
la charge au jeu de barre 37
- Ligne 2#3 hors service
Tableau 5. Liste des scénarios
proposés.
Jusqu'à maintenant, l'analyse de réglage est
basée seulement sur le modèle linéaire du système.
Etant donné que le modèle d'origine est non-linéaire, nous
devons évaluer la performance et la robustesse du réglage des
PSSs en considérant le modèle non-linéaire originel. Pour
ce faire, nous effectuons des simulations temporelles du système pour
ces différents scénarios en présence d'une perturbation
transitoire sévère déduite de simulations. Cette
perturbation sévère correspondant à un défaut
triphasé sur la ligne (59#23) est appliquée à
proximité du jeu de barre 59 ; il est suivi par une ouverture des
disjoncteurs et une fermeture de la ligne après élimination du
défaut. Le temps de défaut et de retour à l'état
initial est choisi de l'ordre de 6 périodes du réseau (0.1 s).
4.5.3- Cas 1 : optimisation des paramètres des
PSSs.
Dans la suite de ce paragraphe, nous présentons les
étapes habituelles de l'optimisation des paramètres des PSSs,
à savoir :
- Détermination de la meilleure localisation des PSSs. La
méthode utilisée pour
déterminer cette implantation est la méthode des
facteurs de participation.
- Optimisation des valeurs des paramètres des PSSs,
déjà installés dans le système. La
méthode d'optimisation utilisée est les AGs.
- Vérification de la performance et de la robustesse
correspondant au réglage effectué pour différents
scénarios. Pour ce faire, nous utilisons l'analyse par valeurs propres
et l'évaluation temporelles des performances par simulations
dynamiques.
4.5.3.1- Localisation des PSSs.
La méthode des facteurs de participation nous permet de
déterminer les générateurs participants à chaque
mode critique. Les générateurs présentant les valeurs de
participation les plus élevées sont ceux qui nécessitent
d'être équipés en priorité de PSSs. Les
résultats sont donnés dans le tableau (6) : 14
générateurs participent principalement à ces modes. La
fréquence de chaque mode et les générateurs
associés déterminent le type du mode. Nous avons ainsi quatre
modes de type interrégional et onze modes de type local.
|
N° mode
|
ë
|
f [Hz]
|
Générateurs participants
|
Type de mode
|
|
1
|
- 0.4120#177; j 9.8436
|
1.5667
|
G. 63
|
Local
|
|
2
|
- 0.0095#177; j 2.3974
|
0.3816
|
G. 65, G. 67, G. 66
|
Interrégional
|
|
3
|
0.0063#177; j 3.1120
|
0.4953
|
G. 68, G. 66
|
Interrégional
|
|
4
|
0.0377#177; j 3.8959
|
0.6201
|
G. 65, G. 58, G. 57
|
Interrégional
|
|
5
|
- 0.0116#177; j 4.0526
|
0.6450
|
G. 67, G. 66, G.68
|
Interrégional
|
|
6
|
- 0.4056#177; j 8.3777
|
1.3333
|
G. 56
|
Local
|
|
7
|
- 0.2814#177; j 8.2667
|
1.3175
|
G. 60
|
Local
|
|
8
|
- 0.3295#177; j 8.2650
|
1.3154
|
G. 59
|
Local
|
|
9
|
0.2152#177; j 6.2618
|
0.9996
|
G. 64
|
Local
|
|
10
|
0.1188#177; j 6.6535
|
1.0589
|
G. 57
|
Local
|
|
11
|
0.3803#177; j 7.3056
|
1.1627
|
G. 61
|
Local
|
|
12
|
0.2420#177; j 6.8133
|
1.0844
|
G. 54
|
Local
|
|
13
|
0.0919#177; j 7.1486
|
1.1377
|
G. 58
|
Local
|
|
14
|
0.2216#177; j 7.2291
|
1.1506
|
G. 55
|
Local
|
|
15
|
0.0717#177; j 7.0438
|
1.1211
|
G. 62
|
Local
|
Tableau 6. Générateurs
participants aux modes critiques.
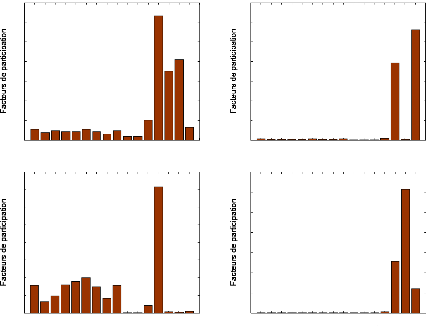
L'analyse des facteurs de participation montre l'influence de
chaque générateur dans le mode en question. Si la participation
d'un générateur est relativement faible, le placement d'un PSS
sur ce générateur n'apportera que peu d'amélioration. Les
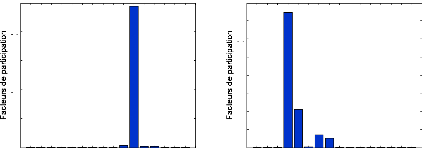
figures (57) et (58) montrent les facteurs de participation associés aux
angles et aux variations de vitesse de chaque générateur pour les
quatre modes interrégionaux (les modes 2, 3, 4 et 5) et pour deux modes
locaux (modes 1 et 6).
La méthode des facteurs de participation détermine
donc 14 générateurs devant être équipés des
PSSs. Ce sont les suivants :
|
G. 54
|
G. 55
|
G. 56
|
G. 57
|
G. 58
|
G. 59
|
G. 60
|
|
G. 61
|
G. 62
|
G. 63
|
G. 64
|
G. 65
|
G. 67
|
G. 68
|
Le réglage des paramètres de ces PSSs fait l'objet
du paragraphe suivant.
Numéro de générateur
Numéro de générateur
0.7
Mode 2
Mode 3
0.3
0.6
0.25
0.5
0.2
0.4
0.15
0.3
0.1
0.2
0.1
0.05
0
0
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
Numéro de générateur
Numéro de générateur
0.7
0.4
Mode 4
Mode 5
0.35
0.6
0.3
0.5
0.25
0.4
0.2
0.3
0.15
0.2
0.1
0.1
0.05
0
0
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
Figure 57. Facteurs de participation des
modes interrégionaux (modes 2, 3, 4 et 5).
Numéro de générateur Numéro de
générateur
0.8
0.6
0.4
0.2
0
1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
Mode 1
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
Mode 6
Figure 58. Facteurs de participation de
deux modes locaux (modes 1 et 6).
4.5.3.2- Réglage des paramètres des PSSs
par l'AG.
Nous utilisons les AGs pour optimiser simultanément le
réglage des paramètres des PSSs en se basant sur le modèle
linéaire du système. L'objectif de ce réglage
simultané est d'évaluer l'amortissement de tout le système
et de minimiser les possibles interactions défavorables entre les PSSs.
Pour atteindre cet objectif, les valeurs propres du système doivent,
comme nous l'avons vu, se placer dans la zone D de
stabilité.
Ainsi, l'AG appliqué doit maximiser les valeurs fournies
par la fonction multiobjectif du système. Pour le cas
étudié, le problème d'optimisation est alors
formulé comme suit :
OptAG max( max( i ) min(
i ))
= - ó + æ (143)
La figure (59) donne une représentation graphique de cette
procédure d'optimisation cordonnée.
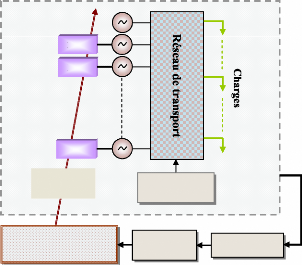
Algorithme génétique
Paramètres
des PSSs
PSS 14
PSS 1
PSS 2
G16
G2
G3
G1
Fonction
multiobjectif
Point de
fonctionnement
Valeurs propres
Figure 59. Optimisation coordonnée
des paramètres des PSSs.
Les trois paramètres à optimiser pour chaque PSS
(un gain et deux constantes de temps) sont soumises aux contraintes suivantes
:
|
0.1 40
= =
K PSS j
,
0 . 00 1 0 . 1
= =
T 1 , j
0 . 00 1 0 . 1
= =
T 3 , j
|
(144)
|
|
avec
|
j
|
1,2,
|
|
, NPSS
|
Les autres paramètres (Tw,j
et T2,j, T4,j) des PSSs sont considérés
constants : Tw,j = 10 et T2,j = T4,j = 0.02.
Le tableau (7) donne les valeurs choisies des paramètres
de l'AG.
|
Nombre d'individu Nind
|
75
|
|
Nombre de gènes Ngens
|
Nind x Nvar
|
|
Nombre de génération Ngener
|
250
|
|
Probabilité de croisement Pc
|
0.9
|
|
Probabilité de mutation Pm
|
0.005
|
Tableau 7. Valeurs choisies des
paramètres de l'AG.
La figure (60) montre la convergence des paramètres des
PSSs (KPSSi, T1i et T3i) vers
leurs valeurs optimales. Pendant les premières
générations, les valeurs de ces paramètres (les individus)
sont réparties sur la quasi-totalité de leurs espaces de
recherche. Au fur et à mesure de la progression des
générations, les individus (de chaque paramètre)
s'orientent et convergent enfin vers leurs valeurs optimales. Ces
dernières sont données dans le tableau (8).

a
b c
Figure 60. Convergence de la population
des paramètres des PSSs (a : KPSSi, b
: T1i, c : T3i).
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
54
|
35.2115
|
0.0543
|
0.0484
|
|
2
|
55
|
21.4336
|
0.0222
|
0.0424
|
|
3
|
56
|
33.4921
|
0.0665
|
0.0981
|
|
4
|
57
|
30.7770
|
0.0309
|
0.0469
|
|
5
|
58
|
35.8410
|
0.0901
|
0.0796
|
|
6
|
59
|
23.3611
|
0.0511
|
0.0377
|
|
7
|
60
|
01.5493
|
0.0829
|
0.0798
|
|
8
|
61
|
12.7207
|
0.0067
|
0.0309
|
|
9
|
62
|
30.1377
|
0.0882
|
0.0749
|
|
10
|
63
|
13.9789
|
0.0518
|
0.0754
|
|
11
|
64
|
38.7296
|
0.0598
|
0.0908
|
|
12
|
65
|
15.1873
|
0.0266
|
0.0081
|
|
13
|
67
|
39.9831
|
0.0012
|
0.0015
|
|
14
|
68
|
32.3178
|
0.0010
|
0.0010
|
Tableau 8. Paramètres des PSSs
optimisés par AG.
L'évolution de la fonction multiobjectif en fonction du
nombre de générations est donnée à la figure (61) ;
la valeur finale atteinte pour la génération maximale
prédéterminée de 250 est de 1.097. Les évolutions
des deux composantes (æ et ó) de la fonction
multiobjectif sont données quant à elles à la figure (62).
Nous remarquons sur cette dernière que la valeur minimale optimale de
(æ) et la valeur maximale optimale de (ó) sont
atteintes pour la génération maximale
prédéterminée de 250.
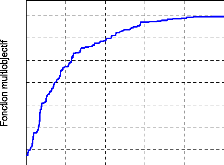
1.1
1
0.9
0.8
0.7
0.6
0.5
0 50 100 150 200 250
Générations
Figure 61. Evolution de la fonction
multiobjectif.
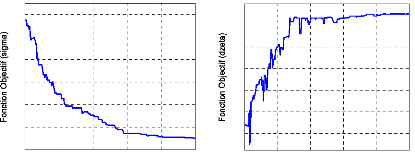
0.16
-0.4
0.14
-0.5
0.12
-0.6
0.1
-0.7
0.08
-0.8
0.06
-0.9
0.04
0 50 100 150 200 250
Générations
0 50 100 150 200 250
Générations
-1
a b
Figure 62. Evolutions des composantes de
la fonction multiobjectif (a : æ, b :
ó).
4.5.3.3- Analyse des valeurs propres. 4.5.3.3.1- Le
point de fonctionnement nominal.
Les valeurs propres du système, équipé de
ces 14 PSSs, et leur répartition dans le plan complexe sont
données respectivement dans le tableau (9) et à la figure
(63).
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 7.5602 #177; j 14.579
|
0.4603
|
2.3203
|
|
2
|
- 2.4631 #177; j 13.726
|
0.1766
|
2.1847
|
|
3
|
- 9.1765 #177; j 10.153
|
0.6705
|
1.6160
|
|
4
|
- 9.5284 #177; j 6.6435
|
0.8203
|
1.0573
|
|
5
|
- 1.9641 #177; j 9.1431
|
0.2100
|
1.4552
|
|
6
|
- 1.0945 #177; j 7.2031
|
0.1502
|
1.1464
|
|
7
|
- 1.0897 #177; j 7.1452
|
0.1508
|
1.1372
|
|
8
|
- 3.5594 #177; j 5.5850
|
0.5375
|
0.8889
|
|
9
|
- 5.6561 #177; j 3.9954
|
0.8 168
|
0.6359
|
|
10
|
- 3.7923 #177; j 4.4182
|
0.65 13
|
0.7032
|
|
11
|
- 4.2798 #177; j 3.1753
|
0.8031
|
0.5054
|
|
12
|
- 0.9485 #177; j 3.8260
|
0.2406
|
0.6089
|
|
13
|
- 1.1258 #177; j 3.3302
|
0.3203
|
0.5300
|
|
14
|
- 0.9560 #177; j 2.9392
|
0.3093
|
0.4678
|
|
15
|
- 1.3365 #177; j 2.6372
|
0.4521
|
0.4197
|
Tableau 9. Valeurs propres du
système (14 PSSs optimisés par AG).
D'après l'analyse des valeurs propres du
système, nous trouvons que le facteur d'amortissement minimum est
æmin = 15.02 % et que la partie réelle maximale des
valeurs propres est ómax = - 0.9485.
Nous pouvons remarquer que les modes
électromécaniques (locaux et interrégionaux) ont
été décalés dans la zone D de
stabilité du plan complexe. Il apparaît deux valeurs propres
situées juste à l'extérieur de la zone D : les
valeurs obtenues restent néanmoins très proches de la limite de
zone. Elles conservent en outre une excellente marge de stabilité
absolue. Enfin, elles correspondent à des facteurs d'amortissement
très supérieurs au critère que nous avions
précédemment défini.
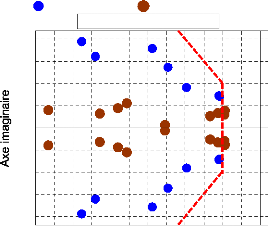
1er cas , 1er scénario
20
dz = 10 %
10
0
-10
-20
-6 -5 -4 -3 -2 - 0
-1
Modes locaux Modes interrégionaux
Axe réel
Figure 63. Répartition des valeurs
propres du système dans le plan complexe
(14 PSSs optimisés
par AG).
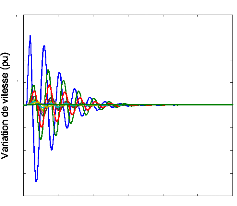
La variation de vitesse des générateurs qui fait
suite à une petite perturbation en échelon de 1% sur le couple
mécanique du générateur 53 est présentée
à la figure (64).
4x 10-4
3
2
1
0
-1
-2
-3
-4 0 2 4 6 8 10 12
Temps (s)
Figure 64. Variation de vitesse des
générateurs.
Ces résultats confirment que le système est bien
évidemment stable aux petites perturbations.
Nous allons dans la suite de ce paragraphe comparer le
résultat obtenu par l'AG avec ceux déterminés :
- par une méthode classique,
- par une méthode métaheuristique,
- dans la littérature.
La méthode classique choisie est la
méthode de compensation de phase. Nous appliquons cette
méthode pour un réglage séquentiel des 14 PSSs,
localisés par la méthode des FP, sur la base des étapes
expliquées dans le paragraphe (§§-2.4.5.2.1). Le premier PSS
est réglé en utilisant le résultat de l'analyse des
valeurs propres en boucle ouverte. Les valeurs propres du système en
boucle fermée utilisant le premier PSS sont calculées et
utilisés dans le réglage du deuxième PSS. Cette
procédure s'applique pour les autres PSSs et, à chaque
étape de ce réglage séquentiel, le modèle du
système est mis à jour avec les PSSs ajoutés
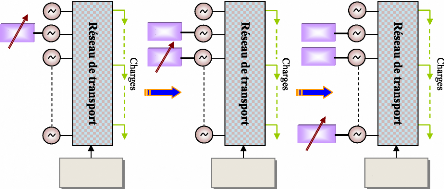
précédemment. La figure (65) donne une représentation
graphique de cette procédure séquentielle.
G2
G2
PSS1
PSS1
PSS1
G3
G3
PSS2
PSS2
G16
G16
PSS14
G1
Point de
fonctionnement
G1
G2
G3
G16
G1
Point de
fonctionnement
Point de
fonctionnement
Figure 65. Réglage
séquentiel des paramètres des PSSs.
Les valeurs des paramètres de réglage des PSSs
déterminés par cette méthode sont données en annexe
D.
Les valeurs propres du système, avec les 14 PSSs, sont
données dans le tableau (10) ; leur répartition dans le plan
complexe est montrée graphiquement à la figure (66).
Ces résultats montrent que le système est devenu
stable pour le point de fonctionnement étudié, mais plusieurs
modes ne se trouvent pas dans la zone D ; un mode
(ë14) reste encore mal amorti.
Ce résultat s'interprète en tenant compte du fait
que les méthodes classiques ne prennent pas en compte les interactions
entre PSSs et que leur réglage se fait sans coordination.
L'analyse comparative des résultats obtenus par ces
méthodes montre donc la supériorité de l'utilisation de
l'AG.
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 3.8969 #177; j 13.710
|
0.2734
|
2.1821
|
|
2
|
- 4.6589 #177; j 13.268
|
0.3313
|
2.1118
|
|
3
|
- 3.3208 #177; j 7.9161
|
0.3868
|
1.2599
|
|
4
|
- 0.2396 #177; j 7.1521
|
0.0335
|
1.1383
|
|
5
|
- 2.8883 #177; j 6.7292
|
0.3944
|
1.0710
|
|
6
|
- 1.1655 #177; j 6.7009
|
0.1714
|
1.0665
|
|
7
|
- 2.7053#177; j 6.5937
|
0.3796
|
1.0494
|
|
8
|
- 1.2536 #177; j 6.1625
|
0.1993
|
0.9808
|
|
9
|
- 1.6629 #177; j 6.5117
|
0.2474
|
1.0364
|
|
10
|
- 2.1114 #177; j 6.1520
|
0.3246
|
0.9791
|
|
11
|
- 1.8371 #177; j 6.1483
|
0.2863
|
0.9785
|
|
12
|
- 0.8886 #177; j 3.7589
|
0.2301
|
0.5982
|
|
13
|
- 0.6306 #177; j 3.6811
|
0.1688
|
0.5859
|
|
14
|
- 0.3772 #177; j 3.1160
|
0.1202
|
0.4959
|
|
15
|
- 0.7242#177; j 2.27830
|
0.3029
|
0.3626
|
Tableau 10. Valeurs propres du
système
(14 PSSs réglés par la méthode de
compensation de phase).
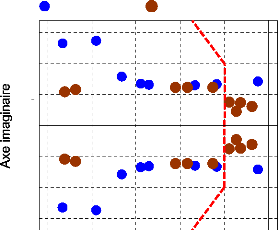
15
10
5
0
-5
-10
-15
dz = 10 %
Modes locaux Modes interrégionaux
-5 -4 -3 -2 - 0
-1
Axe réel
Figure 66. Répartition des valeurs
propres du système dans le plan complexe
(14 PSSs
réglés par la méthode de compensation de phase).
Les méthodes métaheuristiques d'optimisation
sont, comme nous l'avons déjà cité, nombreuses. Une de ces
méthodes est les algorithmes d'optimisation par essaim de particules,
(AOEP), (Particle Swarm Optimisation). Ces derniers ont été
introduits par Kennedy et Eberhart (Kennedy et al., 1995) en 1995. Ces
algorithmes sont une technique stochastique d'optimisation inspirés des
mouvements coordonnés des oiseaux en nuées ou des bancs de
poissons (Kennedy et al., 2001; Bonabeau et al., 2002). Les
AOEP, comme les algorithmes évolutionnaires, sont des méthodes
d'optimisation à population dont l'individu (particule)
représente une solution potentielle. Les AOEP partagent avec les AGs
plusieurs points communs tels que la génération aléatoire
de la population initiale et l'évolution des individus par
itérations en convergeant graduellement vers la solution optimale.
Chaque particule vole dans l'espace de recherche du
problème avec une vitesse adaptative qui se modifie dynamiquement selon
sa propre expérience du vol et l'expérience du vol des autres
particules. Ainsi, chaque particule essaie de s'améliorer en suivant le
chemin de son meilleur voisin. En outre, chaque particule possède une
mémoire qui lui permet de se rappeler de la meilleure position qu'elle
avait visitée dans l'espace de recherche. La position de la particule
correspondante à la meilleure performance est appelée
pbest et la meilleure position de toutes les particules est
appelée gbest.
L'évolution de la vitesse et la position de chaque
particule peuvent être calculées en utilisant les informations de
sa vitesse actuelle et de la distance entre sa position actuelle et les
positions pbesti et gbest, comme les donnent les relations
suivantes (Bonabeau et al., 2002; Kwang et al., 2008) :
|
v w v c rand pbest x c rand gbest x
k + 1 k k
= · + · · - + · · -
1 1 ( ) 2 2 (
k
i i i i i
|
) (145)
|
x x v k i np
k + = + + = K
1 1
k ; 1,2, , (146)
i i i
|
w w
= max
|
w w
max min
-
itermax
|
iter
|
(147)
|
Avec :
vi k : vitesse actuelle de la
ième particule à la
kème itération.
w : fonction de pondération.
c1, c2 : coefficients de pondération.
rand : nombre aléatoire entre 0 et 1.
xi k : position actuelle de la
ième particule à la
kème itération.
pbesti : pbest de la
ième particule. gbest : gbest de la
population.
np : nombre des particules dans la population.
wmax : poids maximum.
wmin : poids minimum.
iter : nombre actuel d'itérations. itermax
: nombre maximum d'itérations.
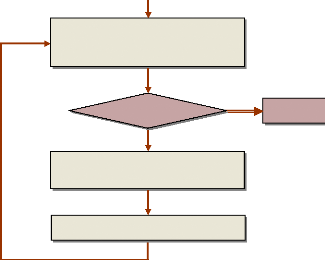
L'organigramme général des AOEP peut être
illustré comme suit :
Population initiale des particules
Résultat
Evaluation de la performance de
chaque particule dans
l'actuelle
itération
Non
Gener < Genermax ?
Oui
Modification de la vitesse et
de la position de chaque
particule
Nouvelle itération
Figure 67. Organigramme
général des AOEP.
Nous appliquons le programme d'AOEP que nous avons
développé pour optimiser les 14 PSSs du système. Nous
utilisons le même espace de recherche proposé pour l'optimisation
par l'AG (relation (144)). Les valeurs choisies des paramètres de l'AOEP
et les valeurs optimales des paramètres des PSSs sont données en
annexe E.
La figure (68) décrit l'évolution de la fonction
multiobjectif en fonction du nombre de générations ; la valeur de
la fonction multiobjectif atteinte est de 1.075.
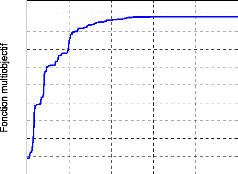
1.1
0.9
0.7
0.5
0.3
0 50 100 150 200 250
Générations
Figure 68. Evolution de la fonction
multiobjectif.
La répartition des valeurs propres du système est
donnée à la figure (69).
Modes locaux Modes interrégionaux


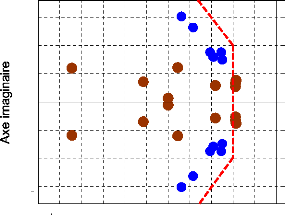
dz = 10 %
5
0
-5
-10
-15
-5 -4 -3 -2 -1 0
-1
15
10
Axe réel
Figure 69. Répartition des valeurs
propres du système dans le plan complexe
(14 PSSs optimisés
par AOEP).
L'analyse de ces valeurs montre que plusieurs d'entre elles se
trouvent hors de la zone D : le facteur d'amortissement minimum est
æmin = 14.32 % et la partie réelle maximale des valeurs
propres est ómax = - 0.93 17.
La comparaison avec les résultats obtenus par l'AG montre
que les résultats obtenus par l'AOEP sont inférieurs.
En effet, si les AOEP sont simples dans leur concept et
faciles à mettre en oeuvre par rapport à un AG car ils n'ont pas
d'opérateurs génétiques. Contrairement aux AGs, la
performance d'un AOEP dépend fortement de ses paramètres de
réglage. En outre, les AOEP risquent souvent d'être
piégés dans des optima locaux (Angeline, 1998; Xiao et
al., 2003).
Enfin, en ce qui concerne les résultats de la
littérature obtenus à l'aide des AGs, de nombreuses recherches
sur l'optimisation des paramètres des PSSs du réseau New
England/New York ont été effectuées. K. Hongesombut, par
exemple, a publié plusieurs articles (Hongesombut et al., 2001;
Hongesombut et al., 2002; Hongesombut et al., 2004;
Hongesombut et al., 2005) concernant ce problème. Dans la
référence (Hongesombut et al., 2005), les auteurs
présentent une méthode d'optimisation des PSSs utilisant une
combinaison entre un algorithme génétique hiérarchique et
un micro algorithme génétique parallèle.
Nous donnons ci-dessous les principes de ces deux algorithmes.
- Algorithme génétique hiérarchique (AGIT).
Dans un AG typique, la structure d'un chromosome est
prédéfinie et fixe ; le chromosome consistant en une chaîne
de gènes. Par contre, un chromosome d'un AGH est construit d'une
façon hiérarchique à partir de deux types
de gènes : les gènes de contrôle et les gènes de
paramètres. Les gènes de contrôle gouvernent l'état
d'activation des gènes de paramètres. Les autres gènes
sont responsables de l'optimisation des paramètres des PSSs.
- Micro algorithme génétique
parallèle (MAGP).
Lorsqu'on veut utiliser une population de petite taille, il y
a un risque que l'AG converge vers un optimum local. Ainsi, un AG typique peut
ne pas donner le résultat désiré avec une petite
population. Ceci est dû à l'insuffisance de diversité dans
le bassin de la population qui ne permet pas toujours d'éviter le
piège des optima locaux. Par contre, le MAGP se base sur l'utilisation
de multiples sous-populations. Ces dernières évoluent
indépendamment pour un certain nombre de générations.
Ensuite un processus de migration est appliqué en distribuant le
meilleur individu parmi les sous-populations. Le schéma de migration
fournit la diversité génétique demandée en
échangeant les informations entre les sous-populations.
Avec cette méthode, la stabilité globale du
système est assurée avec un facteur d'amortissement minimum
æmin = 15 % et une partie réelle maximale des valeurs
propres ómax = - 1. Ces résultats sont bien en accord
avec ceux que nous avons obtenus, mais avec un PSS de moins dans notre
étude (14 au lieu de 15 PSSs).
4.5.3.3.2- Les autres
scénarios.
Dans le paragraphe précédent, nous avons
examiné la performance de régulation pour le point de
fonctionnement nominal. Nous examinons ci-dessous cette performance
vis-à-vis des deux autres scénarios proposés.
Les représentations graphiques dans le plan complexe des
valeurs propres des deuxième et troisième scénarios sont
données respectivement à la figure (70).
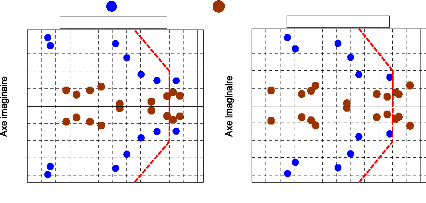
20
20
dz = 10 %
dz = 10 %
10
10
0
0
-10
-20
-6 -5 -4 -3 -2 - 0
-1
Axe réel
-10
-20
-6 -5 -4 -3 -2 - 0
-1
Axe réel
Modes locaux Modes interrégionaux
1er cas , 2ème scénario
1er cas , 3ème scénario
a b
Figure 70. Valeurs propres du
système pour le 1er cas,
a :
2ème scénario, b :
3ème scénario.
Les valeurs minimales de (æ) et maximales de
(ó) des deux scénarios sont données
respectivement comme suit :
|
æmin
|
ómax
|
|
Scénario 2
|
10.57 %
|
- 0.6284
|
|
Scénario 3
|
6.450 %
|
- 0.3743
|
Nous remarquons que la valeur critique du facteur
d'amortissement est bien respectée dans le deuxième
scénario mais pas pour le troisième, tandis que la valeur
critique de la partie réelle des valeurs propres n'est pas
respectée pour les deux autres scénarios. La figure (70) montre
que trois modes, pour chaque scénario, se trouvent en dehors de la zone
D de stabilité. Les caractéristiques correspondantes de
ces modes sont données dans le tableau suivant :
|
N° mode
|
ë
|
æ
|
f [Hz]
|
Type de mode
|
|
2ème
scénario
|
1
|
- 0.8603#177; j3.9143
|
0.2147
|
0.6230
|
Interrégional
|
|
2
|
0.6284#177; j 2.9158
|
0.2107
|
0.4641
|
Interrégional
|
|
3
|
- 0.7652#177; j 7.2000
|
0.1057
|
1.1459
|
Local
|
|
3ème
scénario
|
1
|
- 0.8820#177; j 3.7928
|
0.2265
|
0.603 6
|
Interrégional
|
|
2
|
0.7794#177; j 3.2443
|
0.2336
|
0.5163
|
Interrégional
|
|
3
|
- 0.3743#177; j 5.7897
|
0.0645
|
0.9212
|
Interrégional
|
Ce tableau montre que les modes se trouvant en dehors de la
zone D sont bien deux modes interrégionaux (le
3ème est local) pour le 2ème
scénario et trois modes pour le 3ème scénario. Par
conséquent, les modes interrégionaux sont les plus critiques.
4.5.3.4- Analyse par simulations temporelles.
4.5.3.4.1- Le point de fonctionnement nominal.
Pour compléter les informations sur les performances de
régulation obtenues avec le modèle linéaire, des
simulations temporelles du modèle non-linéaire sont, comme nous
l'avons expliqué au paragraphe (§§-4.3), nécessaires.
Nous devons ainsi examiner la restauration de la stabilité du
système pour les trois scénarios proposés suite à
un court-circuit triphasé sur la ligne 59#23. Nous traitons dans ce
paragraphe le point de fonctionnement nominal.
La figure (71) montre la variation de vitesse des cinq
générateurs les plus affectés par ce défaut. Ces
générateurs sont G.53, G.59, G.60, G.66 et G.68 ; ils
appartiennent à des régions différentes.
Les valeurs du dépassement maximum et du temps de
réponse mesurés sur ces courbes sont donnés dans le
tableau suivant.
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
Dp
|
5.48×10-3
|
10.6×10-3
|
5.01×10-3
|
- 9.84×10-3
|
0.49×10-3
|
|
tr (s)
|
7
|
7
|
8
|
8
|
8
|
Ainsi, nous constatons que le système est stable et les
oscillations s'amortissent en moins de 10 secondes.
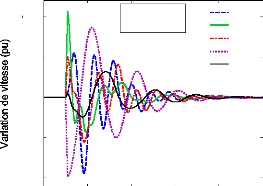
0.005
0.01
1er cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0
-0.005
-0.01
0 2 4 6 8 10
Temps (s)
Figure 71. Variations de vitesse des cinq
générateurs suite à un défaut de
ligne,
(1er scénario du 1er cas).
D'autres grandeurs physiques peuvent aussi être
simulées tels les angles de rotor, les puissances électriques et
les tensions de noeuds.
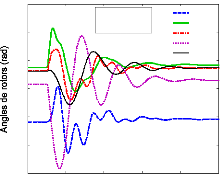
Les réponses temporelles des angles de rotor, avec le
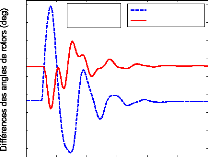
défaut proposé, sont montrées à la figure (72). Les
écarts entre les angles des générateurs 60 et 66 et les
écarts entre les angles des générateurs 68 et 53 sont
calculés à chaque instant : ils sont représentés
à la figure (73). Ces générateurs participent aux modes
interrégionaux ; appartenant à des régions
différentes, ils oscillent en opposition de phase comme l'illustre les
premières oscillations de la figure (73).
2.5
1.5
2
1er cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
1
0.5
0
-0.5 0 2 4 6 8 10
Temps (s)
Figure 72. Réponse dynamique des
angles de rotor des générateurs (1er scénario
du 1er cas).
120
100
1er cas,
1er scénario
(G. 60 - G. 66)
(G. 68 - G. 53)
80
60
40
20
0
-20
-40
0 2 4 6 8 10 12
Temps (s)
Figure 73. Réponse dynamique des
écarts des angles de deux paires des
générateurs,
(1er scénario du 1er
cas).
Nous remarquons que l'écart des angles de chaque paire
converge généralement au bout de 8 secondes.
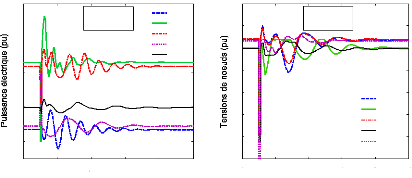
Les variations des angles des rotors influencent fortement les
puissances électriques des générateurs du système
ainsi que les tensions de noeuds. La figure (74) illustre la réponse
dynamique des puissances électriques des cinq générateurs
choisis et la réponse dynamique des tensions de quelques noeuds. Nous
avons choisi les noeuds de la ligne d'interconnexion 52#42, les noeuds de la
ligne 40#48 et le noeud 59 où le défaut était
appliqué.
1.6
1.4
1.2
1er cas,
1er scénario
G. 53
G. 59
G. 60
G. 63
G. 66
1.2
1
1er cas,
1er scénario
0.8
0.8
0.6
0.4
0
0.4
0.2
Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59
0 2 4 6 8 10
Temps (s)
00 2 4 6 8 10
Temps (s)
a b
Figure 74. Réponse dynamique du
système (1er scénario du 1er
cas),
a : puissances électriques, b
: tensions des noeuds.
Les courbes de ces deux figures confirment la restauration de
la stabilité du système lors d'un défaut de ligne, pour le
point de fonctionnement nominal. L'examen de la réponse dynamique du
système pour d'autres scénarios va être discuté dans
le paragraphe suivant.
4.5.3.4.2- Les autres
scénarios.
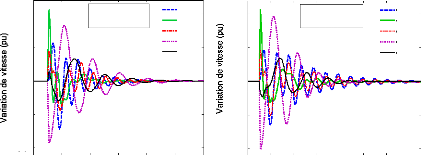
La figure (75) montre la variation de vitesse des cinq
générateurs pour les scénarios 2 et 3.
|
0 2 4 6 8 10 12
Temps (s)
|
0 2 4 6 8 10 12 14
Temps (s)
|
a b
-0.005
0.005
-0.01
0.01
0
1er cas,
2ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
-0.005
0.005
-0.01
0.01
0
1er cas,
3ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
Figure 75. Variation de vitesse des
générateurs du 1er cas,
a :
2ème scénario, b :
3ème scénario.
Les informations obtenues concernant le dépassement
maximum et le temps de réponse du système pour les deux
scénarios sont données dans le tableau suivant.
|
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
2ème
scénario
|
Dp
|
5.65×10-3
|
10.6×10-3
|
4.42×10-3
|
- 9.28×10-3
|
1.34×10-3
|
|
tr (s)
|
8
|
7
|
8
|
10
|
9
|
|
3ème
scénario
|
Dp
|
4.7×10-3
|
10.6×10-3
|
4.6×10-3
|
- 10.1×10-3
|
- 2.26×10-3
|
|
tr (s)
|
14
|
11
|
14
|
10
|
9
|
Nous remarquons sur ce tableau que certaines valeurs du
dépassement maximum sont plus importantes que pour le premier
scénario tandis que d'autres sont plus faibles. Par contre, les temps de
réponse des deuxième et troisième scénarios sont
toujours supérieurs ou égaux à ceux du premier
scénario ; les temps de réponse des générateurs 53
et 60 du troisième scénario sont doublés (ils
dépassent même les 10 secondes).
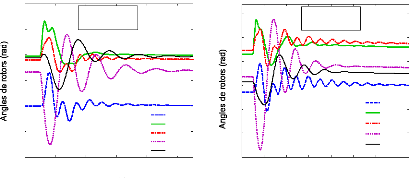
Enfin, pour compléter cette étude, nous donnons la
réponse dynamique des angles de rotor suite au défaut de ligne
pour les 2ème et 3ème scénarios,
figure (76).
4.5.3.5- Conclusion.
Dans l'étude du premier cas, nous avons utilisé
la méthode des facteurs de participation pour localiser les PSSs
nécessaires au système et la méthode des AGs pour
régler les paramètres de ces PSSs. Les résultats
trouvés pour le point de fonctionnement nominal montrent que le
réglage du système est efficace avec un bon amortissement pour
tous les modes. La performance du réglage a été
évaluée avec les modèles linéaire et
non-linéaire du système. Par ailleurs, nous trouvons que la
performance s'est dégradée pour les autres
scénarios, en particulier pour le troisième
scénario ; les critères liés à la zone de
stabilité et au temps de réponse étant "mal
respectés" pour plusieurs modes (notamment les interrégionaux).
La robustesse du réglage n'est donc pas suffisamment assurée.
Nous pouvons donc conclure que, bien que le programme d'AG
utilisé tienne compte des interactions entre les PSSs et réalise
un réglage coordonné en comblant ainsi les limites des
méthodes classiques, il reste à son tour handicapé par la
prédétermination des lieux d'installation des PSSs. Cela nous
amène à utiliser aussi l'AG dans le choix optimal de localisation
des PSSs.
2.5
2
1er cas,
2ème scénario
2
1er cas,
3ème scénario
1.5
1.5
1
1
0.5
0.5
0
-0.5 0 2 4 6 8 10
Temps (s)
G. 53
G. 59
G. 60
G. 66
G. 68
-1 0 2 4 6 8 10 12 14
Temps (s)
0
-0.5
G. 53
G. 59
G. 60
G. 66
G. 68
a b
Figure 76. Réponse dynamique des
angles de rotor du 1er cas,
a :
2ème scénario, b :
3ème scénario.
4.5.4- Cas 2 : optimisation des paramètres et de
la localisation des PSSs. 4.5.4.1- Application des AGs.
Les méthodes de détermination classique de
l'emplacement des PSSs, tels les facteurs de participation, peuvent ne pas
garantir une performance efficace en termes d'amortissement d'oscillation, en
particulier, pour les modes interrégionaux où un grand nombre de
générateurs est souvent impliqué. En outre, ces
méthodes ne prennent pas en considération les éventuelles
interactions indésirables des PSSs.
Dans ce cas, nous allons considérer les lieux
d'emplacement, comme les paramètres de réglage des PSSs, comme
des variables à optimiser. Le nombre de PSSs à installer reste
constant et égal à celui déterminé par la
méthode des facteurs de participation, soit 14 PSSs.
Pour ce faire, nous appliquons la même fonction
multiobjectif donnée par la relation (141) et nous développons un
AG permettant d'introduire la localisation d'un PSS comme un paramètre
optimisable. Nous appliquons donc une optimisation simultanée de
localisation et des paramètres des PSSs.
La figure (77) donne une représentation graphique de cette
procédure d'optimisation cordonnée.
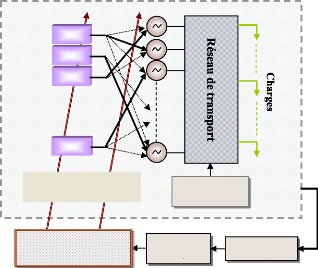
Algorithme Génétique
Paramètres
des PSSs
PSS 14
PSS 1
PSS 2
PSS 3
Placement
des PSSs
Fonction
multiobjectif
G16
G2
G3
G1
Point de
fonctionnement
Valeurs propres
Figure 77. Optimisation coordonnée de
localisation et des paramètres des PSSs.
Les quatre variables à optimiser pour chaque PSS
(l'emplacement, un gain et deux constantes de temps) sont soumises aux
contraintes suivantes :
0.1 45
= =
K PSS j
,
0 .00 1 0 . 1
= =
T 1 , j
0 .00 1 0 . 1
= =
T 3 , j
(148)
|
PLPSS
|
,
|
j
|
{ }
53, ,6 8
L
|
|
avec
|
j
|
1,2,
|
|
, NPSS
|
Les autres paramètres (Tw,j
et T2,j, T4,j) des PSSs sont considérés
constants : Tw,j = 10 et T2,j = T4,j = 0.02.
Le tableau (11) donne les valeurs choisies des paramètres
de l'AG.
|
Nombre d'individu Nind
|
100
|
|
Nombre de gènes Ngens
|
Nind x Nvar
|
|
Nombre de génération Ngener
|
300
|
|
Probabilité de croisement Pc
|
0.9
|
|
Probabilité de mutation Pm
|
0.005
|
Tableau 11. Valeurs choisies des
paramètres de l 'AG.
L'évolution de la fonction multiobjectif en fonction du
nombre de générations, donnée à la figure (78),
montre que sa valeur finale optimale est égale à 1.552.
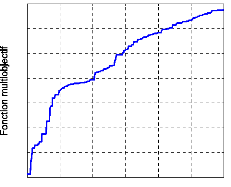
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2 0 50 100 150 200 250 300
Générations
Figure 78. Evolution de la fonction
multiobjectif.
Les résultats, donnés au tableau (12),
représentent les valeurs optimales de l'emplacement des PSSs et leurs
paramètres de réglage.
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
53
|
3 1.3445
|
0.0980
|
0.0985
|
|
2
|
54
|
44.3561
|
0.0881
|
0.0770
|
|
3
|
55
|
44.2500
|
0.08 12
|
0.0466
|
|
4
|
57
|
24.5247
|
0.0609
|
0.0784
|
|
5
|
58
|
07.8640
|
0.0398
|
0.0478
|
|
6
|
59
|
24.7385
|
0.0567
|
0.0654
|
|
7
|
61
|
16.0132
|
0.0729
|
0.0366
|
|
8
|
62
|
08.6426
|
0.0533
|
0.0742
|
|
9
|
63
|
04.8510
|
0.0632
|
0.0787
|
|
10
|
64
|
17.0964
|
0.0924
|
0.0237
|
|
11
|
65
|
43.8049
|
0.0026
|
0.0115
|
|
12
|
66
|
44.4671
|
0.0108
|
0.0034
|
|
13
|
67
|
44.7417
|
0.0204
|
0.0159
|
|
14
|
68
|
44.4898
|
0.0102
|
0.0054
|
Tableau 12. Paramètres et
localisation des PSSs optimisés par AG.
Nous allons dans la suite de ce paragraphe analyser la
performance et la robustesse du réglage des PSSs lors de la
linéarisation du modèle du système et lors de
l'utilisation du modèle non-linéaire.
4.5.4.2- Analyse des valeurs propres. 4.5.4.2.1- Le
point de fonctionnement nominal.
Pour calculer les valeurs propres du système au point
de fonctionnement nominal en boucle fermée, nous installons les 14 PSSs
optimisés aux emplacements déterminés par l'AG. Le tableau
(13) donne les valeurs propres dominantes ; leur répartition dans le
plan complexe est donnée à la figure (79).
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 6.7752 #177; j 11.413
|
0.5104
|
1.8166
|
|
2
|
- 2.2305 #177; j 10.556
|
0.2067
|
1.6801
|
|
3
|
- 6.9634 #177; j 8.6133
|
0.6287
|
1.3709
|
|
4
|
- 1.4778 #177; j 8.3524
|
0.1742
|
1.3293
|
|
5
|
- 2.7045 #177; j 8.2624
|
0.3111
|
1.3150
|
|
6
|
-1.6588 #177; j 7.4513
|
0.2173
|
1.1859
|
|
7
|
- 1.3803 #177; j 7.3761
|
0.1839
|
1.1739
|
|
8
|
- 1.3779 #177; j 7.2170
|
0.1875
|
1.1486
|
|
9
|
- 4.8218 #177; j 2.7800
|
0.8663
|
0.4425
|
|
10
|
- 2.0778 #177; j 2.6504
|
0.6170
|
0.4218
|
|
11
|
- 3.6124 #177; j 2.3486
|
0.8384
|
0.3738
|
|
12
|
- 1.3974 #177; j 3.9670
|
0.3322
|
0.6314
|
|
13
|
- 1.3777 #177; j 3.9719
|
0.3277
|
0.6321
|
|
14
|
- 2.7954 #177; j 6.1612
|
0.4132
|
0.9806
|
|
15
|
- 1.5958 #177; j 2.0264
|
0.6187
|
0.3225
|
Tableau 13. Valeurs propres du
système (14 PSSs localisés et optimisés par AG).
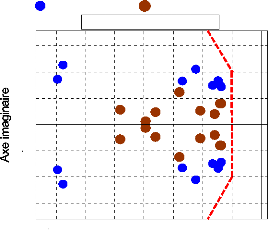
2ème cas , 1er scénario
dz = 10 %
5
0
-5
-10
-15
-7 -6 -5 -4 -3 -2 -1 0
-1
Modes locaux Modes interrégionaux
15
10
Axe réel
Figure 79. Répartition des valeurs
propres du système dans le plan complexe
(14 PSSs localisés et
optimisés par A G).
L'examen de ces valeurs propres montre que le facteur
d'amortissement minimum est æmin = 17.42 % et que la partie
réelle maximale des valeurs propres est ómax = - 1.3777.
Nous remarquons aussi que tous les modes, locaux et interrégionaux, sont
bien déplacés dans la zone D. Le facteur d'amortissement
et la partie réelle des valeurs propres des modes interrégionaux
sont notamment améliorés par rapport au premier cas. Nous
constatons donc une bonne amélioration de la stabilité globale du
système. Cette amélioration se traduit par des
améliorations sur le facteur d'amortissement minimum (de 16.1 % en
valeur relative) et sur la partie réelle maximale des valeurs propres
(de 45.18 % en valeur relative) par rapport au premier cas.
Pour s'assurer de cette amélioration dans tous les
scénarios probables, nous devons examiner, comme nous avons fait pour le
premier cas, les deux autres scénarios proposés.
4.5.4.2.2- Les autres
scénarios.
Les répartitions des valeurs propres dans le plan complexe
des deuxième et troisième scénarios sont données
respectivement à la figure (80).
Modes locaux Modes interrégionaux


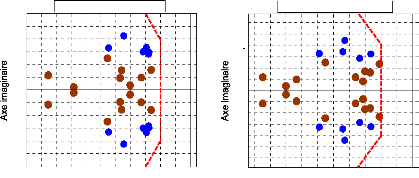
15
15
dz = 10 %
dz = 10 %
10
10
5
5
0
0
-5
-5
-10
-10
-15
-15
-5 -4 -3 -2 -1 0
-1
-5 -4 -3 -2 - 0
-1
2ème cas , 2ème scénario
2ème cas , 3ème scénario
Axe réel Axe réel
a b
Figure 80. Valeurs propres du
système pour le 2ème cas,
a :
2ème scénario, b :
3ème scénarios.
Les valeurs minimales de (æ) et maximales de
(ó) des deux scénarios sont données
respectivement comme suit :
|
æmin
|
ómax
|
|
Scénario 2
|
17.53 %
|
- 1.3076
|
|
Scénario 3
|
16.20 %
|
-1.0437
|
Sur ces deux figures, il est clair que tous les modes (locaux
et interrégionaux) associés aux deux scénarios se trouvent
placés dans la zone D ; les valeurs critiques de
(æi) et (ói) sont bien respectées avec
une marge très importante pour le facteur d'amortissement. Ces
valeurs
présentent une bonne amélioration des
performances par rapport au premier cas. Cela se traduit par une augmentation
de (æmin) de (65.8 % et 151.16 %) et une diminution
de (ómax) de (108.1 % et 178.8 %) pour les deux
scénarios respectivement.
Cette comparaison peut être illustrée graphiquement,
par rapport au premier scénario, par la figure suivante.
a b
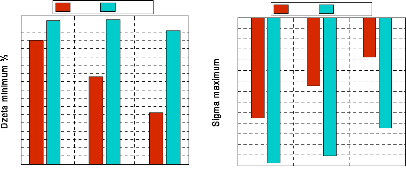
18
16
14
12
10
4
8
6
2
0
1er scénario 2ème scénario 3ème
scénario
1er cas 2ème cas
-0.2
-0.4
-0.6
-0.8
-1.2
-1.4
-1
0
1er scénario 2ème scénario 3ème
scénario
1er cas 2ème cas
Figure 81. Comparaison entre le
1er et le 2ème cas.
a : æmin, b
: ómax.
D'après cette figure, nous constatons que le
réglage du deuxième cas respecte les critères de la zone
D de stabilité pour les trois scénarios étudies
contrairement au premier cas qui ne la respectait que par le scénario du
point de fonctionnement nominal.
4.5.4.3- Analyse par simulations temporelles.
4.5.4.3.1- Le point de fonctionnement nominal.
Nous examinons dans ce paragraphe les simulations temporelles du
système non-linéaire au point de fonctionnement nominal pour le
même défaut appliqué au premier cas.
Le résultat de la variation de vitesse des cinq
générateurs est présenté à la figure
(82).
Pour mieux comparer ce résultat à son homologue
du premier cas, nous donnons dans les tableaux suivants le dépassement
maximum et le temps de réponse mesurés sur ces courbes, en
rappelant aussi ceux du premier cas.
|
2ème
cas
|
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
Dp
|
5.42×10-3
|
10.7×10-3
|
5.01×10-3
|
- 9.85×10-3
|
0.49×10-3
|
|
tr (s)
|
5
|
5
|
8
|
4
|
4
|
|
1er
cas
|
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
Dp
|
5.48×10-3
|
10.6×10-3
|
5.01×10-3
|
- 9.84×10-3
|
0.49×10-3
|
|
tr (s)
|
7
|
7
|
8
|
8
|
8
|
Nous constatons que les temps de réponse sont notamment
améliorés ; les oscillations de générateurs 66 et
68 par exemple s'amortissent deux fois plus rapidement que leurs
équivalentes au premier cas, les valeurs des dépassements restant
les mêmes.
Cette amélioration obtenue par le modèle
non-linéaire est en bon accord avec celle obtenue par le modèle
linéaire.
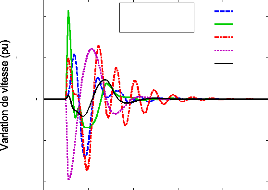
-0.005
0.005
-0.01
0.01
0
2ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0 2 4 6 8 10
Temps (s)
Figure 82. Variations de vitesse des cinq
générateurs suite à un défaut de ligne,
(1er
scénario du 2ème cas).
Les réponses temporelles des angles de rotor et les
écarts entre les angles des générateurs 60 et 66 et entre
les angles des générateurs 68 et 53, donnés à la
figure (83), montrent bien la restauration rapide de la stabilité suite
au défaut et le bon amortissement obtenu.
Temps (s) Temps (s)
a b
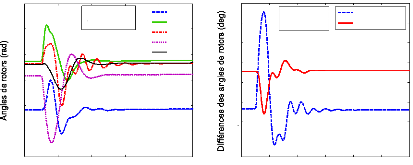
120
100
80
60
40
20
0
-20
0 2 4 6 8 10 12
-0.5 0 2 4 6 8 10
2.5
0.5
1.5
2
0
1
2ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
2ème cas,
1er scénario
(G. 60 - G. 66)
(G. 68 - G. 53)
Figure 83. Réponse dynamique des
générateurs (1er scénario du
2ème cas),
a : angles de rotor,
b : écart des angles de deux paires.
La réponse dynamique des puissances électriques des
cinq générateurs choisis et la réponse dynamique des
tensions de quelques noeuds sont présentées à la figure
(84).
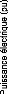
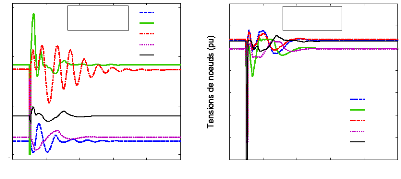
0.5
1.5
0
1
0 2 4 6 8 10
2ème cas,
1er scénario
Temps (s)
G. 53
G. 59
G. 60
G. 63
G. 66
0.8
0.6
0.4
0.2
1.4
1.2
0 0 2 4 6 8 10
Temps (s)
1
2ème cas,
1er scénario
Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59
a b
Figure 84. Réponse dynamique du
système (1er scénario du 2ème
cas),
a : puissances électriques, b
: tensions des noeuds.
4.5.4.3.2- Les autres
scénarios.
Pour analyser la performance de régulation du
système lors de la restauration de la stabilité suite à un
défaut sévère, nous montrons tout d'abord la variation de
vitesse des cinq générateurs pour les deux scénarios,
figure (85).
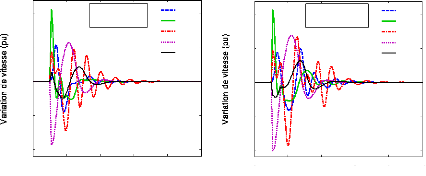
0.005
0.01
2ème cas,
2ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0.005
0.01
2ème cas,
3ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0
0
-0.005
-0.005
-0.01
0 2 4 6 8 10
Temps (s)
-0.01
0 2 4 6 8 10
Temps (s)
a b
Figure 85. Variation de vitesse des
générateurs du 2ème cas,
a
: 2ème scénario, b :
3ème scénario.
Nous donnons ensuite dans le tableau suivant le
dépassement maximum et le temps de réponse mesurés pour la
variation de vitesse.
|
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
2ème
scénario
|
Dp
|
5.45×10-3
|
10.6×10-3
|
4.43×10-3
|
- 9.29×10-3
|
1.35×10-3
|
|
tr (s)
|
5
|
4
|
7
|
4
|
4
|
|
3ème
scénario
|
Dp
|
4.39×10-3
|
10.6×10-3
|
4.6×10-3
|
- 10.2×10-3
|
- 2.2×10-3
|
|
tr (s)
|
7
|
6
|
8
|
4
|
5
|
Nous comparons enfin les temps de réponse avec leurs
équivalents du premier cas, en tenant compte des trois scénarios
retenus. Nous représentons cette comparaison par la figure (86). La
figure (87), quant à elle, représente l'amélioration
apportée par l'utilisation de l'AG pour l'optimisation simultanée
des paramètres des PSSs et de leurs emplacements. L'amélioration
de temps de réponse a été évaluée, en
valeurs relatives exprimées en pourcent pour les cinq
générateurs choisis et dans les trois scénarios
étudiés.
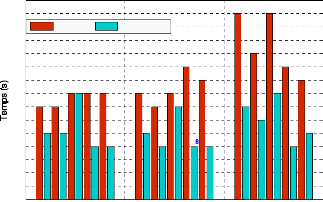
14
12
10
4
6
2
8
0
53
53
59
1er cas 2ème cas
59
606066
66
68
68
53
53
59
59
60
60
66
6
68
68
53
53
59
59
60
60
66
66
68
68
1er Scénario 2ème Scénario 3ème
Scénario
Figure 86. Temps de réponse des
trois scénarios (comparaison entre le 1er et le
2ème cas).
60%
50%
40%
30%
20%
10%
0%

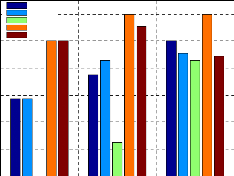
G. 53
G. 59
G. 60
G. 66
G. 68
1er Scénario 2ème Scénario 3ème
Scénario
Figure 87. Temps de réponse des
trois scénarios
(Comparaison des valeurs relatives entre le
1er et le 2ème cas).
Nous remarquons que le deuxième cas présente une
amélioration remarquable des temps de réponse quel que soit le
scénario ; cette amélioration atteint par exemple 60 % pour la
variation de vitesse de générateur 66 avec les deuxième et
troisième scénarios.
La figure (88) montre enfin la réponse dynamique des
angles de rotor suite au défaut de ligne pour les 2ème
et 3ème scénarios.
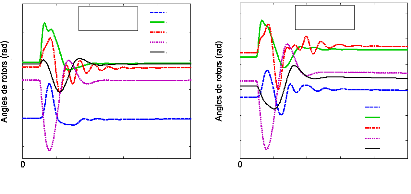
2 4 6 8 10
Temps (s)
2 4 6 8 10
Temps (s)
2.5
2
2ème cas,
2ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
1.5
2
2ème cas,
3ème scénario
1.5
1
1
0.5
0.5
0
-0.5
0
G. 53
G. 59
G. 60
G. 66
G. 68
a b
Figure 88. Réponse dynamique des
angles de rotor du 2ème cas,
a :
2ème scénario, b :
3ème scénario.
4.5.4.4- Discussion et conclusion.
La méthode des facteurs de participation a
montré que les générateurs 53 et 66 ne devraient pas
être équipés de PSSs. Pourtant, selon cette méthode,
le générateur 66 participe aux modes interrégionaux ; le
générateur 53 quant à lui ne présente aucune
participation importante aux modes du système.
Lorsque l'AG est utilisé pour trouver les
générateurs les plus appropriés pour installer des PSSs,
il prend en considération l'ensemble des propriétés des
PSSs (emplacement et paramètres). Il varie continuellement l'emplacement
et les valeurs de paramètres des PSSs en cherchant à trouver la
solution qui améliore au maximum la performance de tous les modes.
Lorsque l'AG trouve qu'un emplacement n'entraîne aucune
amélioration de la performance des modes ou a éventuellement une
influence négative, l'emplacement est abandonné.
L'AG a montré que tous les générateurs
responsables des modes interrégionaux (comme la méthode des
facteurs de participation a déterminé) nécessitent l'ajout
de PSSs, en particulier le générateur 66. Par contre, pour ceux
responsables des modes locaux, l'AG montre que deux d'entre eux n'ont pas
besoin de PSSs ; à savoir les générateurs 56 et 60.
La figure (89) montre la fréquence de sélection de
chaque générateur pour être doté d'un PSS pour 300
d'itérations d'AG.
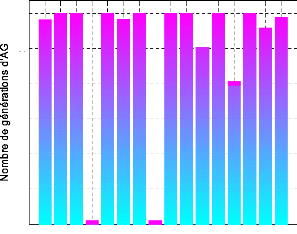
0
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
300
250
200
150
100
50
Numéro de générateur
Figure 89. Choix de chaque
générateur pour 300 d'itérations d'AG.
Il apparaît sur cette figure que les
générateurs 56 et 60 ne sont choisis que pendant quelques
itérations d'AG. Les générateurs 63 et 65 sont moins
choisis par rapport aux autres. La question qui se pose maintenant est la
suivante : l'AG peut-il être employé pour réduire le nombre
de PSSs en conservant seulement les PSSs les plus efficaces ???
4.5.5- Cas 3 : optimisation globale des PSSs. 4.5.5.1-
Application des AGs.
Généralement, lorsque les PSSs sont mal
réglés, ils peuvent produire des effets sévèrement
nuisibles au système de puissance. En outre, un ensemble de PSSs peut
donner des résultats médiocres quand son emplacement n'est pas
bien choisi. En conséquence, il est nécessaire de réduire
ces effets nuisibles en choisissant l'emplacement optimal des PSSs
simultanément avec un réglage coordonné et en employant
seulement le nombre nécessaire de PSSs.
Pour la réduction du nombre des PSSs, nous proposons la
procédure illustrée par la figure (90). Cette figure montre la
structure du programme de l'AG utilisé. Un commutateur branché en
série avec le PSS prend des variables "0 ou 1". Les variables
représentant ces commutateurs sont introduites dans le programme de l'AG
avec les autres variables des PSSs (ceux du deuxième cas). Ces
commutateurs permettent de relier (si la variable est 1) ou débrancher
(si la variable est 0) les PSSs des générateurs. Au cours du
calcul, lorsque la fonction multiobjectif ne varie pas de manière
significative à cause de la faible influence de certains PSS sur
l'amortissement du système, l'AG ne les prend pas alors en
considération.
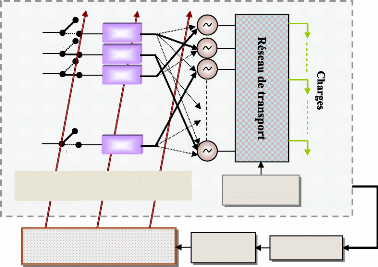
Interrupteurs
des PSSs
Algorithme Génétique
00
01
1
1
0
1
Paramètres
des PSSs
PSS 16
PSS 1
PSS 2
PSS 3
Placement
des PSSs
Fonction
multiobjectif
G16
G2
G3
G1
Point de
fonctionnement
Valeurs propres
Figure 90. Optimisation coordonnée de
localisation, des paramètres et du nombre des PSSs.
Les cinq variables à optimiser de chaque PSS (un
commutateur de PSS, un emplacement, un gain et deux constantes de temps) sont
soumises aux contraintes suivantes :
1 40
= =
K PSS j
,
0. 0 1 0 . 1
= =
T 1 , j
0. 0 1 0 . 1
= =
T 3 , j
{ }
5 3, ,6 8
L
{ }
0,1
PLPSS , j SWPSS ,j
(149)
j

1,2,
avec
, NPSS
Les autres paramètres (Tw,j
et T2,j, T4,j) des PSSs sont considérés
constants : Tw,j = 10 et T2,j = T4,j = 0.02.
Le tableau (14) donne les valeurs choisies des paramètres
de l'AG.
|
Nombre d'individu Nind
|
100
|
|
Nombre de gènes Ngens
|
Nind x Nvar
|
|
Nombre de génération Ngener
|
300
|
|
Probabilité de croisement Pc
|
0.7
|
|
Probabilité de mutation Pm
|
0.005
|
Tableau 14. Valeurs choisies des
paramètres de l'AG.
Nous avons trouvé que les meilleures performances des
paramètres obtenus par l'AG demandent l'utilisation de 12 PSSs
seulement.
Les valeurs des paramètres des PSSs optimisés sont
données dans le tableau (15).
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
53
|
21.5146
|
0.0926
|
0.0998
|
|
2
|
54
|
38.1806
|
0.0874
|
0.0225
|
|
3
|
55
|
39.1358
|
0.0978
|
0.0560
|
|
4
|
57
|
20.4600
|
0.0887
|
0.0562
|
|
5
|
58
|
23.9224
|
0.0639
|
0.0452
|
|
6
|
59
|
11.6205
|
0.0754
|
0.0160
|
|
7
|
61
|
39.2348
|
0.0297
|
0.0948
|
|
8
|
62
|
21.8183
|
0.0324
|
0.0411
|
|
9
|
64
|
18.8449
|
0.0423
|
0.0480
|
|
10
|
66
|
39.7833
|
0.0138
|
0.0174
|
|
11
|
67
|
39.2614
|
0.0147
|
0.0100
|
|
12
|
68
|
39.9553
|
0.0512
|
0.0395
|
Tableau 15. Paramètres et
localisation des PSSs optimisés par AG.
Ces valeurs représentent la meilleure solution atteinte
à la dernière génération ; elles correspondent
à la valeur finale de la fonction multiobjectif, soit 1.223.
L'évolution de la fonction multiobjectif en fonction du nombre de
générations est donnée à la figure (91).
0 50 100 150 200 250 300
Générations
Figure 91, Evolution de la fonction
multiobjectif.
Cette évolution de la fonction multiobjectif correspond
à l'évolution du nombre de PSSs au cours de l'exécution de
l'AG ; cette dernière évolution est illustrée par la
figure (92).
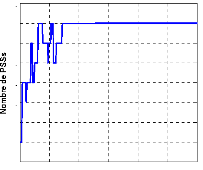
13
12
11
10
9
8
7
6
5
0 50 100 150 200 250 300
Nombre de génération
Figure 92. Convergence du nombre de
PSSs.
Comme nous avons fait avec les cas précédents,
nous devons analyser la performance et la robustesse du réglage des PSSs
pour le modèle linéaire du système et aussi pour son
modèle non-linéaire.
4.5.5.2- Analyse des valeurs propres. 4.5.5.2.1- Le
point de fonctionnement nominal.
En installant les 12 PSSs optimisés aux emplacements
déterminés par l'AG, nous pouvons calculer les valeurs propres du
système au point de fonctionnement nominal en boucle fermée. Le
tableau (16) donne certaines de ces valeurs propres. La figure (93) donne leurs
répartitions dans le plan complexe.
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 7.9207 #177; j 9.7480
|
0.6306
|
1.5514
|
|
2
|
- 2.1271 #177; j 10.888
|
0.1917
|
1.7329
|
|
3
|
- 1.4055 #177; j 9.8537
|
0.1412
|
1.5683
|
|
4
|
- 1.3155 #177; j 9.3297
|
0.1396
|
1.4849
|
|
5
|
- 1.6215 #177; j 8.4449
|
0.1886
|
1.3440
|
|
6
|
- 1.0859 #177; j 7.2412
|
0.1483
|
1.1525
|
|
7
|
- 1.8724 #177; j 7.0410
|
0.2570
|
1.1206
|
|
8
|
- 4.4445 #177; j 3.8309
|
0.7575
|
0.6097
|
|
9
|
- 7.2122 #177; j 4.7003
|
0.8378
|
0.7481
|
|
10
|
- 3.9322 #177; j 2.7953
|
0.8150
|
0.4449
|
|
11
|
- 2.6229 #177; j 3.0356
|
0.6538
|
0.4831
|
|
12
|
- 1.0934 #177; j 3.9569
|
0.2663
|
0.6298
|
|
13
|
- 1.0836 #177; j 2.7449
|
0.3672
|
0.4369
|
|
14
|
- 1.0862 #177; j 3.0984
|
0.3308
|
0.4931
|
|
15
|
- 1.6932 #177; j 3.3940
|
0.4464
|
0.5402
|
Tableau 16. Valeurs propres du
système (12 PSSs : optimisation globale par AG).
Modes locaux Modes interrégionaux


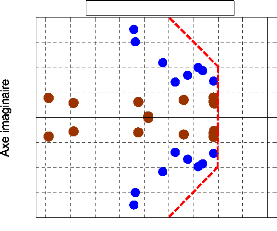
3ème cas , 1er scénario
20
dz = 10 %
10
0
-10
-4 -3 -2 -1 0
-1
-20
Axe réel
Figure 93. Répartition des valeurs
propres du système dans le plan complexe
(12 PSSs : optimisation
globale par AG).
L'installation de ces 12 PSSs dans le système permet
d'assurer la stabilité globale du système ; tous les modes,
locaux et interrégionaux, sont bien décalés dans la zone
D. Le facteur d'amortissement minimum est æmin = 13.96
% et la partie réelle maximale des valeurs propres est
ómax = - 1.0836. En comparant avec le premier cas, nous
remarquons que nous obtenons quasiment la même performance avec 12 PSSs
seulement qu'avec 14 PSSs. (Le facteur d'amortissement minimum est
diminué de 7 % tandis que la partie réelle maximale des valeurs
propres est améliorée de 14.2 %). En outre, le facteur
d'amortissement et la partie réelle des valeurs propres des modes
interrégionaux présentent une bonne amélioration par
rapport au premier cas.
4.5.5.2.2- Les autres
scénarios.
Nous avons vu que les 12 PSSs optimisés et
localisés par l'AG placent tous les modes du système dans la zone
D en cas de point de fonctionnement nominal. Quant aux deux autres
scénarios proposés, les répartitions des valeurs propres
associées dans le plan complexe sont données à la figure
(94).
Nous trouvons sur ces deux figures qu'il n'y a qu'un seul mode
hors de la zone D pour le deuxième scénario et deux
modes pour le troisième scénario. Pour l'un comme pour l'autre,
le critère de la partie réelle des valeurs propres n'est pas
respecté tandis que le critère du facteur d'amortissement reste
toujours respecté. Les caractéristiques générales
de ces modes critiques peuvent être données dans le tableau
suivant :
|
N° mode
|
ë
|
æ
|
f [Hz]
|
Type de mode
|
|
2ème
scénario
|
1
|
- 0.4202#177; j 2.9600
|
0.1543
|
0.4281
|
Interrégional
|
|
3ème
scénario
|
1
|
- 0.8968#177; j 6.6542
|
0.1336
|
1.0586
|
Local
|
|
2
|
0.9237#177; j 3.2530
|
0.2732
|
0.5177
|
Interrégional
|
Ce tableau montre que le seul mode critique du
2ème scénario est interrégional tandis qu'un
mode local et un autre interrégional sont associés au
3ème scénario.
Modes locaux Modes interrégionaux


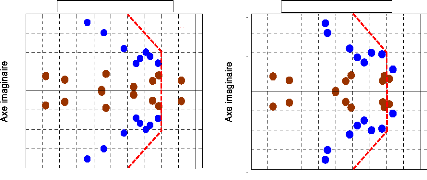
3ème cas , 3ème scénario
dz = 10 %
-4 -3 -2 -1 0
-1
3ème cas , 2ème scénario
20
dz = 10 %
10
0
-10
-4 -3 -2 -1 0
-1
-20
20
10
0
-10
-20
Axe réel Axe réel
a b
Figure 94. Valeurs propres du
système pour le 3ème cas,
a :
2ème scénario, b :
3ème scénarios.
Les valeurs minimales de (æ) et maximales de
(ó) des deux scénarios sont données ci- dessous
:
|
æmin
|
ómax
|
|
Scénario 2
|
14.51 %
|
- 0.4202
|
|
Scénario 3
|
11.77 %
|
- 0.8968
|
Nous comparons les variations relatives des valeurs critiques
de (æi) et (ói) de chaque scénario de ce
cas par rapport au premier cas. Cette comparaison est donnée dans le
tableau (17) et illustrée par la figure (95).
|
Äæmin %
|
Äómax %
|
|
Scénario 1
|
- 7 %
|
14.2 %
|
|
Scénario 2
|
37.27 %
|
- 33.13 %
|
|
Scénario 3
|
82.48 %
|
118.22 %
|
Tableau 17. Comparaison des variations
relatives de (æmin) et (ómax)
entre les 1er et 3ème cas.
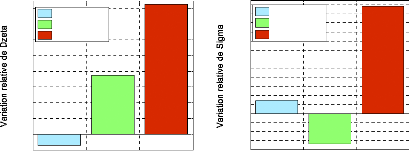
-10 %
40 %
20 %
80 %
60 %
0 %
1er scénario 2ème scénario 3ème
scénario
120 %
100 %
-20 %
-40 %
40 %
80 %
60 %
20 %
0 %
1er scénario 2ème scénario 3ème
scénario
a b
Figure 95. Comparaison des variations
relatives entre les 1er et 3ème cas,
a
: æmin, b : ómax.
Nous constatons donc qu'il y a une amélioration globale
sur la performance de régulation lors de l'utilisation de 12 PSSs
optimisés et localisés simultanément par l'AG par rapport
au premier cas utilisant 14 PSSs localisés par une méthode
classique et optimisés par l'AG.
4.5.5.3- Analyse par simulations temporelles.
4.5.5.3.1- Le point de fonctionnement nominal.
Pour continuer la vérification de la performance de
réglage, nous devons réaliser des simulations temporelles
adaptées du système non-linéaire. Nous considérons
dans ce paragraphe le système avec son point de fonctionnement nominal
soumis au défaut appliqué aux cas précédents.
Nous donnons en premier lieu le résultat de la variation
de vitesse des cinq générateurs ; il est présenté
à la figure (96).
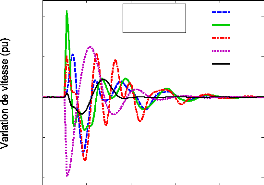
0.005
0.01
3ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0
-0.005
-0.01
0 2 4 6 8 10
Temps (s)
Figure 96. Variations de vitesse des cinq
générateurs suite à un défaut de
ligne,
(1er scénario du 3ème
cas).
Les valeurs des dépassements maximums et des temps de
réponse sont données dans le tableau suivant.
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
Dp
|
5.29×10-3
|
10.7×10-3
|
5.01×10-3
|
- 9.84×10-3
|
0.49×10-3
|
|
tr (s)
|
8
|
8
|
8
|
6
|
3
|
En comparant les valeurs de ce tableau avec les valeurs
équivalentes du premier cas, nous constatons que les temps de
réponse des générateurs 66 et 68 ont bien diminués
tandis que ceux des générateurs 53 et 59 ont
légèrement augmentés (de 1 seconde). Les
dépassements conservent les mêmes valeurs.
La figure (97) montre les réponses temporelles des
angles de rotor pour le défaut proposé et les écarts entre
les angles des générateurs 60 et 66 et entre les angles des
générateurs 68 et 53. Les oscillations interrégionales se
manifestent clairement sur l'écart angulaire des
générateurs appartenant à des régions
différentes. Nous pouvons bien voir que ces oscillations
interrégionales s'amortissent en respectant le critère de
performance désirée.
Temps (s) Temps (s)
a b
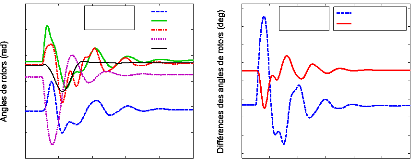
-0.5 0 2 4 6 8 10
2.5
0.5
1.5
2
0
1
3ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
120
100
-20
-40
40
80
60
20
0
0 2 4 6 8 10 12
3ème cas,
1er scénario
(G. 60 - G. 66)
(G. 68 - G. 53)
Figure 97. Réponse dynamique des
générateurs (1er scénario du
3ème cas),
a : angles de rotor,
b : écart des angles de deux paires.
La réponse dynamique des puissances électriques des
cinq générateurs choisis et la réponse dynamique des
tensions de quelques noeuds sont illustrées par la figure (98).
Ces simulations dynamiques montrent clairement que
malgré le nombre réduit des PSSs, l'optimisation globale par l'AG
permet au système de retrouver sa stabilité après quelques
secondes.
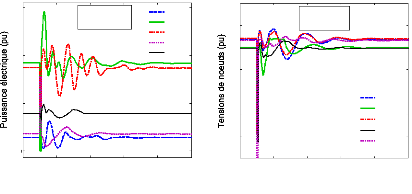
1.5
1
3ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 63
G. 66
1.4
1.2
1
3ème cas,
1er scénario
0.8
0.5
0.6
0.4
0.2
Nd. 40 Nd. 42 Nd. 48 Nd. 52 Nd. 59
0
0 2 4 6 8 10
Temps (s)
0 0 2 4 6 8 10
Temps (s)
a b
Figure 98. Réponse dynamique du
système (1er scénario du 3ème
cas),
a : puissances électriques, b
: tensions des noeuds.
4.5.5.3.2- Les autres
scénarios.
Nous donnons aux figures (99) et (100) respectivement, la
réponse dynamique de la variation de vitesse des cinq
générateurs et la réponse dynamique des angles de rotor
pour les deux scénarios proposés.
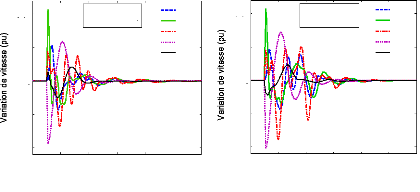
0.005
0.01
3ème cas,
2ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0.005
0.01
3ème cas,
3ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0
0
-0.005
-0.005
-0.01
0 2 4 6 8 10 12
Temps (s)
-0.01
0 2 4 6 8 10 12
Temps (s)
a b
Figure 99. Variation de vitesse des
générateurs du 3ème cas,
a
: 2ème scénario, b :
3ème scénario.
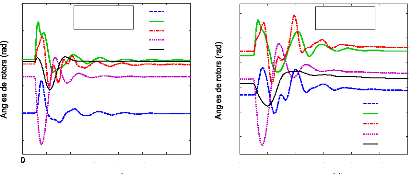
2 4 6 8 10 12 14
Temps (s)
0 2 4 6 8 10 12
Temps (s)
2.5
2
3ème cas,
2ème scénario
G. 53
G. 59
G. 60
G. 66
G. 68
1.5
2
3ème cas,
3ème scénario
1.5
1
1
0.5
0.5
0
-0.5
0
G. 53
G. 59
G. 60
G. 66
G. 68
a b
Figure 100. Réponse dynamique des
angles de rotor du 3ème cas,
a :
2ème scénario, b :
3ème scénario.
Suite au défaut proposé et comme nous l'avons
fait pour les cas précédents, nous caractérisons la
réponse dynamique du système par le calcul du dépassement
maximum et du temps de réponse des générateurs. Les
valeurs obtenues pour les deux scénarios sont données dans le
tableau suivant.
|
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
2ème
scénario
|
Dp
|
5.39×10-3
|
10.7×10-3
|
4.43×10-3
|
- 9.28×10-3
|
1.34×10-3
|
|
tr (s)
|
9
|
9
|
10
|
7
|
4
|
|
3ème
scénario
|
Dp
|
4.6×10-3
|
10.7×10-3
|
4.6×10-3
|
- 10.2×10-3
|
- 2.19×10-3
|
|
tr (s)
|
8
|
8
|
9
|
7
|
6
|
Nous remarquons sur ce tableau qu'il y a
généralement une amélioration du temps de réponse
à scénarios équivalents par rapport au 1er cas. En outre,
il n'y a plus de temps de réponse dépassant les 10 secondes.
4.5.5.4- Evaluation du nombre de modes dans les trois
cas.
Dans la mise en oeuvre conventionnelle des PSSs, les
méthodes classiques d'emplacement (tels les facteurs de participation,
...) ne prennent pas en compte du changement de la participation des
générateurs dans l'évolution des modes en présence
des PSSs et des interactions indésirables entre ces PSSs. Par
conséquent, nous trouvons que la plupart des modes
électromécaniques dans les trois scénarios
étudiés (au 1er cas) sont de nature
interrégionale (70 % en moyenne, figure (101, a)).
Par contre l'optimisation simultanée des
paramètres et de l'emplacement des PSSs permet une diminution importante
du nombre des modes interrégionaux associés (40 % des modes
interrégionaux pour le 2ème cas et 55 % dans le
3ème cas, figure (101, b et c)).

Modes locaux
Modes interrégionaux
70 %
a
30 %
40 %
55 %
60 %
45 %
b c
Figure 101. Taux % des modes locaux et
interrégionaux,
(a : 1 er cas (14 PSSs),
b : 2ème cas (14 PSSs), c :
3ème cas (12 PSSs)). 4.5.5.5- Discussion et
conclusion.
Rappelons que la figure (89), correspondant au choix de
sélection de chaque générateur par itération d'AG,
montre bien que les générateurs 63 et 65 ont une faible
probabilité d'être choisis pour être dotés de PSSs
par rapport aux autres générateurs. Mais lorsqu'on laisse
à l'AG la possibilité de fixer le nombre de PSSs et de
sélectionner leurs emplacements les plus efficaces, nous trouvons alors
que ces deux générateurs sont éliminés de la liste
des PSSs. La figure (102) montre la fréquence de sélection de
chaque générateur pour être doté d'un PSS pour 300
d'itérations d'AG.
L'évaluation de la fonction multiobjectif a montré
que la valeur finale est plus grande que celle du premier cas.
L'analyse des valeurs propres et des simulations dynamiques
avec 12 PSSs a montré de son côté que certains
résultats sont proches de ceux trouvés dans le 1er cas
(14 PSSs), tandis que d'autres résultats sont meilleurs. En outre, le
nombre des modes interrégionaux critiques est diminué par rapport
au 1er cas.
Rappelons que dans le 1er cas, l'optimisation a
été réalisée en traitant de façon
indépendante la localisation des PSSs et leurs paramètres. Ainsi,
l'amélioration associée au 3ème cas est obtenue par
l'optimisation simultanée de la localisation des PSSs et de leurs
paramètres. Il est aussi important de remarquer que cette méthode
a permis également de diminuer le nombre de PSSs à installer.
Cela montre par conséquent la nécessité
de prendre en considération le lieu d'emplacement des PSSs lors de
l'optimisation de leurs paramètres. Cela montre en outre la
potentialité des AGs pour réduire le nombre des PSSs tout en
gardant une bonne performance de régulation.
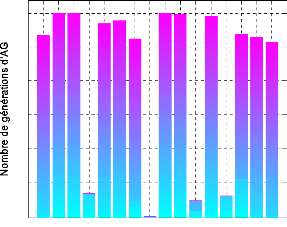
0
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
68
300
250
200
150
100
50
Numéro de générateur
Figure 102. Choix de chaque
générateur pour 300 d'itération d'AG.
4.5.6- Influence des contraintes de l'AG dans
l'optimisation : application au troisième cas. 4.5.6.1- Application des
AGs.
Sachant qu'une des caractéristiques d'un AG est la
non-production d'une solution unique pour le problème donné, tout
changement d'une contrainte de l'espace de recherche du problème ou d'un
paramètre de l'AG mène à solution différente.
Pour tester la sensibilité de la solution aux contraintes
de l'AG, nous appliquons les contraintes suivantes pour chaque PSS :
1 50
= =
K PSS j
,
0 . 0 1 0 . 1
= =
T 1 , j
0 . 0 1 0 . 1
= =
T 3 , j
{ }
5 3, ,6 8
L
{ }
0,1
PLPSS , j SWPSS , j
(150)
Nous appliquons de même les paramètres suivants de
l'AG.
|
Nombre d'individu Nind
|
100
|
|
Nombre de gènes Ngens
|
Nind × Nvar
|
|
Nombre de génération Ngener
|
300
|
|
Probabilité de croisement Pc
|
0.9
|
|
Probabilité de mutation Pm
|
0.005
|
Tableau 18. Valeurs choisies des
paramètres de l'AG.
Grâce à ces nouvelles données, l'AG
réduit le nombre de PSSs à 11 PSSs seulement. Les valeurs de
leurs paramètres sont données dans le tableau (19).
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
53
|
30.2033
|
0.0509
|
0.0499
|
|
2
|
54
|
32.1232
|
0.0523
|
0.0879
|
|
3
|
55
|
36.0024
|
0.0974
|
0.0945
|
|
4
|
57
|
04.75 19
|
0.0996
|
0.0897
|
|
5
|
58
|
06.8476
|
0.0997
|
0.0998
|
|
6
|
61
|
44.8166
|
0.0997
|
0.0804
|
|
7
|
62
|
19.2244
|
0.0116
|
0.0466
|
|
8
|
64
|
19.9228
|
0.0724
|
0.0539
|
|
9
|
66
|
46.4253
|
0.0107
|
0.0105
|
|
10
|
67
|
41.1337
|
0.0511
|
0.0929
|
|
11
|
68
|
11.7644
|
0.0345
|
0.0145
|
Tableau 19. Paramètres et
localisation des PSSs optimisés par AG.
L'évolution de la fonction multiobjectif en fonction du
nombre de générations est donnée dans ce cas à la
figure (103). Au terme de l'optimisation, la valeur finale de la fonction
multiobjectif n'atteint que 0.9614.
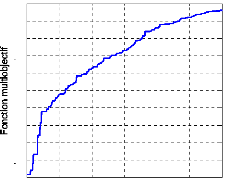
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0 0 50 100 150 200 250 300
Générations
Figure 103. Evolution de la fonction
multiobjectif.
La valeur finale de la fonction multiobjectif est
inférieure à un. Ceci nous indique que le critère de la
zone D ne sera pas assuré, même pour le point de
fonctionnement nominal. Ainsi, il faut accepter cette solution avec une
tolérance.
Nous allons dans ce qui suit analyser la performance de
régulation avec ces 11 PSSs pour le point de fonctionnement nominal
seulement car pour les autres scénarios, nous serions assez loin des
critères imposés dans cette étude.
4.5.6.2- Analyse des valeurs propres pour le point de
fonctionnement nominal.
Nous calculons les valeurs propres du système au point
de fonctionnement nominal en installant les 11 PSSs optimisés aux
emplacements déterminés par l'AG. Nous donnons dans le tableau
(20) certaines de ces valeurs propres. La figure (104) donne leurs
répartitions dans le plan complexe.
|
N° mode
|
ë
|
æ
|
f [Hz]
|
|
1
|
- 1.2324 #177; j 10.558
|
0.1159
|
1.6805
|
|
2
|
- 3.6757 #177; j 10.046
|
0.3436
|
1.5990
|
|
3
|
- 1.3897 #177; j 9.4513
|
0.1455
|
1.5042
|
|
4
|
- 1.0276 #177; j 9.3339
|
0.1094
|
1.4855
|
|
5
|
- 1.0514 #177; j 6.8663
|
0.1514
|
1.0928
|
|
6
|
- 0.8601 #177; j 7.7667
|
0.1101
|
1.2361
|
|
7
|
- 0.8629 #177; j 7.4791
|
0.1146
|
1.1903
|
|
8
|
- 2.0817 #177; j 7.5413
|
0.2661
|
1.2002
|
|
9
|
- 7.5208 #177; j 4.6996
|
0.8480
|
0.7480
|
|
10
|
- 2.1214 #177; j 3.1822
|
0.5547
|
0.5065
|
|
11
|
- 2.9320 #177; j 3.0255
|
0.6959
|
0.4815
|
|
12
|
- 0.8698 #177; j 3.9611
|
0.2145
|
0.6304
|
|
13
|
- 0. 8670 #177; j 3.7259
|
0.2266
|
0.5930
|
|
14
|
- 0.8519 #177; j 3.1696
|
0.2596
|
0.5045
|
|
15
|
- 0.9204 #177; j 2.5468
|
0.3399
|
0.4053
|
Tableau 20. Valeurs propres du
système (11 PSSs : optimisation globale par AG).
Modes locaux Modes interrégionaux


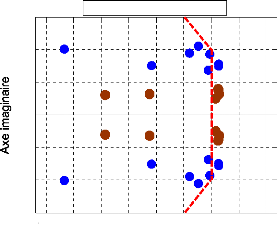
-10
-15
15
10
-5
5
0
-4 -3 -2 -1 0
-1
4ème cas , 1er scénario
dz = 10 %
Axe réel
Figure 104. Répartition des valeurs
propres du système dans le plan complexe
(11 PSSs : optimisation
globale par AG).
L'analyse des valeurs propres montre que le système se
trouve dans la zone de la stabilité. Pourtant, plusieurs modes sont
situés hors de la zone D, avec des parties réelles
supérieures à la valeur critique. Ceci ne donne pas une grande
sûreté de fonctionnement au système pour supporter des
scénarios sévères. Le facteur d'amortissement minimum est
æmin = 10.94 % et la partie réelle maximale des valeurs
propres est ómax = - 0.8519.
4.5.6.3- Analyse par simulations temporelles pour le
point de fonctionnement nominal.
La variation de vitesse des cinq générateurs
choisis pour montrer la réponse dynamique du système suite
à un défaut est donnée à la figure (105).
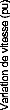
-0.005
0.005
-0.01
0.01
0
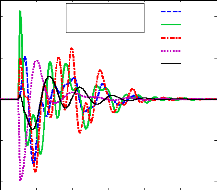
4ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
0 2 4 6 8 10 12
Temps (s)
Figure 105. Variations de vitesse des cinq
générateurs suite à un défaut de ligne,
(1er
scénario du 4ème cas).
Les valeurs caractérisant le dépassement maximum et
le temps de réponse de ces courbes sont données dans le tableau
suivant.
|
G. 53
|
G. 59
|
G. 60
|
G. 66
|
G. 68
|
|
Dp
|
5.13×10-3
|
10.7×10-3
|
5.01×10-3
|
- 9.84×10-3
|
0.49×10-3
|
|
tr (s)
|
8
|
10
|
10
|
8
|
8
|
Les réponses temporelles des angles de rotor avec le
défaut proposé et les écarts entre les angles des
générateurs (60 et 66) et (68 et 53) sont donnés
respectivement à la figure (106).
Ces analyses par simulations temporelles montrent bien que les
oscillations s'amortissent assez rapidement, au moins de 10 secondes. La
stabilité globale du système, pour ce scénario, est ainsi
assurée.
-0.5
2.5
0.5
1.5
2
0
1
4ème cas,
1er scénario
G. 53
G. 59
G. 60
G. 66
G. 68
120
100
-20
40
20
80
60
0
4ème cas,
1er scénario
(G. 60 - G. 66)
(G. 68 - G. 53)
0 2 4 6 8 10 12
Temps (s)
0 2 4 6 8 10 12
Temps (s)
a b
Figure 106. Réponse dynamique des
générateurs (1er scénario du
4ème cas),
a : angles de rotor,
b : écart des angles de deux paires.
4.5.6.4- Discussion et conclusion.
D'un point de vue général, le fait de disposer
d'un ensemble de solutions est une source de richesse permettant au concepteur
de bénéficier d'une base solide pour choisir, a
posteriori, une solution parmi celles proposées, ou pour parfaire
la conception. La multiplicité des solutions favorise également
l'identification des zones optimales les plus intéressantes (ou les
moins contraignantes) pour certains éléments du système ou
certains critères particuliers non- intégrés au
problème d'optimisation tels le coût, ... .
Dans notre cas, la solution que nous avons obtenue avec 11
PSSs présente un côté positif d'un point de vue
économique (par la réduction de leur nombre) et un
côté négatif par un manque de robustesse (par le
non-respect des critères de stabilité). Dans le cas des PSS, le
coût des ces derniers ne représente pas un enjeu critique. Par
contre la priorité essentielle concerne la stabilité du
système pour le plus grand nombre possible des scénarios. Ainsi,
la zone de la robustesse étant la plus importante, la solution des 11
PSSs doit être moins favorisée.
4.6- Conclusion.
Les études menées au cours de ce chapitre ont
permis de mettre en évidence les avantages de notre approche, celle-ci
permettant d'améliorer simultanément l'amortissement des modes
des oscillations électromécaniques globales et locales par une
optimisation globale des PSSs.
Quatre cas ont été étudiés.
Dans le 1 er cas, nous avons utilisé la
méthode des facteurs de participation pour localiser les PSSs
nécessaires au système et la méthode des AGs a
été utilisée pour régler les paramètres de
ces PSSs. Nous avons comparé les résultats obtenus, pour le point
de fonctionnement nominal, avec ceux issus d'une méthode d'optimisation
classique (la méthode de compensation de phase) et d'une méthode
métaheuristique (algorithme d'optimisation par essaim de particules) et
les résultats de la littérature. Les résultats obtenus
avec notre méthode d'AG montrent que la performance du réglage du
système est efficace, avec un bon
amortissement pour tous les modes. Par ailleurs, nous avons
remarqué que la performance s'est dégradée pour les autres
scénarios (défauts sévères). La robustesse du
réglage n'est donc pas suffisamment assurée dans ce cas.
Dans le 2ème cas, nous avons
déterminé en outre l'emplacement des PSSs par l'AG, le nombre des
PSSs utilisé étant préfixé. L'analyse des
résultats obtenus montre la supériorité de cette approche
par rapport à la méthode classique des facteurs de participation.
Nous avons obtenu des performances qui améliorent, par exemple, de 40 %
les temps de réponse des générateurs pour tous les
scénarios étudiés. Quant à l'amortissement de tous
les modes interrégionaux, il est notablement augmenté.
Dans le 3ème cas, nous avons axé
notre recherche sur l'optimisation du nombre des PSSs. Nous avons
considéré que ce paramètre est très important pour
minimiser les interactions nuisibles entre PSSs. Nous avons ainsi
développé l'approche correspondante. Les résultats obtenus
montrent que la stabilité globale du système est garantie. Le
nombre de modes interrégionaux critiques est diminué par rapport
au 1er cas malgré la réduction du nombre de PSSs (12
PSSs contre 14).
Dans le 4ème cas, nous avons
évalué la sensibilité des AGs vis-à-vis des
paramètres de réglage telles la probabilité de croisement
et les contraintes de l'espace de recherche. La "désensibilisation" de
l'AG par rapport aux contraintes de l'espace de recherche du problème
étudié fera l'objet du chapitre suivant.
Enfin nous pouvons conclure qu'outre l'optimisation
coordonnée des paramètres des PSSs souvent appliquée dans
le réglage des PSSs, il faut aussi tenir compte du nombre et de la
localisation optimale de ces PSSs pour pouvoir réduire au maximum les
effets indésirables des interactions entre PSSs. La stabilité
globale du système peut alors être correctement assurée par
une optimisation simultanée des paramètres et de leur emplacement
avec un nombre réduit de PSSs.
| 

