Chapitre V
Optimisation par
algorithmes génétiques
à
contraintes dynamiques
5.1- Introduction.

x
Dans la littérature, plusieurs méthodes sont
proposées pour améliorer la performance des AGs, dans la
recherche de l'optimum global, telles les méthodes des opérateurs
génétiques auto-adaptatifs (Bäck, 1992; Angeline, 1995; Deb,
1999; Régnier, 2003), la parallelisation des AGs (Alba et al.,
1999; Tomassini, 1999; Hongesombut et al., 2005), ... . Ces
méthodes présentent de bons résultats, mais si le point
optimal global cherché ne se trouve pas dans l'espace de recherche
proposé du problème (figure (107)), ces méthodes ne
permettent pas aux AGs de trouver ce point.
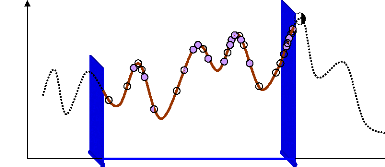
f(x)
OG
xmin xmax
Figure 107. Problème d'optimum
global situé en dehors de l'espace de recherche proposé.
Le bon déroulement d'un programme d'AG dépend de
la détermination de l'espace de recherche, borné par une valeur
maximale et minimale, associées à chaque paramètre
à optimiser.
L'espace de recherche du problème définissant un
ensemble des solutions potentielles peut ainsi contenir la solution optimale
globale et/ou d'autres solutions locales. Ainsi, pour l'obtention de l'optimum
global, il est alors très important de bien déterminer cet espace
de recherche, autrement dit il faut bien choisir ses contraintes.
Dans la plupart des problèmes d'optimisation, il n'y a
pas de critères rigoureux pour déterminer
précisément les contraintes de l'espace de recherche. Dans la
pratique, le choix de ces contraintes reste ainsi arbitraire.
Lors de l'optimisation de problèmes à grand
nombre de paramètres tels les PSSs, il est souvent très difficile
de déterminer pour des paramètres de même type (constantes
de temps, gains, ....) des espaces de recherche différents. Ainsi, ces
espaces de recherche sont généralement fixés par
l'expérience et le savoir faire ; ils ont souvent des valeurs
identiques. Ces espaces restent enfin fixes tout au long du processus
d'optimisation. Ainsi, la valeur d'un paramètre peut atteindre une des
limites de l'espace de recherche associé. Le fait d'atteindre cette
limite peut arriver après un certain nombre de générations
ou même dès le début de l'optimisation. Par
conséquent, l'évolution de la fonction objectif peut se
décélérer, voire se stabiliser, bien avant de converger
vers la solution optimale.
Une solution peut être proposée pour
améliorer la convergence de l'algorithme et la qualité de la
solution optimale recherchée. Cette solution est basée sur la
libération des contraintes de l'espace de recherche au cours de
l'application de l'AG qui permet de leur donner des valeurs différentes
selon les besoins du processus d'optimisation. Nous permettons ainsi à
l'AG de diversifier sa population par de nouvelles valeurs qui n'étaient
pas accessibles avec un espace de recherche fixe. Nous réalisons donc un
espace de recherche dynamique qui s'adapte à la recherche de l'optimum
global.
Nous allons dans ce chapitre appliquer cette approche à
l'optimisation des PSSs. 5.2- Approche proposée.
Rappelons que la forme générale d'un
problème d'optimisation (maximisation) est :
max( ( )) : R ? R (151)
F X n k
X S
?
· { } n
X = x 1 , x 2 ,
L , x n ? R : vecteur des paramètres à optimiser de
dimension n.
· { } k
F = f 1 , f 2 ,
L , fn ? R : fonction objectif de dimension n.
Pour k = 1, le problème est dit monoobjectif, autrement il est
multiobjectif.
· n
S ? R : espace de recherche du problème a des
contraintes aux limites. Les points de cet espace de recherche doivent
correspondre à des solutions réalisables. Les contraintes
définissants ses limites peuvent être données par des
valeurs minimales xi,min et maximales xi,max
associées à chaque paramètre à optimiser :
x i x i x i i { n}
,mi n ,max : 1,2 ,
= = = L(152)
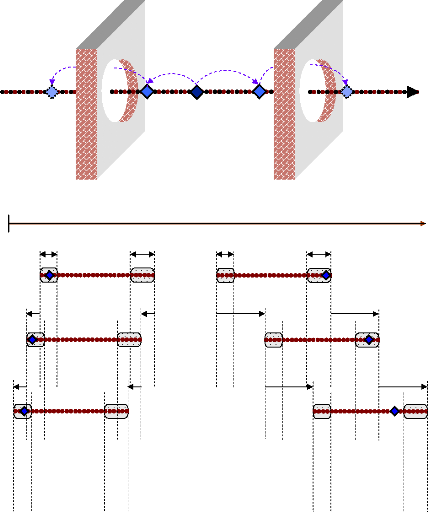
Les figures (108) et (109) donnent respectivement le principe
général et l'organigramme de l'approche proposée. Dans
cette approche, nous initialisons l'AG avec un espace de recherche fixe.
Lorsque l'évolution de la fonction objectif ne s'améliore plus de
façon significative, nous utilisons alors des contraintes dynamiques sur
l'espace de recherche. Une marge de tolérance
(åm, ån) est fixée
pour chacune des deux extrémités de l'espace de recherche.
Lorsque la valeur d'un paramètre atteint cette marge pendant un certain
nombre de générations successives (Ng), les limites
associées à l'espace de recherche de ce paramètre vont
être modifiées par des valeurs prédéterminées
(Äm, Än). L'espace de
recherche du paramètre se déplacera en gardant toujours sa taille
initiale. Ce processus peut se répéter plusieurs fois au cours de
l'optimisation. Enfin, pour que les valeurs attribuées aux
paramètres soient des solutions réalisables (valeurs positives
dans notre cas), il faut limiter l'évolution des valeurs minimales de
l'espace de recherche à une valeur faible (åp
> 0).
An
An
An
An
xmin xmax
åm
xmax
0
xmin
ån
x
x
xmin
xmax
ån
åm
Am
Am
Am
Am
Figure 108. Le principe
général de l'approche des contraintes dynamiques.
Pour i = 1 : Nvar
Non
xi,max = xi,max +
Äm
xi,min = xi,min +
Äm
Si xi > xi,max -
åm
Oui
Opérateurs d'AG
Si Gener > = Nd
Pour j = 1 : Ng
xi,max = xi,max
xi,min =
xi,min
Si xi < xi,min -
ån & xi > åp
Oui
xi,min = xi,min -
Än
xi,max = xi,max -
Än
Oui
Non
Non
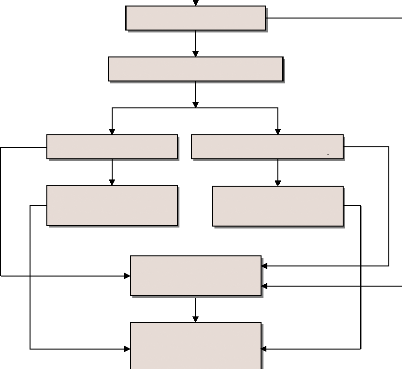
Figure 109. Organigramme de l'approche des
contraintes dynamiques. 5.3- Première
application.
Nous appliquons l'approche au premier cas étudié
dans le chapitre précédent. 5.3.1- Optimisations par
contraintes fixes.
Les espaces de recherche utilisés dans l'optimisation
des PSSs disposent des contraintes fixes tout au long du processus
d'optimisation. Ces espaces de recherche (pour les trois paramètres
(KPSS,i, T1,i, T3,i) à
optimiser par PSS) sont soumis aux contraintes données par la relation
(144). Les valeurs choisies des paramètres de l'AG sont donnés au
tableau (7).
L'évolution de la fonction multiobjectif en fonction du
nombre de générations a été déjà
donnée à la figure (61). Nous remarquons que la valeur finale de
la fonction multiobjectif, atteinte pour la génération maximale
prédéterminée de 250, est de 1.097.
La figure (110) montre la variation, pour chaque
génération de l'AG, des valeurs des trois paramètres
choisis (KPSS (13), T1 (14), T3 (9)).
40
39
38
37
36
35
0 50 100 150 200 250
a
Génération
0.1
0.08
0.06
0.04
0.02
0.001
0.04
0.03
0.02
0.01
0.001
0 50 100 150 200 250
Génération 0 50 100 150 200 250
Génération
b c
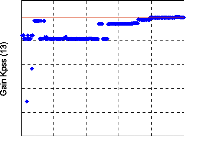
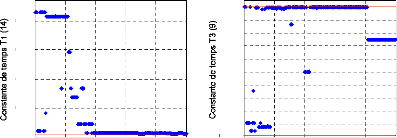
Figure 110. Variation des valeurs des
trois paramètres (a : KPSS (13), b :
T1 (14), c : T3 (9)).
Sur cette figure, nous pouvons remarquer les points suivants :
- Le gain du 1 3ème PSS converge, à
partir de la 1 80ème génération, vers une
valeur très proche de la limite maximale de l'espace de recherche
associé.
- La constante de temps T1 du 14ème
PSS converge, à partir de la 100ème
génération, vers une valeur très proche de la limite
minimale de l'espace de recherche associé.
- La constante de temps T3 du 9ème
PSS atteint dès la 40ème génération une
valeur très proche de la limite maximale de l'espace de recherche
associé. Au-delà de la 200ème
génération, elle atteint une autre valeur située loin des
limites de l'espace de recherche.
Rappelons que la répartition des modes
électromécaniques du système dans le plan complexe,
donnée à la figure (63), montre que tous les modes
électromécaniques, sauf deux d'entre eux, sont
déplacés dans la zone D de stabilité ; le facteur
d'amortissement minimum est æmin = 15.02 % et la partie
réelle maximale des valeurs propres est ómax = -
0.9485.
5.3.2- Optimisations par contraintes
dynamiques.
Nous appliquons maintenant l'approche proposée pour
optimiser les paramètres des 14 PSSs, avec des espaces de recherche
modifiables tout au long du processus d'optimisation.
Les contraintes initiales des espaces de recherche et les valeurs
choisies des paramètres de l'AG sont les mêmes que
précédemment (relation (144) et tableau (7) respectivement).
Sur la figure (61), nous remarquons que l'évolution de
la fonction multiobjectif s'arrête généralement de
s'améliorer d'une façon significative à partir de la
75ème génération. Nous pouvons donc
considérer que cette génération (Nd = 75) est le
point de départ des contraintes dynamiques.
Les marges de tolérance (åm,
ån) des deux extrémités de l'espace de
recherche de chaque paramètre sont choisies comme suit :
( ) 1 , ( ) 0 . 05
K K
PSS i n PSS i
, ,
å m
= =
å
|
å m
|
( ) 0 .0 1 , ( )
T T
1 , 1 ,
i n i
= å
|
0.0005
|
(153)
|
å m (T3
, 1 ,
i n i
) 0. 0 1 , ( ) 0 . 0005
= =
å T
Le nombre des générations successives
nécessaire pour permettre aux contraintes de changer leurs valeurs est
déterminé à Ng = 50.
Les valeurs de changement possible des contraintes
(Äm, Än) sont choisies, quant
à elles, comme suit :
Äm
( ) 2 , ( ) 0 . 05
K K
PSS i n PSS i
, ,
= Ä =
|
Äm
|
( ) 0 . 0 1 , ( )
T T
1 , 1 ,
i n i
= Ä
|
0.0005
|
(154)
|
Äm (T3
, 1,
i n i
) 0. 0 1 , ( ) 0 . 0005
= Ä =
T
L'évolution de la fonction multiobjectif en fonction du
nombre de générations est donnée à la figure
(111).
0 50 100 150 200 250
Generations
Figure 111. Evolution de la fonction
multiobjectif.
Sur cette figure, nous constatons que la fonction
multiobjectif atteint une valeur égale à la valeur finale du cas
précédent, soit 1.097, pour la génération 120.
Ensuite, elle atteint la valeur de 1.234 pour la génération
maximale prédéterminée de 250. Ainsi, par rapport au cas
précédent, la convergence est assurée en moins de 130
générations. Au bout de 250 générations, nous
obtenons un gain de 12,4 %.
Les valeurs optimales des paramètres des PSSs sont
données au tableau (21).
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
54
|
37.7248
|
0.0790
|
0.0452
|
|
2
|
55
|
23.4329
|
0.0238
|
0.0441
|
|
3
|
56
|
33.6390
|
0.0637
|
0.0462
|
|
4
|
57
|
32.2578
|
0.0673
|
0.0460
|
|
5
|
58
|
38.3750
|
0.0608
|
0.0850
|
|
6
|
59
|
23.0859
|
0.0851
|
0.0809
|
|
7
|
60
|
01.5685
|
0.0862
|
0.0812
|
|
8
|
61
|
12.6048
|
0.0098
|
0.0293
|
|
9
|
62
|
10.4482
|
0.0398
|
0.1051
|
|
10
|
63
|
14.6773
|
0.0511
|
0.0755
|
|
11
|
64
|
23.7698
|
0.0552
|
0.1231
|
|
12
|
65
|
16.5094
|
0.0039
|
0.0143
|
|
13
|
67
|
43.8539
|
0.0090
|
0.0081
|
|
14
|
68
|
34.4827
|
0.0048
|
0.0003
|
Tableau 21. Paramètres des PSSs
optimisés par AG à contraintes dynamiques. Les valeurs des
paramètres fixés des PSSs sont les mêmes que le cas
précédent : Tw,j = 10 et T2,j = T4,j =
0.02.
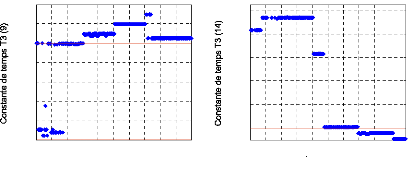
Pour montrer l'évolution des valeurs des
paramètres des PSSs lors de l'optimisation, nous donnons à la
figure (112) la variation des trois paramètres les plus
représentatifs (KPSS (13), T3 (9),
T3 (14)) pour chaque génération d'AG.
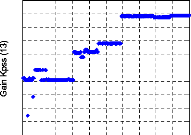
Sur cette figure, nous pouvons remarquer les points suivants :
- Le gain du 13ème PSS prend, à partir
de la 75ème génération, de nouvelles valeurs
plus
élevées que la limite maximale initiale. La valeur
finale atteinte est de 43.853.
- La constante de temps T3 du 9ème
PSS dépasse aussi sa limite maximale initiale. Sa
valeur optimale est de 0.1231.
- La constante de temps T3 du 14ème
PSS atteint, à partir de la 120ème
génération, une valeur très proche de sa limite minimale
initiale. Ensuite, elle prend des valeurs inférieures à cette
limite. Elle atteint au bout de l'optimisation la valeur 0.0003.
44
42
40
38
36
a
0 50 100 150 200 250
Génération
0.001
0 50 100 150 200 250
Génération
0 50 100 150 200 250
Génération
0.14
0.011
0.12
0.009
0.1
0.08
0.007
0.06
0.005
0.04
0.003
0.02
0.001
b c
Figure 112. Variation des valeurs des trois
paramètres (a : KPSS (13), b : T3
(9), c : T3 (14)).
Un indice intéressant, défini par la relation
suivante (Wood, 2006), permet de comparer les deux résultats. Il s'agit
du rendement ç de la valeur optimale de la fonction
multiobjectif (Fobjmax) pour la génération courante
itr :
Fobj itr
ç (155)
= ( max ) · 100 %
itr
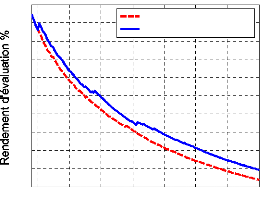
Nous pouvons ainsi tracer l'évolution de ce rendement
pour les deux résultats (optimisation par contraintes fixes et
dynamiques), figure (113). L'analyse de cette figure montre qu'au-delà
de la 150ème génération, le rendement est quasi
linéaire. Un gain de 25 générations est constaté
pour une valeur fixée du rendement.
Pour évaluer la performance du réglage des PSSs
sur le système étudié, nous montrons par la figure (114)
la répartition des modes électromécaniques du
système dans le plan complexe. Tous les modes
électromécaniques sont bien déplacés dans la zone
D de stabilité ; cela traduit bien l'amélioration
réalisée sur l'optimisation de la fonction multiobjectf. Le
facteur d'amortissement minimum est æmin = 14.82 % et la partie
réelle maximale des valeurs propres est ómax = -
1.085.
0.4
75 100 125 150 175 200 225 250
1.4
Contraintes fixes Contraintes dynamiques
1.2
1
0.8
0.6
Génération
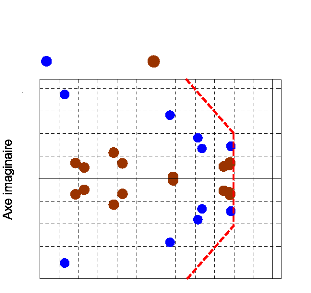
Figure 113. Evolution du rendement de la
fonction multiobjectif.
Modes locaux Modes interrégionaux
20
dz = 10 %
10
0
-10
-20
-6 -5 -4 -3 -2 - 0
-1
Axe réel
Figure 114. Valeurs propres du
système.
Les résultats obtenus montrent que l'approche
proposée a élargi l'espace de recherche initial de certains
paramètres. En prenant maintenant un espace de recherche initial aussi
étendu que celui obtenu par l'approche à contraintes dynamiques,
nous vérifions son évolution par l'AG à contraintes fixes.
Nous appliquons ainsi les contraintes fixes suivantes :
|
0.1 45
= =
K PSS j
,
0.0005 0 . 1 3
= =
T 1 , j
0.0005 0 . 1 3
= =
T 3 , j
|
(156)
|
|
avec
|
j
|
1,2,
|
|
, NPSS
|
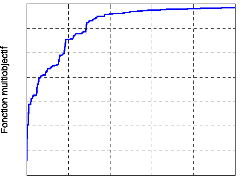
L'évolution de la fonction multiobjectif correspondante
en fonction du nombre de générations, (figure (115)), montre que
la valeur atteinte au bout de l'optimisation est égale seulement
à 0.984. Par conséquent, nous trouvons que ce résultat est
inférieur à celui obtenu par l'optimisation à contraintes
dynamiques. En effet, le fait d'élargir l'espace de recherche de tous
les paramètres du problème restreint la recherche du point
optimal : plus l'espace de recherche est large, plus la possibilité
d'être piégé par les optima locaux est grande.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3 0 50 100 150 200 250
Générations
Figure 115. Evolution de la fonction
multiobjectif.
Au-delà de ces résultats et pour montre
l'efficacité de notre approche des contraintes dynamiques, nous
proposons de l'appliquer sur un petit espace de recherche se trouvant assez
loin de la solution optimale que nous avons déjà
trouvée.
Nous prenons, par exemple, la moitié de l'espace de
recherche initial identifié par la relation (144), soit l'espace
donné par la relation (157). En optimisant, en premier lieu, les
paramètres des PSSs avec contraintes fixes, nous trouvons que la
fonction multiobjectif converge à une valeur trop faible, soit 0.5 13,
figure (116).
0.1 20
,
= =
K PSS j
0 . 00 1 0 .05
= =
T 1 , j
0 . 00 1 0 . 05
= =
T 3 j
,
(157)
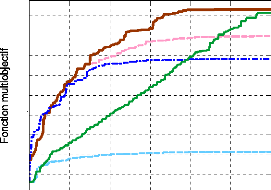
Par contre, lors de l'application des contraintes dynamiques,
l'espace de recherche s'élargit successivement et la valeur de la
fonction multiobjectif s'améliore jusqu'à l'arrivée
à une valeur très proche de la solution optimale trouvée
précédemment, soit 1.225, figure (116).
1.2
1.1
1
0.9
0.8
0.7
0.6
0.5
0.4
0 50 100 150 200 250 300
Générations
Espace de recherche initial
Demi-espace de recherche

Contraintes fixes Contraintes dynamiques

Contraintes fixes Contraintes dynamiques
Espace de recherche élargi

Contraintes fixes
Figure 116. Evolution de la fonction
multiobjectif des résultats de la 1ère
application.
Nous résumons dans le tableau suivant l'ensemble des cinq
résultats d'AG obtenus avec : - l'espace de recherche initial à
contraintes fixes (ERICF).
- l'espace de recherche à contraintes dynamiques
(ERCD).
- l'espace de recherche élargi à contraintes fixes
(ERECF).
- la moitié de l'espace de recherche initial à
contraintes fixes (MERICF).
- la moitié de l'espace de recherche à contraintes
dynamiques (MERCD).
|
ERICF
|
ERCD
|
ERECF
|
MERICF
|
MERCD
|
|
Valeur finale de la
fonction multiobjectif
|
1.097
|
1.234
|
0.984
|
0.513
|
1.222
|
|
Valeur finale relative %
(par rapport à l'ERICF)
|
_____
|
12.4 %
|
? 10.3 %
|
? 53.2 %
|
11.4 %
|
|
Taux de convergence %
(par rapport à l'ERICF)
|
_____
|
- 52 %
|
non-
convergeant
à 1.097
|
non-
convergeant
à 1.097
|
- 6 %
|
Tableau 22. Résultats de la
1ère application.
En analysant ces résultats nous pouvons dire que :
- Vu le nombre important des paramètres à
optimiser (42 paramètres dans ce cas), il très difficile de
donner à chaque paramètre un espace de recherche
différent. Nous les proposons donc identiques.
- Dans le cas de l'optimisation avec espace de recherche fixe
; si la taille de cet espace est faible, il y a très peu de chance qu'il
contienne la meilleure solution du problème. On converge souvent vers un
optimum local.
- D'autre part, si l'espace de recherche fixe est très
large ; l'exploration et l'exploitation de cet espace risquent de ne pas
être efficaces. L'optimisation, dans ce cas, est souvent
piégée par un optimum local.
- Par contre, lors de l'utilisation des contraintes
dynamiques, seuls les paramètres qui ne trouvent pas leurs valeurs
optimales dans l'espace de recherche initial vont évoluer pour prendre
des valeurs supérieures ou inférieures. Cela se traduit donc par
une convergence rapide vers la solution optimale, avec une amélioration
de la robustesse de l'AG et de la performance de l'optimisation.
5.4- Deuxième application.
Nous allons maintenant valider notre approche pour un autre cas
d'optimisation. Nous l'appliquons au troisième cas (12 PSSs).
5.4.1- Optimisations par contraintes fixes.
Rappelons que l'optimisation des PSSs du troisième cas,
par contraintes fixes, a été faite dans le chapitre
précédent (§§-5.5.1). Les espaces de recherche des 12
PSSs à optimiser par PSS sont soumis aux contraintes données par
la relation (149). Les paramètres du réglage de l'AG sont
donnés au tableau (14).
L'évolution de la fonction multiobjectif en fonction du
nombre de générations est donnée à la figure (91).
Sur cette figure, nous remarquons que la fonction multiobjectif atteint la
valeur finale, soit 1.223, pour la génération maximale
prédéterminée de 300.
Rappelons aussi que la répartition des modes
électromécaniques du système dans le plan complexe est
donnée à la figure (93). Cette dernière montre que tous
les modes dominants se trouvent dans la zone D de stabilité ;
le facteur d'amortissement minimum est æmin = 13.96 % et la
partie réelle maximale des valeurs propres est ómax = -
1.0836.
5.4.2- Optimisations par contraintes
dynamiques.
Comme nous l'avons proposé dans cette nouvelle
approche, le processus d'optimisation est initialisé par les contraintes
des espaces de recherche fixes (relation (149)). Les paramètres de
réglage choisis pour l'AG restent les mêmes, (tableau (14)).
La figure (91) représentant l'évolution de la
fonction multiobjectif montre que, à partir de la
120ème génération, cette fonction ne
s'améliore plus d'une façon "importante". Les contraintes
dynamiques sont appliquées à partir de cette
génération, (Nd = 120).
Les marges de tolérance (åm,
ån) des deux extrémités de l'espace de
recherche de chaque paramètre sont choisies comme suit :
|
å å
m PSS i n PSS i
( ) 1 , ( ) 0 .2
K K
, ,
= =
å å
m i n i
( ) 0. 0 1 , ( ) 0 . 002
T T
1 , 1 ,
= =
|
(158)
|
|
å å
m i n i
( ) 0 . 0 1 , ( )
T T
3 , 1 ,
=
|
0.002
|
Le nombre des générations successives
nécessaire pour permettre aux contraintes de changer leurs valeurs est
déterminé à Ng = 20.
Les variations possibles des contraintes
(Äm, Än) sont choisies, quant
à elles, comme suit : ( ) 2 , ( )
Äm
0.2
K K
PSS i n PSS i
, ,
= Ä
|
Äm
|
( ) 0 . 02 , ( )
T T
1 , 1 ,
i n i
= Ä
|
0.002
|
(159)
|
Äm (T3
, 1,
i n i
) 0. 02 , ( ) 0 . 002
= Ä =
T
Les valeurs optimales des paramètres des PSSs sont
données au tableau (23).
|
N° PSS
|
N° G.
|
KPSS
|
T1
|
T3
|
|
1
|
53
|
22.7145
|
0.0715
|
0.1371
|
|
2
|
54
|
36.6309
|
0.0369
|
0.0450
|
|
3
|
55
|
34.2725
|
0.0953
|
0.0889
|
|
4
|
57
|
01.8484
|
0.0869
|
0.0689
|
|
5
|
58
|
28.9526
|
0.0864
|
0.0397
|
|
6
|
59
|
11.5439
|
0.0712
|
0.0398
|
|
7
|
61
|
45.8373
|
0.0529
|
0.1102
|
|
8
|
62
|
20.5999
|
0.0149
|
0.0494
|
|
9
|
64
|
17.9713
|
0.0466
|
0.0452
|
|
10
|
66
|
49.3448
|
0.0192
|
0.0179
|
|
11
|
67
|
43.6407
|
0.0044
|
0.03 11
|
|
12
|
68
|
39.1085
|
0.0506
|
0.0793
|
Tableau 23. Paramètres des PSSs
optimisés par AG à contraintes dynamiques. Les valeurs des
paramètres fixés des PSSs sont les mêmes que le cas
précédent : Tw,j = 10 et T2,j = T4,j =
0.02.
L'évolution de la fonction multiobjectif en fonction du
nombre de générations est donnée à la figure
(117).
|
1.4
1.2
1 0.8 0.6 0.4 0.2
0
|
|
0 50 100 150 200 250 300
Génerations
Figure 117. Evolution de la fonction
multiobjectif.
Nous présentons dans le tableau suivant les
résultats de l'AG obtenus dans cette application avec :
- l'espace de recherche à contraintes fixes (ERCF).
- l'espace de recherche à contraintes dynamiques
(ERCD).
|
ERCF
|
ERCD
|
|
Valeur finale de la fonction
multiobjectif
|
1.223
|
1.387
|
|
Valeur finale relative %
(par rapport à l'ERCF)
|
_____
|
13.4 %
|
|
Taux de convergence %
(par rapport à l'ERCF)
|
_____
|
- 30 %
|
Tableau 24. Résultats de la
2ème application.
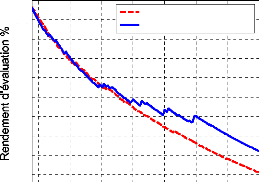
Comme dans la 1ère application (relation
(155)), la figure (118) montre qu'à partir de la
175ème génération, un gain progressif du nombre
de générations est constaté par l'optimisation à
contraintes dynamiques. Le gain maximum, pour une valeur fixée du
rendement, est de 35 générations.
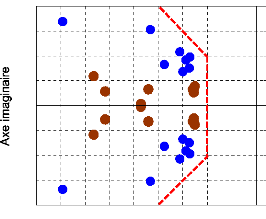
La répartition des modes
électromécaniques du système équipé des 12
PSSs optimisés est donnée à la figure (119). Cette figure
montre clairement que tous les modes électromécaniques du
système sont bien déplacés dans la zone D de
stabilité. Le facteur d'amortissement minimum et la partie réelle
maximale des valeurs propres sont respectivement æmin = 13.74 %,
ómax = - 1.249. Ce résultat d'optimisation garantit la
stabilité globale du système et une performance robuste pour un
grand nombre de scénarios.
0.8
Contraintes fixes Contraintes dynamiques
0.7
0.6
0.5
0.4
125 150 175 200 225 250 275 300
Génération

Figure 118. Evolution du rendement de la
fonction multiobjectif.
Modes locaux Modes interrégionaux
20
dz = 10 %
10
0
-10
-4 -3 -2 -1 0
-1
-20
Axe réel
Figure 119. Valeurs propres du
système.
5.5- Conclusion.
Dans ce chapitre, nous avons proposé une approche
d'optimisation d'AG à contraintes dynamiques permettant la recherche du
point optimal du problème hors des contraintes initiales de l'espace de
recherche.
Pour mettre en évidence l'apport de cette approche,
nous l'avons appliquée à l'optimisation des PSSs. Nous avons
également comparé les résultats obtenus avec ceux de l'AG
à contraintes fixes.
Par rapport à l'optimisation utilisant l'AG à
contraintes fixe, l'analyse des résultats obtenus montre que la nouvelle
approche assure :
- une amélioration de la valeur finale de la fonction
multiobjectif (plus de 12 % dans les deux cas étudiés).
- une accélération de la convergence (plus de 30 %
sur le nombre de générations, dans les deux cas
étudiés).
Par conséquent, cette amélioration de la
fonction multiobjectif conduit à une meilleure stabilité globale
du système. Elle garantit aussi une bonne performance du système
pour divers points de fonctionnement et scénarios.
En conclusion, nous pouvons dire qu'il est possible de bien
améliorer la convergence de l'AG et la performance de son
résultat. Cela améliore en outre la robustesse de l'AG et sa
désensibilisation vis-à-vis de l'espace de recherche
proposé.
De ce fait, l'approche de l'AG à contraintes dynamiques
ouvre des nouvelles possibilités dans l'utilisation des AGs.
| 


