Memoire Online - Etude de la stabilité aux petites perturbations dans les grands réseaux électriques: Optimisation de la régulation par une méthode metaheuristique

Au fil des années, de nombreuses recherches ont été effectuées et de nombreuses approches ont été proposées pour effectuer le meilleur réglage et coordination des PSSs.

Dans les systèmes de puissance, nous avons besoin d'installer plusieurs PSSs. Traditionnellement, les paramètres de ces PSSs sont réglés séquentiellement et séparément (Abe et al., 1983; Arredondo, 1997; Yee et al., 2004). Dans les stratégies de réglage séquentiel, basées sur les méthodes de réglage présentées dans le chapitre précédent, les PSSs sont alors conçus pour amortir les oscillations des modes, mode par mode. Par exemple, la méthode linéaire séquentielle (Linear Sequential Method, LSM) est basée sur les résidus. Dans cette méthode, les PSSs sont réglés d'une manière progressive (Yee et al., 2004) :

- on calcule tout d'abord les résidus de la fonction de transfert du système en boucle

ouverte. Puis un PSS est ajouté et réglé en utilisant les informations de ces résidus.

- ensuite, un second PSS est introduit et réglé en se basant sur les informations des

- ce processus continue jusqu'à ce que le système atteigne des caractéristiques de stabilité satisfaisantes.

Une autre méthode séquentielle basée sur le placement des pôles du système est connue sous le nom : positionnement séquentiel des valeurs propres (Sequential Eigenvalue Assignment) (Fleming et al., 1981). Dans cette méthode, les paramètres des PSSs sont représentés comme des variables dans les équations caractéristiques du système. Ces équations sont résolues itérativement jusqu'à ce que les valeurs propres se trouvent placées aux endroits déterminés préalablement. La solution représente les paramètres des PSSs recherchés. Comme les "bonnes" valeurs propres spécifiées sont souvent choisies par expertise, les valeurs déterminées des paramètres des PSSs peuvent être situées en dehors de gammes correspondantes de fonctionnement (Hong et al., 1999). De ce fait, la méthode doit être appliquée de façon itérative jusqu'à obtenir des paramètres adéquats.

Bien que les méthodes de réglage séquentiel soient simples et aient donné généralement des résultats satisfaisants pour l'amortissement des oscillations, ces méthodes ne peuvent assurer une optimisation globale des PSSs et, ainsi, la stabilité globale du système. Les aspects négatifs de ces méthodes sont liés aux hypothèses restrictives et à la nature intuitive du processus de réglage (Fleming et al., 1981). En outre, les interactions dynamiques entre les différents modes ont une influence significative sur le réglage des PSSs : le réglage d'un PSS pour stabiliser un mode peut ainsi produire des effets opposés sur les autres modes.

La littérature montre qu'à la place des méthodes de réglage séquentiel, une optimisation simultanée des PSSs du système entier peut être utilisée (CIGRE, 1999). Les méthodes d'optimisation simultanée peuvent permettre d'atteindre plusieurs objectifs :

- un bon fonctionnement du système de puissance avec un amortissement satisfaisant pour diverses conditions de fonctionnement et configurations du système.

Grâce à la rapidité du développement de l'informatique, l'utilisation des outils et des algorithmes d'optimisation devient de plus en plus aisée et efficace. Cette révolution informatique a permis une ouverture vers des méthodes synthétiques telles les méthodes d'optimisation stochastiques. A la différence des méthodes analytiques dans lesquelles on

cherche à trouver une solution théorique exacte ou une bonne approximation numérique, les méthodes stochastiques constituent une approche originale dans laquelle on cherche à trouver des solutions satisfaisant aux mieux différents critères souvent contradictoires. Elles peuvent aussi synthétiser des solutions nouvelles et originales sans idées préconçues.

La résolution d'un problème d'optimisation consiste à explorer un espace de recherche afin d'optimiser (maximiser ou minimiser) une fonction donnée (une fonction objectif) sous certaines contraintes. La complexité du problème, en taille ou en structure, relative à l'espace de recherche et à la fonction à optimiser conduit à développer diverses méthodes. Ces méthodes peuvent être regroupées en deux catégories : les méthodes déterministes (classiques) et les méthodes non-déterministes (stochastiques).

Ces méthodes, qualifiées de stochastiques, sont bien adaptées aux problèmes importants et complexes (tels les problèmes discrets) ou même à des problèmes ayant des multifonctions objectif. Dans cette famille de méthodes, on parle couramment d'heuristique et de métaheuristiques.

Une méthode heuristique est une méthode d'optimisation adaptée à un problème particulier. Parmi ces méthodes, figurent la méthode de Monte-Carlo, le recuit simulé, la recherche tabou, la méthode de descente, ... . Ces diverses méthodes travaillent toujours à partir d'une solution initiale en essayant de l'améliorer au maximum en fonction des contraintes du problème étudié. Ainsi, elles ont toutes un point commun : à savoir leurs itérations reposent sur l'amélioration d'une solution unique. Leurs évolutions sont ainsi basées sur la notion de parcours : l'évolution vers une solution optimale se fait en testant successivement une solution voisine de la solution courante. La figure (38) illustre une représentation simple d'une méthode d'optimisation à parcours (heuristique).

Une méthode métaheuristique consiste en une stratégie de choix pouvant piloter une ou plusieurs heuristiques de manière abstraite, sans faire appel à un problème spécifique. Les méthodes métaheuristiques sont ainsi des méthodes à population de solutions : à chaque itération, elles manipulent un ensemble de solutions en parallèle (Osman et al., 1996). Ces

méthodes sont aussi considérées comme des méthodes d'optimisation globale : elles visent la détermination de l'optimum global de la fonction objectif du problème, en évitant le "piégeage" dans l'un de ses optima locaux. Elles comblent ainsi le handicap des méthodes classiques et des méthodes heuristiques en conduisant la recherche vers l'optimum global. En outre, ces méthodes font usage de l'expérience accumulée durant la recherche de l'optimum, pour mieux guider la suite du processus de recherche. Elles permettent ainsi d'explorer et d'exploiter l'espace de recherche plus efficacement. Une représentation schématique simple des métaheuristiques est donnée à la figure (39).

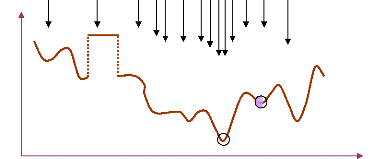
Dans cette représentation, les métaheuristiques (MH) tentent de trouver l'optimum global (OG) d'un problème d'optimisation (f(x)) difficile (avec par exemple des discontinuités (DC)), sans être piégé par les optima locaux (OL).

Les algorithmes évolutionnaires regroupent une multitude de métaheuristiques différentes. Cependant, tous ont un point commun : ils sont basés sur les principes de la théorie évolutionnaire. Ils simulent l'évolution naturelle des structures individuelles afin de trouver une solution optimale. Dans chaque génération, une nouvelle approximation de

solution optimale se produit par des processus de sélection des individus selon leurs performances dans le domaine du problème. Les individus sélectionnés vont être reproduits en utilisant des opérateurs empruntés aux génétiques naturelles. Ces processus mènent à l'évolution de la population des individus les mieux adaptés à leur environnement (Pohlheim, 2005).

Ces méthodes reçoivent de plus en plus d'intérêt en raison de leurs capacités potentielles à résoudre des problèmes complexes. Sous le concept d'algorithmes évolutionnaires, on trouve plusieurs méthodes tels les algorithmes génétiques, la programmation évolutionnaire, les stratégies d'évolution et la programmation génétique. Les étapes communes de ces méthodes peuvent être résumées comme suit (Bäck, 1996) :

- une initialisation aléatoire d'une population d'individus (des points de l'espace de recherche).

- une coopération et une compétition parmi les individus de la population concernée selon les principes Darwinistes et génétiques de la survie du "meilleur" (sélection, croisement et mutation).

- un nombre d'itérations (générations) faisant évoluer la solution (l'individu) courante et finissant par atteindre la solution optimale.

Une caractéristique importante pour les algorithmes évolutionnaires est l'absence d'information sur le gradient pour élaborer les solutions. Cette propriété donne aux algorithmes évolutionnaires une flexibilité satisfaisante leur permettant d'être utilisés aisément dans une grande variété de problèmes tels les problèmes fortement non-linéaires, les problèmes non-continus, ... . De plus, les algorithmes évolutionnaires travaillent sur un ensemble de points (une population) et non pas sur un seul point ; cela augmente la probabilité de trouver la solution optimale. Comme ces algorithmes utilisent les principes stochastiques, ils ne demandent aucune structure particulière pour le problème à optimiser.

Grâce à leurs nombreux avantages, les algorithmes évolutionnaires sont appliqués avec beaucoup de succès dans le domaine industriel et l'ingénierie. De nombreux problèmes liés aux systèmes de puissance sont résolus par les algorithmes évolutionnaires telles les répartitions économiques, la prévision de charges, la planification de génération, la coordination des contrôleurs, les études de sûreté des systèmes de puissance,... .

Les algorithmes génétiques, forment une des principales classes des algorithmes évolutionnaires ; ils ont suscité beaucoup d'enthousiasme depuis plusieurs années. Leur efficacité pour produire des solutions de qualité dans un grand nombre de problème d'optimisation est maintenant bien établie. Ils représentent les méthodes d'optimisations les plus utilisées.

Comme nous l'avons déjà indiqué, les algorithmes génétiques sont des méthodes de recherche stochastiques de solutions basées sur des mécanismes s'inspirant de processus naturels (sélection) et des phénomènes génétiques (croisement et mutation). Les travaux de scientifiques du XIX^e siècle (Lamarck, Darwin, Mendel,...) et du XX^e siècle (Watson et Crick) ont permis de mettre en évidence les principaux mécanismes à l'oeuvre au cours de l'évolution des populations. Ces recherches ont débouché sur l'idée que l'évolution repose

d'une part sur l'intervention du hasard au cours des croisements et des mutations, et d'autre part, sur un processus de sélection des individus les plus aptes à survivre dans un environnement donné. C'est précisément cette notion de hasard guidé par la sélection qui est à la base des algorithmes génétiques.

Dans les années soixante et soixante-dix, le professeur J. Holland à l'université de Michigan (Holland, 1975) a développé, sur la base des travaux précédents, les principes fondamentaux des algorithmes génétiques, son objectif étant de concevoir des systèmes artificiels possédant des propriétés similaires aux systèmes naturels. L'ouvrage de Goldberg (Goldberg, 1989) a permis de mieux faire connaître les algorithmes génétiques et il a marqué le début de l'intérêt actuel pour ces techniques.

La théorie des algorithmes génétiques utilise un vocabulaire similaire à celui de la génétique naturelle. Cependant, les processus naturels auxquels elle fait référence sont beaucoup plus complexes que les algorithmes génétiques.

On définit ainsi un individu dans une population. L'individu est représenté par un ou plusieurs chromosomes constitués de gènes qui contiennent les caractères héréditaires de l'individu. Les principes de sélection, de croisement, de mutation utilisés s'appuient sur les processus naturels du même nom (Barnier et al., 1999).

Pour un problème d'optimisation donné, un individu représente un point de l'espace de recherche c.-à-d. une solution potentielle. On lui associe la valeur du critère à optimiser qui définit sa performance. Pour progresser d'une population d'individus à une nouvelle population, on utilise séquentiellement les processus de sélection, de croisement et de mutation. La sélection a pour but de favoriser les meilleurs éléments de la population pour le critère considéré. Le croisement et la mutation ont pour but d'assurer l'exploration et l'exploitation de l'espace de recherche. Par conséquent, les individus les moins adaptés vont être exclus et les meilleurs vont survire pour construire la nouvelle population. Chaque itération de l'algorithme génétique représente une génération. Au fur et à mesure de la progression d'une génération à l'autre, la solution trouvée va converger vers la solution optimale à atteindre (Negnevitsky, 2002).

Généralement, nous pouvons dire qu'un algorithme génétique dans sa forme générale nécessite de préciser les points suivants :

- la fonction de performance pour calculer l'adaptation de chaque individu de la population.

- le croisement des individus d'une population pour obtenir la population de la génération suivante.

- l'opération de mutation des individus d'une population afin d'éviter une convergence prématurée.

- les paramètres de réglage : taille de la population, probabilités de croisement et de mutation, critère d'arrêt.

Ces points vont être discutés en détail dans la suite de ce chapitre, mais nous allons tout d'abord définir les expressions utilisées dans la théorie des algorithmes génétiques.

Dans un problème d'optimisation à n variables, nous faisons correspondre un gène à chaque variable cherchée. Chaque gène est représenté par une chaîne de caractères choisis dans un alphabet fini (souvent binaire). Les gènes s'enchaînent ensemble "bout à bout" pour

construire un chromosome, chaque chromosome représentant une solution potentielle sous une forme codée. Ces chromosomes constituent les briques de base contenant les caractéristiques héréditaires des individus. Un chromosome (ou plusieurs) forme un individu qui représente à son tour une solution potentielle dans l'espace de recherche correspondant du problème. Etant donné que les AGs travaillent sur un ensemble de points de l'espace de recherche, nous appelons l'ensemble des points choisis (à savoir les individus) une population. Au fur et à mesure des générations (itérations), une population des individus mieux adaptés va être créée.

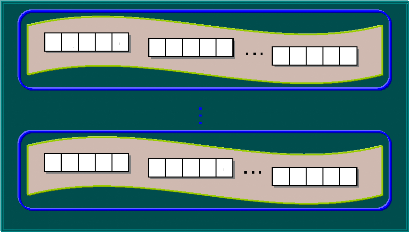
La figure (40) représente les relations entre les expressions génétiques d'un AG en codage binaire.

Figure 40. Les niveaux d'organisation des éléments d'un AG. 3.2.2- Codage et initialisation.

La première étape de la construction d'un AG est le choix du type de codage des paramètres du problème. La façon de coder les solutions potentielles est un facteur déterminant dans le succès d'un AG. Ainsi, plusieurs types de codage sont possibles dans la littérature, tels les codages binaires, Gray, réel,... . Le codage le plus populaire dans la représentation d'un AG est le codage binaire {0, 1 } ; les solutions sont codées selon des chaînes de bits de longueur fixe (Chipperfield et al., 1994). La plupart des théories liées aux AGs étaient élaborées en se basant sur le concept de codage binaire proposé par J. Holland et son groupe (Holland, 1975). Les opérateurs de l'AG, croisement et mutation, sont en effet plus faciles à mettre en oeuvre avec ce type de codage. En outre, le codage binaire représente la méthode la plus facile et la mieux adaptée de coder des éléments qu'ils soient réels, entiers, booléens, ... (Mitchell, 1996). On parle dans ce cas de génotype en ce qui concerne la représentation binaire d'un individu et de phénotype pour ce qui est de sa valeur réelle correspondante dans l'espace de recherche.

Une fois le choix du type de codage déterminé, une population initiale doit être créée pour le départ de l'AG. La population initiale a pour but de donner naissance à des générations successives, mutées et hybridées à partir de leurs parents. Le choix de la population initiale influence fortement la rapidité et l'efficacité de l'AG. Si la position de l'optimum dans l'espace de recherche est totalement inconnue, il est naturel de générer aléatoirement des individus en faisant des tirages uniformes dans chacun des domaines associés aux composantes de l'espace de recherche, en veillant évidemment à ce que les individus produits respectent les contraintes. Si par contre, des informations à priori sur le problème sont disponibles, il parait naturel de générer les individus dans un sous-domaine particulier afin d'accélérer la convergence. Habituellement, cette population initiale est générée d'une manière aléatoire et directement dans sa représentation codée.

Par exemple pour créer une population binaire de_Nind individus dans lesquels chaque chromosome (individu) est représenté par _Ngen gènes, il suffit simplement d'effectuer Nind × Ngen tirages de nombres aléatoires distribués uniformément sur l'ensemble {0, 1 }, (Chipperfield et al., 1994).

La seconde étape dans la construction de l'AG est le calcul de la performance (fitness) de chaque individu faisant partie de la population. Pour ce faire nous devons en premier lieu décoder les chromosomes (précisément les gènes de chaque chromosome) en les convertissant en leurs valeurs réelles (numériques) (Negnevitsky, 2002).

Considérons un problème d'optimisation de n variables à optimiser, où l'espace de recherche de chaque variable xj se trouve entre une limite inférieure _xmin,j et une limite supérieure xmax,j : D = [xmin, j , x _max,j] avec j = 1, 2,..., n. On associe des points du domaine D à

Sj chaînes de bits (Sj gènes) de longueur lS. Ainsi, chaque chaîne Sj sera donc composée de lS
éléments binaires : Sj = (si)j ; i = 1, 2,..., lS, où s_i ? {0,1}. Toute chaîne binaire Sj peut être

décodée en une valeur réelle xj en utilisant les deux règles suivantes (Negnevitsky, 2002) :

- dans la première, nous convertissons les valeurs binaires de chaque gène, en valeurs de base décimale selon la règle suivante :

- ensuite, nous calculons les valeurs réelles correspondantes appartenant à l'espace de recherche donné, par la règle suivante :

Par exemple, supposons que nous cherchons à maximiser une fonction f en fonction d'une variable réelle x appartenant à l'espace de recherche D = [-1 , 2]. Soit S une chaîne binaire représentant une solution possible avec une longueur lS = 22 :

En appliquant les relations (117) et (118), nous obtenons respectivement la valeur entière de x (en base décimale) et sa valeur réelle :

Après avoir générer la population initiale, nous devons attribuer à chacun des individus une note qui correspond à son adaptation au problème. Cette adaptation est la mesure de la fonction de performance associée à la fonction objectif du problème. Les notions de ces deux fonctions font l'objet du paragraphe suivant.

A l'inverse des méthodes déterministes d'optimisation, les algorithmes génétiques ne requièrent pas d'hypothèse particulière sur la régularité de la fonction à optimiser (objectif). Ainsi, les algorithmes génétiques n'utilisent pas les dérivées successives de la fonction objectif, ce qui rend leurs domaines d'application très vaste. Aucune hypothèse sur la continuité n'est également requise. Le peu d'hypothèses requises permet de traiter des problèmes très complexes. La fonction objectif peut être le résultat d'une simulation ou d'un modèle mathématique.

Généralement, la fonction objectif, d'un problème quelconque d'optimisation à K contraintes (dit problème contraint), peut être formulée comme suit :

Dk : l'espace des solutions réalisables (c.-à-d. l'ensemble des solutions potentielles en respectant les contraintes).

La fonction objectif peut être formulée d'un ensemble de fonctions de dimension n. Elle est donnée d'une façon générale comme suit : Fobj(X) = {f1 ,f2,L, f _i ,L, f_n }.

Lorsque i = 1 la fonction est dite monoobjectif, autrement elle est multiobjectif.

Contrairement à l'optimisation monoobjectif, la solution d'un problème d'optimisation multiobjectif est rarement unique. Elle est constituée de différentes solutions, représentant l'ensemble des meilleurs compromis vis-à-vis des différents objectifs du problème.

Les méthodes existantes pour formuler une fonction multiobjectif sont diverses. Nous allons expliquer brièvement ces méthodes qui peuvent être classées en trois grandes familles (Régnier, 2003) :

Chaque chromosome apporte une solution potentielle au problème à optimiser. Néanmoins, ces solutions n'ont pas toutes le même degré de pertinence. C'est à la fonction de performance (fitness) de mesurer cette efficacité pour permettre à l'AG de faire évoluer la population dans un sens bénéfique en cherchant la solution meilleure. Autrement dit, la fonction de performance, fp(X), doit pouvoir attribuer à chaque individu un indicateur représentant sa pertinence pour le problème que nous cherchons à résoudre. La performance sera donc donnée par une fonction à valeurs positives réelles. La construction d'une fonction de performance appropriée est très importante pour obtenir un bon fonctionnement de l'AG.

Dans le cas du codage binaire, la fonction de performance doit affecter une valeur positive au codage binaire correspondant (phénotype) à chaque chaîne binaire (génotype). Ainsi, elle permet de déterminer l'efficacité de la solution présentée par le génotype pour résoudre le problème.

La fonction de performance fp(X) est généralement dérivée de la fonction objectif Fobj(X) du problème. Elle est généralement donnée par la relation suivante :

Où : g : représente la transformation de la fonction objectif en performance relative.

Les AGs sont naturellement organisés pour résoudre les problèmes de maximisation (c. -à- d. trouver les valeurs positives maximales de la fonction objectif). Ainsi, pour les problèmes de maximisation, la fonction de performance peut être considérée comme la fonction objectif même. Le but de l'AG est alors simplement de trouver la chaîne binaire qui maximise la fonction de performance :

Dans le cas de problèmes de minimisation, le problème doit être modifié de sorte qu'il soit équivalent à celui de maximisation. Ainsi, il nous faudra modifier la fonction objectif de telle sorte que la fonction de performance soit maximale :

Une fois que la performance de chaque individu dans la population actuelle est évaluée, les mécanismes évolutionnaires entrent en jeu pour explorer et exploiter le plus largement possible l'espace de recherche et faire ainsi évoluer la population de manière progressive. Les opérateurs de l'AG cherchent à imiter ces mécanismes.

Pour déterminer les individus devant participer au résultat optimal de l'AG, un opérateur sélection doit être appliqué. Cet opérateur détermine la capacité de chaque individu à persister dans la population et à se reproduire. En règle générale, la probabilité de survie d'un individu sera directement reliée à sa performance relative au sein de la population. Cela traduit bien l'idée de la sélection naturelle Darwiniste : les gènes les plus performants ont la probabilité la plus élevée de se reproduire dans la population, tandis que ceux qui ont une performance relative plus faible auront tendance à disparaître. Néanmoins, cette approche doit être appréhendée avec précaution, puisqu'on souhaite transférer aux générations suivantes les meilleures caractéristiques génétiques et pas seulement les meilleurs individus.

En effet, un individu peut avoir certains gènes présents dans la solution optimale tout en présentant une performance médiocre : son élimination serait donc nuisible. Cependant, les individus ayant une bonne performance sont toujours plus susceptibles de posséder les bons gènes. Ainsi, une caractéristique importante d'un opérateur de sélection peut être définie en termes de pression sélective exercée sur la population. Cette notion doit être prise en compte d'une manière équilibrée. Si la pression sélective est trop forte, cela revient à "écraser" toute forme de diversité possible et la convergence de l'algorithme risque d'être prématurée en conduisant vers un optimum local. Si l'on passe à l'autre extrême, une pression sélective trop faible, l'algorithme tend à se rapprocher d'une simple recherche aléatoire avec une progression lente de la population (Duvigneau, 2006).

Il existe plusieurs méthodes pour représenter la sélection. La méthode la plus couramment utilisée proposée par Goldberg (Goldberg, 1989) est connue sous le nom de sélection par roulette biaisée (Roulette Wheel). D'autres méthodes de sélection sont aussi apparues dans la littérature, la plus connue étant celle du tournoi (Tournament Selection).

Dans cette méthode, chaque chromosome est copié dans la nouvelle population avec une probabilité proportionnelle à sa performance relative : on parle ainsi de sélection proportionnelle à la performance. Dans un codage binaire, le principe de cette méthode consiste à associer à chaque individu Xi (d'une population de taille _Nind) une probabilité Rp,i proportionnelle à sa performance fp(Xi). Cette probabilité (dite la fonction de performance

normalisée) peut être ainsi calculée comme le taux de la performance du i^ème individu pondéré par la somme des performances de toute la population :

On doit donc effectuer autant de tirages aléatoires qu'il y a d'individus dans la population. Chaque individu est alors reproduit avec la probabilité R_p ; certains individus (notés les bons) auront plus de chance d'être reproduits, les autres (notés mauvais) seront éliminés.

Dans la pratique, nous associons à chaque individu un secteur (ou un segment) dont la surface (la longueur) est proportionnelle à sa performance. Ces éléments sont ensuite concaténés sur une base normalisée entre 0 et 1. Enfin, nous reproduisons le principe de tirage aléatoire utilisé dans les roulettes de casinos, d'où le nom de ce mécanisme de sélection, avec une caractéristique linéaire (sélection proportionnelle à la performance). Nous tirons alors un nombre aléatoire, de distribution uniforme entre 0 et 1, et nous déterminons l'individu sélectionné. Ainsi, les grands secteurs (c.-à-d. les bons individus) auront plus de chance d'être choisis que les petits secteurs. Les individus ayant une forte performance sont donc privilégiés au détriment des individus moins forts, tout en gardant la notion de tirage aléatoire. Ainsi, avec cette méthode un même individu pourra être sélectionné plusieurs fois. Mais une certaine diversité est cependant maintenue, car même les individus les moins performants conservent une chance d'être choisis. Pour garder la même taille de la population initiale dans la population suivante, on doit lancer la roulette autant de fois qu'il y a d'individus de la population.

Considérons un problème simple de maximisation dont la fonction objectif est donnée par la forme suivante :

Nous traitons ce problème en décodant les points de l'espace de recherche en chaînes binaires de longueur lS = 8, et en initialisant une population de départ de 4 individus (Nind = 4).

Pour appliquer la méthode de la roulette biaisée, nous calculons en premier lieu, pour chaque individu, la fonction de performance fp(Xi) et la probabilité correspondante Rp,i.

N° individu	Chromosome Si					Valeurs décodées Xi (individus)	Performance fp(Xi) =Fobj = 4·x·(1-x)	Probabilité Rp,i = fp(Xi) / ?( fp(Xi))	Intervalles de probabilité
1	1	0 1	1 1	0 1	0	0.7294	0.7895	0.29	[0 , 0.29]
2	1	1 0	1 1	1 1	0	0.8706	0.4507	0.18	[0.29 ,	0.47]
3	0	0 0	1 1	0 1	0	0.1020	0.3665	0.15	[0.47 ,	0.62]
4	0	1 1	0 1	1 0	0	0.423 5	0.9766	0.38	[0.62	, 1]
							? fp = 2.5831

Tableau 1. Résultats de l'évaluation des individus dans la population initiale.

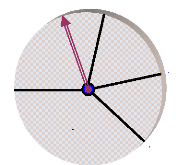
Ensuite, nous associons à chaque intervalle de probabilité un secteur équivalent de la roulette (c.-à-d. un individu), comme le montre la figure (41) :

Enfin, nous effectuons le tirage d'un nombre aléatoire dans l'intervalle [0,1] et nous reproduisons ce tirage 4 fois. Nous sélectionnons ainsi les individus en positionnant chaque nombre obtenu par tirage dans le secteur équivalent de la roulette. Le tableau (2) donne la valeur obtenue pour chaque tirage et les individus sélectionnés correspondants.

N° tirage	Valeur obtenue	Individus sélectionnés		Chromosomes équivalents
1	0.43	X2	X_á 1	=	1	1 0	1 1	1 1	0
2	0.89	X4	X_á 2	=	0	1 1	0 1	1 0	0
3	0.18	X1	X_á 3	=	1	0 1	1 1	0 1	0
4	0.75	X4	X_á 4	=	0	1 1	0 1	1 0	0

Nous trouvons que l'individu X3 est éliminé de la population tandis que l'individu X4 est reproduit deux fois.

La méthode de la roulette, comme les autres méthodes de sélection proportionnelle à la performance, exige principalement deux étapes pour créer la population intermédiaire. Premièrement, nous calculons la performance moyenne de la population, ensuite nous calculons la probabilité de sélection pour chaque individu. La méthode du tournoi est plus directe, puisqu'elle ne demande pas le calcul de la performance moyenne de la population (Mitchell, 1996).

Cette méthode consiste à simuler _Nind tournois, un individu étant sélectionné à chaque fois. Un échantillon de n_p individus (2 minimum) est prélevé au hasard à chaque tournoi. Le

participant dans l'échantillon ayant la performance la plus élevée sera alors adopté pour accéder à la population intermédiaire. Etant donné que le choix des échantillons des individus se fait aléatoirement, il est donc tout à fait possible que certains individus participent à plusieurs tournois. Il est aussi possible qu'un de ces individus gagne plusieurs fois et il sera par conséquent copié autant de fois dans la population intermédiaire. La pression sélective de cette méthode est directement reliée à la taille de l'échantillon (n_p). Plus la taille n_p est grande, plus la pression est grande (Duvigneau, 2006). Cette méthode est caractérisée par une pression sélective plus forte que celle de la méthode de la roulette biaisée : pour qu'un individu peu performant puisse être sélectionné, il faut que tous ses adversaires soient moins bons que lui. Ainsi, cette méthode doit être privilégiée dans le cas d'une population de grande taille.

Dans le cas où le nombre de participants dans chaque tournoi est égal à deux (n_p = 2), la sélection est dite par « tournoi binaire ». La sélection d'un individu _Xsélect,K par tournoi binaire peut être faite de la façon suivante :

i, j sont des nombres aléatoires non-égaux, i, j ? {1,2,L, Nin d }. 3.2.4.3- Conclusion.

La méthode de la roulette reste la méthode de sélection la plus utilisée car elle est relativement efficace. Cependant, pour certains problèmes, elle est "un peu trop aléatoire". C'est pour cela que pour certains problèmes, la méthode du tournoi est plus préférée. Cette dernière étant "moins aléatoire" que la roulette, elle permet ainsi une plus grande fiabilité.

Disposant finalement d'une population d'individus non-homogène, la diversité de la population doit être entretenue au cours des générations afin de parcourir le plus largement possible l'espace de recherche. Pour ce faire, les individus sélectionnés (dits les parents) sont alors introduits dans le bassin de reproduction (Mating Pool) où ils seront de nouveaux choisis aléatoirement pour voir leurs chromosomes subir des transformations par les opérateurs génétiques. Ces derniers sont les opérateurs de croisement et de mutation (dits les opérateurs de diversification et d'intensification du milieu).

Dans les AGs, le croisement est considéré comme le principal opérateur pour produire des nouveaux chromosomes. Comme son homologue dans la nature, le croisement produit de nouveaux individus en leur transférant quelques parties de la matière génétique de leurs parents. L'objectif du croisement est donc d'enrichir la diversité de la population en manipulant la structure des chromosomes (Chipperfield et al., 1994). Initialement, le croisement associé au codage par chaînes de bits (codage binaire) est le croisement à découpage de chromosomes.

Ainsi, dans le codage binaire, les individus, qui résultent de la sélection, sont groupés de manière aléatoire par paire définissant ainsi les parents. Ensuite, chaque couple peut subir un croisement avec une probabilité P_c donnée. Cette étape peut être effectuée comme suit

Pour chaque couple, un nombre aléatoire P est tiré dans l'intervalle [0,1] et comparé ensuite avec la probabilité de croisement P_c :

- si P > P_c, le couple ne subit pas de croissement et un clonage de chromosome aura

- si P < P_c, le croisement a lieu et un échange des parties des chromosomes des parents

Après avoir tiré les couples qui vont être "croisés", l'opérateur de croisement peut donc être appliqué. Plusieurs types de croisement sont présentés dans la littérature, tels : le croisement seul point, le croisement multipoints, le croisement uniforme,... .

Dans ce type de croisement, un point de croisement est choisi aléatoirement pour le couple ; la position de ce point M est définie par:

Les deux parents seront ainsi divisés en deux segments ; tête et queue. Le segment tête du premier parent est combiné avec le segment queue du deuxième parent : on obtient ainsi le premier enfant. La combinaison entre le segment tête de deuxième parent et le segment queue de premier parent produit le deuxième enfant.

Pour mieux expliciter ce type de croisement, nous allons l'appliquer à l'exemple présenté dans le paragraphe de la sélection.

Considérons la population de quatre individus déterminée par l'opération de sélection, nous pouvons la diviser aléatoirement en deux couples qui peuvent être par exemple : [(X_á1, Xá4), (Xá2, X_á3)].

Considérons ensuite une probabilité de croisement P_c = 50% (nous avons choisi une faible probabilité de croisement étant donné la "petite" taille de la population considérée). Cela signifie que nous pouvons tirer seulement un seul couple au hasard et lui appliquer le croisement chromosomique. Supposons que le hasard ait désigné le deuxième couple (Xá2, Xá3) pour croisement, il nous faut maintenant déterminer la position du point M de croisement dans les parents. Cette position peut être tirée au hasard ou choisie préalablement. 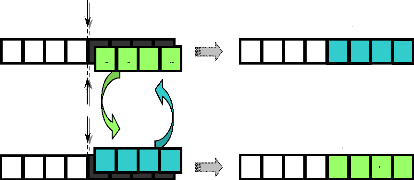Afin de rendre l'exemple plus parlant, nous décidons d'appliquer ce croisement sur le milieu (M = 4) du chromosome, comme le montre la figure (42).

Ainsi, l'application de l'opération de croisement engendre deux nouveaux individus (les deux enfants Xâ₂ et Xâ 3).

Le croisement en un seul point a l'avantage d'être simple et facile à appliquer. De plus, ce type de croisement donne de bons résultats dans des applications où certaines informations importantes sur le problème sont déjà connues. Enfin, pour des problèmes d'optimisation en temps réel ou des problèmes ayant un grand nombre de variables, cette méthode peut donner une convergence rapide vers une solution optimale.

A la différence du croisement seul point, ce type de croisement s'applique en plusieurs points (m points) et chaque chromosome sera ainsi découpé en (m+ 1) segments. La position de chaque point, Mi, se détermine aléatoirement, avec :

m : le nombre de points de croisement donné (Pour m = 1, on retourne au cas du croisement seul point).

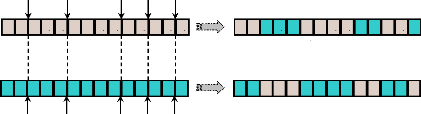
Ensuite, les bits entre deux points de croisement successifs du premier parent vont être échangés avec les bits correspondants du deuxième parent. La figure (43) montre un croisement en cinq points (m = 5), les points de croisement Mi étant {2, 5, 9, 11, 13 } :

La nature complexe du croisement multipoints permet d'obtenir une bonne exploration de l'espace de recherche au détriment d'une convergence rapide vers la bonne solution comme le ferait la première méthode. Ainsi, cette méthode de croisement est beaucoup plus robuste.

Dans le croisement multipoints, chaque segment du chromosome, compris entre deux points de croisement successifs, peut contenir un ou plusieurs bits. Le croisement uniforme généralise ce schéma pour lier à chaque bit un point de croisement. Pour ce faire, un chromosome masque, de même longueur que le chromosome des parents, est créé : la valeur de ses bits étant aléatoire. La parité de chaque bit dans le masque détermine successivement le parent qui va donner ses bits à l'enfant (Chipperfield et al., 1994). L'enfant généré va copier le bit de son premier parent si le bit correspondant de masque est `1', ou de son deuxième parent si le bit correspondant de masque est `0'. Ce schéma ne fait générer qu'un seul enfant. Pour générer le deuxième, un autre chromosome masque est nécessaire. Les bits de ce dernier sont créés par complémentation des bits du premier masque. L'explication de cette méthode est décrite par l'exemple suivant :

La nature complexe du croisement uniforme, comme pour le croisement multipoints, améliore encore l'exploration de l'espace de recherche. Avec le croisement uniforme, basé sur le transfert de matière génétique d'un parent à un enfant par bit de chromosome, on obtient un algorithme génétique beaucoup moins dépendant du schéma de codage. Enfin, cette méthode peut être plus précise dans l'identification d'optima globaux.

A la suite des opérateurs de sélection et de croisement, on mime à nouveau un phénomène biologique, celui de la mutation. Au niveau biologique, une mutation est une modification de l'information génétique par dégradation ou substitution locale de paire de base : ceci permet de produire une nouvelle structure génétique. L'opérateur de mutation dans le cas des AGs possède la propriété d'ergodicité du parcours de l'espace de recherche : cette propriété indique que l'AG sera susceptible d'atteindre tous les points de l'espace, sans pour autant les

parcourir tous dans le processus de résolution (Bontemps, 1995). La séquence des opérations de sélection et de croisement peut mener l'AG à "stagner" dans un ensemble de solutions identiques. Dans de telles conditions, tous les chromosomes deviennent identiques et, ainsi, la performance moyenne de la population ne s'améliore plus. Dans ce cas, la mutation aide l'AG à éviter la perte de diversité génétique et, par conséquent, elle garantit que l'AG ne va pas être bloqué dans un optimum local (Negnevitsky, 2002).

Le principe de la mutation consiste à modifier, avec une probabilité P_m faible, certains bits des chromosomes. Nous tirons tout d'abord pour chaque bit un nombre aléatoire P dans l'intervalle [0,1]. Puis, nous le comparons avec une probabilité de mutation P_m donnée :

Ainsi, le bit choisi pour muter sera remplacé par une valeur aléatoire, souvent proche de la valeur initiale. Dans le cas du codage binaire, cette mutation s'effectue simplement en remplaçant le bit `0' par `1' et vice versa.

Pour continuer la présentation de l'opérateur de mutation, nous reprenons l'exemple précédent (paragraphe croisement) et nous appliquons la mutation sur la population résultante du croisement.

Nous proposons arbitrairement une probabilité de mutation P_m = 0.01. Pour déterminer les bits qui subiront une mutation, nous tirons un nombre aléatoire compris entre 0 et 1 pour chaque bit et nous le comparons avec P_m. La figure suivante montre les bits choisis pour la mutation et l'application de cet opérateur :

Les individus résultants de la mutation, (Xã1, Xã2, Xã3, Xã4), vont former la nouvelle population qui va remplacer la population initiale pour la deuxième génération.

Pour réaliser une boucle d'une itération de l'AG, ce dernier doit d'abord regrouper les individus survivants après mutation dans une nouvelle population. Ensuite, l'AG va calculer la performance pour chaque nouvel individu. Enfin, si un critère d'arrêt de l'algorithme n'est pas encore atteint, la nouvelle population doit alors remplacer la population actuelle et une nouvelle boucle sera ainsi lancée.

Puisque les AGs sont des méthodes de recherches stochastiques, il est difficile de spécifier de façon rigoureuse des critères de convergence. Par exemple, la performance d'une population peut rester stable pour un certain nombre de générations avant qu'un individu supérieur puisse apparaître. Ainsi, l'application d'un critère d'arrêt devient une vraie problématique. Une pratique commune est d'arrêter l'AG après certain nombre de générations et d'examiner ensuite la qualité de la solution trouvée par rapport à la définition du problème. Un nombre typique de générations peut aller de 50 jusqu'à 500 générations (Negnevitsky, 2002).

Par ailleurs, d'autres critères peuvent être appliqués pour déterminer l'arrêt de l'AG tels que :

Nous terminons l'exemple que nous avons commencé de traiter par le calcul de la performance de chaque nouvel individu :

N° individu	Chromosome Sãi						Valeurs décodées Xãi	Performance fp(Xãi) =Fobj
1	0	1 1	1	1 1	1	0	0.4941	0.9999
2	0	0 1	0	1 1	1	0	0.1804	0.5914
3	1	0 1	1	1 1	1	0	0.745 1	0.7597
4	0	1 1	0	1 1	0	0	0.4235	0.9766
								? fp = 3.3276

Tableau 3. Résultats de l'évaluation des individus dans la nouvelle population.

En comparant le tableau (1) de l'évaluation de la population initiale et le tableau (3) de

l'évaluation de la nouvelle population, nous pouvons tirer les remarques suivantes :

- le meilleur individu (Xãj) dans la nouvelle population est un individu nouveau (issu

- ce nouvel individu présente une performance supérieure à celle du meilleur individu de la population initiale (fp(Xãj) = 0.9999 contre fp(Xj) = 0.9766).

- l'individu X4 reste toujours présent dans la nouvelle population (renommé Xã4).

- la nouvelle performance totale (et donc la performance moyenne) est supérieures à la valeur de départ (? fp(Xãi) = 3.3276 contre ? fp(Xi) = 2.5831).

- l'individu (Xã1), associé à la performance maximale fp(Xã1), peut être ainsi considéré comme la solution optimale du problème.

Etant donné que le problème traité est très simple, l'AG a pu atteindre une solution optimale dés la première itération.

Généralement, la recherche d'une solution optimale dans un espace complexe implique souvent un compromis entre deux objectifs apparent contradictoires : l'exploration et l'exploitation.

L'exploration a pour objectif une recherche large des régions nouvelles et inconnues de l'espace de recherche en récoltant de l'information sur le problème à optimiser. L'exploitation se propose d'utiliser l'information acquise aux points déjà explorés pour définir et parcourir ainsi les zones les plus intéressantes de l'espace de recherche. Une recherche purement aléatoire (comme le fait la méthode de Monte-Carlo) est bonne pour l'exploration mais mauvaise pour l'exploitation alors que la recherche dans le voisinage (comme le fait la méthode de la descente) est une bonne méthode d'exploitation mais une mauvaise méthode d'exploration. La littérature montre que les algorithmes génétiques peuvent réaliser un compromis équilibré et raisonnable entre exploration et exploitation. Mais il est important de bien doser l'usage de ces deux ingrédients afin que l'exploration puisse identifier rapidement des régions de l'espace de recherche qui contiennent des solutions de bonnes qualités, sans perdre trop de temps à exploiter des régions moins prometteuses. Pour ce faire, il faut ainsi ajuster les paramètres de réglage des opérateurs génétiques, sachant que le croisement favorise plus l'exploration tandis que la mutation favorise plus l'exploitation.

Il y a principalement trois paramètres de base pour le "fonctionnement" d'un AG : - le nombre d'individus dans la population _Nind (dit la taille de la population).

La réussite et la rapidité d'un AG dépendent fortement des valeurs choisies pour ces paramètres. Le bon réglage de ces paramètres est un problème parfois délicat (Mitchell, 1996).

Nous discutons ci-dessous l'influence de chaque paramètre et la gamme de valeurs qu'il peut prendre :

Ce paramètre doit être judicieusement réglé en fonction de la taille du problème. Généralement, nous pouvons dire que si la taille de la population est :

- trop faible, l'AG peut converger trop rapidement vers de mauvaises solutions. - trop grande, le temps de calcul de l'AG peut s'avérer très important.

En règle générale, plus la taille de la population est grande, plus le nombre de solutions potentielles évaluées est élevé. La littérature montre que les meilleures valeurs de taille de population sont comprises entre 50 et 100 individus (Mitchell, 1996).

La mutation, comme nous l'avons vu, est un opérateur secondaire, mais elle reste très importante pour l'AG. Elle a pour objectifs l'introduction de diversité dans la population et la meilleure exploitation de l'espace de recherche. Ainsi, si la probabilité de mutation est :

Le taux habituel de la probabilité de mutation est choisi entre 0.001 et 0.05. 3.3- Conclusion.

Les algorithmes génétiques sont des méthodes métaheuristiques d'optimisation globale basées sur des concepts de génétique et de sélection naturelle. Le composant principal des AGs est le gène qui se compose d'une chaîne de caractères (souvent binaire). Les gènes s'enchaînent et forment les chromosomes. Ces derniers forment les individus dans l'espace de recherche. Ainsi, les AGs travaillent sur une population d'individus, où chacun de ces derniers représente une solution possible pour le problème donné. Dans chaque itération de l'AG, la performance de chaque individu de la population courante est calculée. Les opérateurs de génétiques, sélection, croisement et mutation, sont appliqués successivement pour créer une nouvelle population jusqu'à l'approche rigoureuse de la solution optimale.

- Ils ne demandent pas d'informations à priori ou des propriétés particulières de la fonction objectif du problème.

- Leurs performances par rapport aux algorithmes classiques sont bien remarquées lorsque par exemple les espaces de recherches sont importants.

- Outre leur facilité de programmation et de manipulation, ils sont facilement adaptables à tout type de problème d'optimisation.

- Ils peuvent être utilisés avec profit pour traiter des problèmes n'étant pas optimisables efficacement par des approches purement mathématiquement.

- Le temps de calcul est souvent important : ils nécessitent de nombreux calculs, en particulier au niveau de la fonction objectif.

- Les paramètres de réglage (telles la taille de la population, la probabilité de croisement, ...) sont parfois difficiles à déterminer. Or le succès de l'évolution en dépend et plusieurs essais sont donc nécessaires.

- Ils ne garantissent pas toujours la découverte de l'optimum global en un temps fini. En effet, lorsqu'une population évolue, il se peut que certains individus occupant à un instant une place importante au sein de cette population deviennent majoritaires. A ce moment, il se peut que la population converge vers cet individu en s'écartant ainsi d'individus plus intéressants et en s'éloignant de l'individu vers lequel on devrait converger.

Nous pouvons conclure que l'efficacité des AGs dépend d'un compromis entre deux objectifs contradictoires : la rapidité et la précision. La rapidité est souvent mesurée en nombre d'évaluations de la fonction objectif. Cette dernière représente la plupart du temps la partie la plus "gourmande" en temps de calcul. La précision se rapporte à la distance entre l'optimum trouvé par l'AG et l'optimum réel, du point de vue de la solution ou de la valeur. Bien souvent, un AG rapide est peu précis, et inversement.

Dans le chapitre suivant, nous utilisons les principales caractéristiques des AGs développés dans ce chapitre pour une optimisation globale des PSSs.

Etude de la stabilité aux petites perturbations dans les grands réseaux électriques: Optimisation de la régulation par une méthode metaheuristique

Chapitre III