Chapitre II
Stabilité du système
de
puissance
2.1- Introduction.
La bonne performance d'un système de puissance
dépend de sa capacité de fournir à tout moment la
puissance demandée dans des conditions de qualité satisfaisantes,
en maintenant les niveaux de tension et de fréquence dans des limites
acceptables.
La stabilité est considérée l'une des
trois grandes études des systèmes de puissance, les deux autres
étant l'écoulement de puissance et l'analyse de défauts.
Il est clair que les études de stabilité sont les plus complexes,
tant en termes de modélisation que de méthodes de recherche des
solutions.
La stabilité d'un système de puissance est la
capacité du système, pour des conditions initiales
données, de retrouver un point d'équilibre suite à une
perturbation. Ainsi, la stabilité est une condition d'équilibre
entre des "forces" opposées et l'instabilité résulte d'une
perturbation menant à un déséquilibre important entre les
"forces" opposées.
Cette instabilité peut avoir différentes formes
et peut être influencée par différents facteurs. L'analyse
des problèmes de stabilité implique l'indentification des
facteurs essentiels contribuant à l'instabilité et le
développement de méthodes pouvant améliorer la
stabilité du système.
Le problème de la stabilité des systèmes
dynamiques a été et reste le sujet de préoccupation majeur
du travail des mathématiciens, des physiciens et des ingénieurs
(Hahn, 1967; Parks et al., 1981).
Les critères d'analyse de stabilité peuvent
être classés en deux grandes catégories :
- Les critères fréquentiels : tels les
critères de Nyquist, le diagramme de Bode, ... . Ces critères
dépendent de la fonction de transfert du système.
- Les critères temporels : tels les critères de
Kalman, les méthodes de Lyapunov, ... . Ces critères
dépendent du modèle d'état du système.
Une contribution majeure aux études de stabilité
fut apportée par A.M. Lyapunov en 1892, dont les travaux ont
été connus dans les années soixante. Il a introduit la
majorité des concepts et définitions de base concernant la
stabilité des systèmes représentés par des
systèmes différentiels arbitraires mais a aussi fourni les
principaux résultats théoriques.
La stabilité au sens de Lyapunov est une théorie
générale valable pour tout système décrit par des
équations différentielles linéaires ou
non-linéaires.
Ce chapitre traite de la stabilité du système de
puissance. Il est divisé en trois grandes parties. La première
partie rappelle les principes de la stabilité au sens de Lyapunov. Dans
la deuxième partie, nous rappelons les caractéristiques des
différents types de stabilité d'un système de puissance.
La troisième partie s'intéresse plus particulièrement
à la stabilité angulaire aux petites perturbations avec les
stabilisateurs de puissance (PSSs).
2.2- La stabilité au sens de Lyapunov. 2.2.1-
Définitions de la stabilité.
Considérons un système non-autonome
(dépendant du temps) et non-commandé (entrée nulle)
décrit par l'équation différentielle non-linéaire
:
x&(t) =
f(x(t),t) (83)
Où : x est un vecteur d'état et
x& sa dérivée dans le temps t.
Ce système est dit en équilibre autour d'un point
xe si, en l'absence d'influence externe, son état ne
varie pas au cours du temps :
f(xe,t) = 0 (84)
Ainsi, nous nous intéressons aux comportements des
trajectoires du système au voisinage de ses points
d'équilibre.
Nous rappelons dans ce qui suit quelques définitions
importantes qui forment l'approche de la stabilité au sens de
Lyapunov.
2.2.1.1- Stabilité du point
d'équilibre.
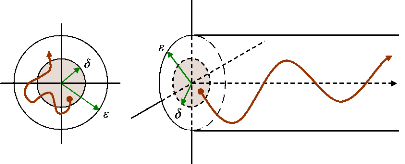
Un point d'équilibre xe est dit stable
si, pour tout å > 0, il existe une valeur
ä>0 tel que :




x(t0) - xe
<ä x(t) - xe
<å ?t = t0 (85)
Où, t0 est l'instant initial.
Dans le cas contraire, xe est dit
instable.


Ainsi, la stabilité au sens de Lyapunov signifie que la
trajectoire x(t), avec une condition initiale
x(t0), doit rester proche du point d'équilibre
xe (c.-à-d. x(t0) -
xe <ä), pour tout t = t0. Pour
cela, les solutions x(t) doivent rester à
l'intérieur de la région délimitée par
x(t) - xe < å ,
c.-à-d. rester dans un "tube" de rayon å autour de la trajectoire
x(t) = xe, figure (19), ( Fouad et
al., 1991).
t
x(t)
t0
Figure 19. Stabilité d'un point
d'équilibre.
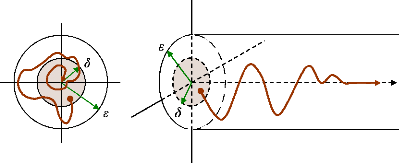
2.2.1.2- Stabilité asymptotique.
Un point d'équilibre est asymptotiquement stable s'il est
stable et si :
lim ( ) - =
t x t x
?8 e
0 (86)


La stabilité asymptotique signifie que non seulement le
point d'équilibre est stable, mais qu'on est aussi capable de
déterminer un domaine proche du point d'équilibre tel que
n'importe quelle trajectoire, issue d'un état initial
x(t0) appartenant à ce domaine, tende vers
xe quand t tend vers 8, figure (20), ( Fouad
et al., 1991).
t
x(t)
t0
Figure 20. Stabilité
asymptotique.
Un ensemble d'états initiaux x(t0)
à partir desquels les trajectoires convergent vers un point
d'équilibre asymptotiquement stable est appelé un domaine
d'attraction D.
La stabilité asymptotique est la
propriété généralement recherchée en
pratique. Il faut cependant remarquer que la définition ci-dessus ne
donne pas d'information sur la vitesse à laquelle la trajectoire
x(t) converge vers l'équilibre. C'est pourquoi, on
introduit la notion de stabilité exponentielle qui permet de
caractériser cette vitesse.
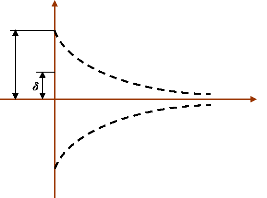
2.2.1.3- Stabilité exponentielle.
Un point d'équilibre est exponentiellement stable si pour
tout å > 0, il existe des constantes a>0,
b)>0 et ä>0 tel que :
x(t0) - xe
<ä ( ) - < · ( 0 ) - · ? t =
t0 (87)
bt
x t x e a x t x e e -





Cette stabilité signifie que le vecteur d'état,
pour une condition initiale x(t0), converge vers un point
d'équilibre xe plus rapidement qu'une fonction
exponentielle ; b est appelé le taux de convergence. Par
ailleurs, la stabilité exponentielle implique la stabilité
asymptotique qui implique elle-même la stabilité d'un point
d'équilibre. La figure (21) illustre schématiquement la
définition de la stabilité exponentielle (Miller et al.,
1982).
2.2.2- Méthodes d'analyse de stabilité au
sens de Lyapunov. 2.2.2.1- Première méthode de Lyapunov
(méthode indirecte).
La première méthode de Lyapunov se base sur
l'analyse du comportement du système linéarisé autour de
son point d'équilibre. Plus précisément, on examine les
valeurs propres ëi du système de la matrice Jacobienne (la
matrice d'état) A évaluée au point
d'équilibre xe :
Les caractéristiques de stabilité de cette
méthode ont été expliquées dans le premier chapitre
(§§-1.4.3.2). Nous les rappelons ci-dessous :
- si toutes les valeurs propres de la matrice d'état sont
à partie réelle strictement négative (?i,
Réel(ëi (A)) < 0), le
système est exponentiellement stable à son point
d'équilibre. Dans ce cas, on a e
lim ?8 ( ) .
t x t = x
- si la matrice d'état possède au moins une valeur
propre à partie réelle strictement
.
positive ( ? i,
Réel(ëi (A)) > 0), le
système est instable. Dans ce cas, on a = 8
lim ?8 x ( t )
t
La première méthode est simple à
appliquer mais étant donné que cette méthode repose sur
une linéarisation du système, sa validité est alors
limitée à un certain voisinage du point d'équilibre.
Lorsque la linéarisation du système n'est pas possible ou
lorsqu'on veut analyser le système sans le résoudre
explicitement, on utilise la deuxième méthode de Lyapunov
(Slotine et al., 1991).
-
t
a e - · -
·
b ( t t0 )
a
a e - · -
·
b ( t t0 )
t0
Figure 21. Stabilité exponentielle.
2.2.2.2- Deuxième méthode de Lyapunov
(méthode directe).
La deuxième méthode de Lyapunov s'appuie sur une
observation physique fondamentale :
Si l'énergie totale d'un système,
linéaire ou non-linéaire, est continûment dissipée
(on parle de système dissipatif), alors le système doit tendre
finalement vers un point d'équilibre.
Ainsi, l'idée de Lyapunov, pour étudier la
stabilité d'un système donné, est d'examiner la variation
d'une seule fonction scalaire (appelée la fonction de Lyapunov)
dépendant de l'énergie totale du système (Khalil, 1996).
Autrement dit, cette méthode est basée sur la définition
d'une fonction de Lyapunov décroissante le long des trajectoires du
système à l'intérieur du domaine d'attraction. Cette
méthode s'énonce comme suit (Custem, 2002, II) :
Le point d'équilibre xe est stable
s'il existe dans un certain voisinage ? de ce dernier une
fonction de Lyapunov V(x) telle que :
· V(xe)=0
· V(xe)>0 pour tout x
dans ?
· V(x)=0
d dans ?
dt
Les deux premières conditions expriment la
présence de surfaces fermées entourant le point
d'équilibre xe. La troisième condition
exprime que les trajectoires du système soit restent sur ces surfaces,
soit coupent les surfaces en entrant à l'intérieur d'elles,
d'où la stabilité du point d'équilibre.
La deuxième méthode de Lyapunov permet, outre
l'analyse de stabilité d'un point d'équilibre du système,
de déterminer une partie de son domaine d'attraction en ce sens que
? est inclus dans D.
2.2.3- Conclusion.
Dans cette partie, nous avons rappelé les
définitions de la stabilité au sens de Lyapunov. Nous avons
également présenté les méthodes d'analyse de la
stabilité d'un système linéaire (1ère
méthode de Lyapunov) et d'un système non-linéaire
(2ème méthode de Lyapunov).
Dans la partie suivante, nous allons exposer les
définitions et les principales caractéristiques des
différents types de la stabilité de système de
puissance.
2.3- Les différents types de la stabilité
de système de puissance.
Pendant des années, des recherches diverses et
complexes étaient effectuées pour comprendre les problèmes
de stabilité des systèmes de puissance. Ainsi de nombreuses
définitions de la stabilité de systèmes de puissance
étaient proposées en insistant sur les divers aspects qui
reflètent la manifestation de l'état stable de système. La
définition la plus récente, que nous adopterons, est le
résultat d'un groupe de travail conjoint IEEE/CIGRE (IEEE/CIGRE,
2004).
La stabilité d'un système de
puissance est la capacité d'un système
d'énergie électrique, pour une condition de fonctionnement
initiale donnée, de retrouver le même état ou un autre
état d'équilibre après avoir subi une perturbation
physique, en gardant la plupart des variables de système dans leurs
limites, de sorte que le système entier reste pratiquement
intact.
Ainsi un système de puissance possédant un
état d'équilibre est considéré comme stable, si
suite à une perturbation, le système peut encore retrouver une
position d'équilibre. Le système est également
considéré comme stable s'il tend vers une autre position
d'équilibre située dans la proximité du point
d'équilibre initial. Cela correspond aux propriétés de la
stabilité du point d'équilibre au sens de Lyapunov.
La stabilité d'un système de puissance
électrique représente la propriété du mouvement du
système autour d'un état d'équilibre (c.-à-d. les
conditions de fonctionnement initiale).
Dans un état d'équilibre, toutes les
différentes forces opposées sont égales :
- soit instantanément : c'est le cas des points
d'équilibre,
- soit périodiquement : c'est le cas des variations
périodiques lentes en raison des petites fluctuations continuelles sur
les charges ou la génération.
Ainsi, la stabilité d'un système de puissance
dépend non seulement des conditions de fonctionnement initiales elle
dépend également de la nature physique et de l'amplitude de la
perturbation.
En raison de la taille, de l'importance et de la
complexité des problèmes de stabilité, il est très
intéressant de faire des simplifications et des hypothèses
appropriées pour représenter analytiquement le système.
Pour analyser et résoudre les problèmes
d'instabilité dans les systèmes de puissance, il est
indispensable de regrouper les différents groupes de stabilité.
Cette classification de la stabilité est basée sur les
considérations suivantes (Kundur, 1994) :
- la nature physique de l'instabilité
résultante.
- l'amplitude de la perturbation.
- la plage de temps nécessaire pour assurer la
stabilité.
- les dispositifs et les processus nécessaires pour
assurer la stabilité.
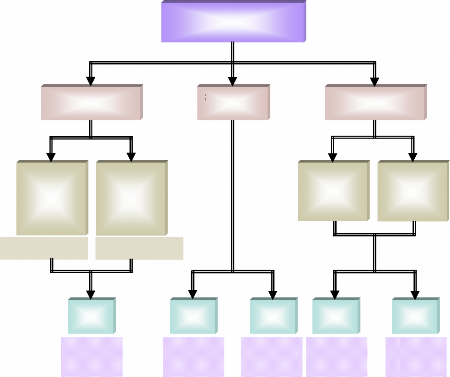
Habituellement, la stabilité est divisée en trois
groupes, à savoir : - la stabilité de l'angle de rotor.
- la stabilité de tension.
- la stabilité de fréquence.
La figure (22) présente ces principales catégories
de stabilité d'un système de puissance et leurs
sous-catégories.
Stabilité dynamique
perturbations
Stabilité de
l'angle de
rotor aux
petites
Stabilité de l'angle
de rotor
de l'ordre de
10 à 20
secondes
court
terme
rotor aux
grandes
perturbations
Stabilité transitoire
Stabilité de
l'angle de
STABILITE DE SYSTEME
DE PUISSANCE
de l'ordre
de plusieurs
secondes
terme
court
Stabilité de la
fréquence
de l'ordre
de plusieurs
minutes
long
terme
Stabilité de
la tension
aux petites
perturbat ions
de l'ordre
de plusieurs
secondes
court
terme
Stabilité de la
tension
la tension
aux grandes
perturbations
Stabilité de
de l'ordre
de plusieurs
minutes
long
terme
Figure 22. Classification des
différents types de la stabilité de système de
puissance.
Traditionnellement, le problème de la stabilité
a été de maintenir le fonctionnement synchrone des
générateurs du système. Ainsi, pour avoir une production
satisfaisante de la puissance électrique, toutes les machines synchrones
du système doivent fonctionner en synchronisme. Cet aspect de la
stabilité est influencé par les dynamiques de l'angle de rotor de
générateur et de la relation puissance-angle.
L'instabilité peut également avoir lieu sans
perte de synchronisme. Par exemple, un système composé d'un
générateur alimentant un moteur à induction peut devenir
instable en raison de l'effondrement de la tension de la charge. Dans ce cas,
c'est la stabilité et le contrôle de la tension qui créent
le problème, plutôt que le maintien du synchronisme. Ce type
d'instabilité peut aussi se produire dans le cas de charges couvrant une
vaste zone dans un grand système.
Un autre type d'instabilité peut avoir lieu : dans
l'éventualité d'un fort écart entre la puissance de la
charge et la puissance de la génération, les contrôleurs
principaux des générateurs et de la charge deviennent importants.
S'ils ne sont pas bien coordonnés, il est possible que la
fréquence du réseau devienne instable. Des unités de
générations et/ou de charges peuvent finalement être
déclenchées en entraînant une panne du système. Dans
ce cas, les générateurs peuvent rester en synchronisme mais le
système devient instable.
2.3.1- La stabilité de l'angle de rotor. 2.3.1.1-
Introduction.
Etant donné que la génération de
puissance électrique dépend principalement des machines
synchrones, un aspect important est le fonctionnement de ces
générateurs au synchronisme (Custem, 2002, II). Au
synchronisme, les rotors de chaque machine synchrone du système tournent
à la même vitesse électrique et les angles entre les champs
magnétiques, rotoriques et statoriques, restent constants.
En fonctionnement nominal équilibré, la
puissance électrique fournie par le générateur aux charges
est égale, en négligeant les pertes, à la puissance
mécanique fournie par la turbine.
Quand le système est perturbé, la puissance
électrique de la machine varie rapidement, mais la variation de
puissance mécanique fournie à la machine est relativement lente.
En raison de cette différence de vitesse de réponse, un
écart temporaire d'équilibre de puissance a lieu. Par
conséquent, ce déséquilibre de puissance entraîne
une variation des couples agissant sur le rotor. Ceci entraîne une
accélération ou décélération du rotor selon
le sens du déséquilibre, voire un glissement du champ de
synchronisme en entraînant une perte de synchronisme du
générateur avec le reste du système (Basler et
al., 2005). Si l'équilibre de puissance n'est pas rétabli,
la machine est mise hors service par une protection de survitesse ou de perte
de synchronisme, et la stabilité du système est mise en
danger.
Suite à une perturbation au système, le facteur
principal qui détermine l'évolution de l'état du
système est l'écart entre les angles de rotor. (Les angles sont
mesurés par rapport à une référence tournante au
synchronisme). Nous pouvons dire que les angles de rotor d'un système de
puissance peuvent évaluer selon deux scénarios (Anderson et
al., 2003) :
- Soit, les angles de rotor s'accroissent ensemble et oscillent
à l'unisson. Ils peuvent
éventuellement atteindre de nouvelles valeurs stables.
Tant que les écarts entre les
angles de rotor restent constants, le système reste
stable et il demeure au synchronisme.
- Soit, un ou plusieurs angles de rotor s'accroissent plus
rapidement que les autres. Alors, les écarts entre les angles de rotor
divergent dans le temps. Le système devient par conséquent
instable et il perd le synchronisme.
Pour conclure, nous pouvons dire que :
La stabilité de l'angle de rotor concerne la
capacité des machines synchrones d'un système de puissance
interconnecté de rester en synchronisme suite à une perturbation.
Elle dépend de la capacité de maintenir/restaurer
l'équilibre entre les couples électromagnétique et
mécanique agissant sur le rotor de chaque machine synchrone dans le
système. L'instabilité qui peut résulter se produit sous
forme d'augmentation des oscillations angulaires de certains
générateurs pouvant conduire à une perte de synchronisme
avec d'autres générateurs.
Suivant l'amplitude de la perturbation, nous pouvons
caractériser la stabilité de l'angle de rotor en deux
sous-catégories :
2.3.1.2- Stabilité angulaire aux grandes
perturbations (stabilité transitoire).
Elle concerne la capacité du
système de puissance de maintenir le synchronisme après avoir
subi une perturbation sévère transitoire tel un court-circuit sur
une ligne de transmission ou une perte d'une partie importante de la charge ou
de la génération. La réponse du système implique de
grandes variations des angles de rotor. Elle dépend de la relation
non-linéaire couples- angles.
La stabilité transitoire dépend non seulement de
l'amplitude des perturbations et du point de fonctionnement initial mais elle
dépend également des caractéristiques dynamiques du
système. Elle se manifeste à court terme sous forme d'un
écart croissant de façon apériodique de certains angles de
rotor. Si l'instabilité se manifeste directement suite à la
perturbation (plus précisément dans la première seconde
qui suit l'élimination du défaut), elle est appelée
instabilité de première oscillation (First Swing Instability),
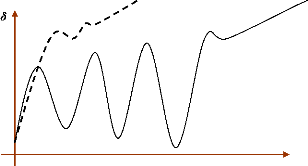
(cas 1, figure (23)), et elle s'étend sur 3 à 5 secondes.
L'instabilité transitoire peut aussi se manifester autrement. Elle peut
résulter de la superposition des effets de plusieurs modes d'oscillation
lents excités par la perturbation, provoquant ainsi une variation
importante de l'angle de rotor au-delà de la première oscillation
(instabilité de multi-oscillations), (cas 2, figure (23)). La gamme de
temps associée va de 10 à 20 secondes.
t (s)
Cas 2
Cas 1
Figure 23. Variation d'angle de
rotor.
Cas 1 : instabilité de première
oscillation. Cas 2 : instabilité de
multi-oscillations.
Le concept de stabilité transitoire peut être
expliqué par une approche graphique simple, à savoir le
critère d'égalité des aires (Equal Area Criterion). Cette
approche regroupe l'équation du mouvement et la courbe
(P-ä) traditionnelle représentant la relation entre la
puissance produite par le générateur et l'angle de rotor (Bergen
et al., 2000).
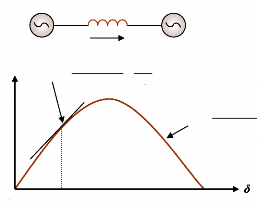
Pour expliquer cette approche, nous prenons un système
de puissance simple constitué d'un générateur synchrone
connecté à un jeu de barre infini via une ligne de transmission,
figure (24). Le générateur est modélisé par une
source de tension idéale Eg en série avec une
réactance Xg (modèle classique). La ligne et
le transformateur sont représentés par la réactance
XE.
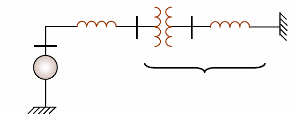
Eg?ä
Xg ETB ETH
XL
XT
XE = XT +
XL
Eo?0
Figure 24. Machine synchrone
connectée à un jeu de barre infini. 1- Relation
(P-ä) :
Dans l'état équilibré, la puissance produite
par le générateur Pe est donnée par
l'équation suivante :
E E
·
P (89)
g 0 · sin ä
e X X
g
=
+ E
Où, ä, l'angle de rotor (dit ici, l'angle
de puissance), est le déphasage entre la tension interne du
générateur (Eg) et la tension du jeu de barre
infini (E0). L'équation (89) est représentée
graphiquement à la figure (25).
0° äa äb 90° 180°
Figure 25. Relation puissance- angle de
rotor.

äb
äa

Lors de l'équilibre, la puissance électrique
Pe1 est égale à la puissance mécanique
appliquée pour l'angle correspondant äa.
Un brusque changement sur la charge du
générateur entraîne une variation de la puissance
mécanique, et par conséquent de la puissance électrique,
par exemple de Pe1 à
Pe2, figure (25). Le rotor va donc accélérer de sorte
que l'angle de puissance augmente, de äa à
äb, pour pouvoir fournir une puissance supplémentaire
à la charge. Cependant, l'accélération du rotor ne peut
pas s'arrêter instantanément. Ainsi, bien que la puissance
développée pour l'angle äb soit suffisante pour la
charge, le rotor va dépasser l'angle äb jusqu'à ce
qu'un couple opposé suffisant soit développé pour
arrêter cette accélération. L'énergie
supplémentaire va entraîner le ralentissement du rotor et la
diminution de l'angle de puissance. Suivant l'inertie et l'amortissement du
système, les oscillations de l'angle de rotor résultant vont ou
s'amortir, et la machine restera stable (cas 1, figure (26)), ou diverger, et
la machine deviendra instable en perdant le synchronisme avec le système
(cas 2, figure (26)).
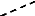
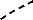
Cas 2
instable
Cas 1
stable

Figure 26. Variation d'angle de rotor.
2- Critère d'égalité des aires
:
Considérons un défaut, tel un défaut sur
la ligne de transmission, appliqué au système
précédent disparaissant après quelques périodes du
système. Ceci va modifier l'écoulement de puissance et, par
conséquent, l'angle de rotor ä. Retraçons la courbe
(P-ä) en tenant compte de ce défaut, figure (27). En
dessous de cette courbe, nous pouvons considérer deux zones, (Gholipour
Shahraki, 2003) :
- La première zone (zone A1, zone
d'accélération) se situe au-dessous de la droite horizontale
correspondante au point de fonctionnement initial (la droite de charge). Elle
est limitée par les deux angles de rotor (ä0 et
ä1) correspondants à l'apparition et à la
disparition de défaut. Cette zone est caractérisée par
l'énergie cinétique stockée par le rotor du fait de son
accélération : Pm > Pe.
- La deuxième zone (zone A2, zone de
décélération), qui commence après
l'élimination du défaut, se situe en dessus de la droite de
charge : elle est caractérisée par la
décélération du rotor : Pm <
Pe.
o P P
( m e
-
2 H
) (90)
d 2
dt

2
Si le rotor peut rendre dans la zone A2 toute l'énergie
cinétique acquise durant la première phase, le
générateur va retrouver sa stabilité. Mais si la zone A2
ne permet pas de restituer toute l'énergie cinétique, la
décélération du rotor va continuer jusqu'à la perte
de synchronisme.
0° ä0 ä1
ä2 180°
a
P
Région stable
aire 1 A2
Pm = Pe
Région instable
aire A1
Apparition
de défaut
Disparition
de défaut
0 ä
t1
t2
t
b
Figure 27. Courbes (a :
puissance-angle) et (b : variation d'angle de rotor) du
générateur
suite à un défaut de
transmission.
La relation entre les aires des zones (A1 et A2) et la
stabilité transitoire peut être mathématiquement
expliquée comme suit :
Rappelons tout d'abord que l'équation du mouvement de
générateur est donnée par la relation suivante :
H : la constante d'inertie.
ùo : la vitesse de synchronisme.
Pm : la puissance mécanique fournie au
générateur. Pe : la puissance
électrique du générateur.
dä
En multipliant cette équation par 2· , en
intégrant par rapport au temps et en faisant
dt
un changement de variables, nous obtenons :
? 2
2 ä
d ä ù
?
? ? ?? + = ? - ·
cte o (91)

( )
P P d ä m e
dt H
ä 0
ä0 : l'angle de rotor, initial, à l'instant
de l'application de défaut. ä2 : l'angle de rotor à
la fin de la période transitoire.
dä
Ainsi, lorsque : t = = =
0 0 ,
ä ä 0 la constante cte = 0.
dt
Après l'élimination du défaut, l'angle
ä va s'arrêter de varier et le générateur va
retrouver
dä
sa vitesse de synchronisme, lorsque = 0.
dt
Par conséquent, l'équation (91) s'écrit
comme suit :
ä2
? ( ) 0
P m P e dä (92)
- · =
ä 0
ä 1 ä 2
(93)
? - · + ? - · =
( ) ( ) 0
P m P e d ä P m P
e d ä
ä 0 ä 1
Où : ä1 est l'angle de rotor à
l'instant de l'élimination de défaut.
A1-A2=0 (94)
Ainsi, la limite de la restauration de la stabilité
transitoire se traduit mathématiquement par l'égalité des
aires de la zone A1 et de la zone A2 : cette condition est appelée
critère d'égalité des aires (Equal Area Criterion).
Par conséquent, les contrôleurs de la
stabilité transitoire peuvent améliorer la stabilité soit
en diminuant la zone d'accélération (zone A1), soit en augmentant
la zone de décélération (zone A2). Cela peut être
réalisé soit en augmentant la puissance électrique, soit
en diminuant la puissance mécanique.
En outre, un système statique d'excitation avec une
tension maximale élevée et d'un régulateur de tension
possédant une action "puissante" et rapide représente un moyen
très efficace et économique pour assurer la stabilité
transitoire (CIGRE, 1999). Enfin, une amélioration signifiante de la
stabilité transitoire est obtenue avec des systèmes très
rapides de détection des défauts et de disjoncteurs.
2.3.1.3- Stabilité angulaire aux petites
perturbations (stabilité dynamique).
Elle se définie par la capacité du
système de puissance de maintenir le synchronisme en présence des
petites perturbations. L'instabilité résultante se manifeste sous
forme d'un écart croissant, oscillatoire ou non-oscillatoire, entre les
angles de rotor.
La stabilité aux petites perturbations dépend du
point de fonctionnement d'équilibre initial du système ainsi que
des caractéristiques dynamiques du système. Contrairement
à la stabilité transitoire, elle ne dépend pas de niveaux
de perturbations, car celles-ci sont arbitraires et infiniment petites (Custem,
2002, II).
La relation puissance-angle (89) est une relation
non-linéaire en sinus. Mais pour des petites perturbations, la variation
de puissance reste approximativement proportionnelle à la variation de
l'angle ä. Des exemples typiques des petites perturbations
peuvent être donnés par des variations de niveau de 10 % de la
puissance mécanique appliquée à une machine du
système ou sur sa charge,... (Anderson et al., 2003).
La stabilité transitoire, comme nous l'avons vu, est
associée à la présence d'un couple synchronisant
suffisant, immédiatement après la perturbation. Si le
système est transitoirement stable, la stabilité aux petites
perturbations sera associée à la présence d'un couple
d'amortissement à la suite de la première oscillation. Si ce
couple est suffisant, les oscillations s'amortiront (amortissement positif).
Par ailleurs, si l'amortissement n'est pas suffisant, les oscillations vont
continuer, ou même elles vont augmenter (amortissement négatif
c.-à-d. manque de couple d'amortissement).
La perte de synchronisme peut avoir lieu entre une machine et
le reste du système (provoquant une instabilité locale), ou bien
entre des groupes des machines, dans lesquels chaque groupe peut garder son
synchronisme (désignant une instabilité globale).
L'instabilité aux petites perturbations se manifeste
à court terme, la gamme de temps associée étant de l'ordre
de 10 à 20 secondes.
Ce type de stabilité va être étudié en
détail dans la partie (§§-2.4) de ce chapitre. 2.3.2-
La stabilité de tension.
La stabilité de tension, par
définition, se rapporte à la capacité d'un système
de puissance, pour une condition de fonctionnement initiale donnée, de
maintenir des valeurs de tensions acceptables à tous les noeuds du
système après avoir subi une perturbation. La stabilité de
tension dépend donc de la capacité de maintenir/restaurer
l'équilibre entre la demande de la charge et la fourniture de la
puissance à la charge. L'instabilité résultante se produit
très souvent sous forme de décroissance progressive de tensions
à quelques noeuds.
Suite à une perturbation, certaines charges ont
tendance à restaurer la puissance consommée avant perturbation.
C'est le cas des moteurs asynchrones, des charges dont la tension est
contrôlée par un régleur en charge automatique, des
chauffages électriques commandé par thermostat, ... . Il existe
une puissance maximale transmissible entre les centres de production et ceux de
consommation. Cette puissance maximale disponible dépend non seulement
des caractéristiques du réseau de transport (distances
électriques) mais également de celles des
générateurs (possibilité de maintenir la tension
grâce à une réserve de puissance réactive
suffisante). Par conséquent, si la puissance que les charges tendent
à
restaurer devient supérieure à la puissance
maximale transmissible, le mécanisme de restauration des charges va
contraindre le réseau haute tension en augmentant la puissance
réactive consommée et en faisant donc baisser progressivement la
tension du réseau jusqu'à des valeurs inacceptables (Custem,
2002, II).
Généralement, l'instabilité de tension se
produit lorsqu'une perturbation entraîne une augmentation de puissance
réactive demandée au-delà de la puissance réactive
possible.
Plusieurs changements dans le système de puissance peuvent
contribuer à l'instabilité de tension, ce sont par exemple :
- une augmentation de charge.
- des générateurs, des condensateurs synchrones, ou
des SVCs (Static Var Compensator systems) qui atteignent les limites de
puissance réactive.
- une tentative d'un régleur automatique en charge ayant
échouée de restaurer la tension de charge à son niveau
initial avant la perturbation.
- une panne de générateur, une perte d'une charge
importante ou un déclenchement de ligne.
- une perte d'une source de puissance réactive
(condensateurs, machines synchrones,...).
La plupart de ces changements ont des effets significatifs sur
la production, la consommation et la transmission de puissance réactive,
ainsi sur la stabilité de tension. Par conséquent, des mesures
peuvent être utilisées pour améliorer la stabilité
de tension, tels (IEEE/PES, 2002) :
- un contrôle automatique des condensateurs shunts.
- un blocage des régleurs en charge automatique.
- une nouvelle répartition de la
génération.
- une replanification du fonctionnement des
générateurs et des noeuds de commande. - une régulation de
tension secondaire.
- un plan de délestage.
La gamme de temps de l'instabilité de tension
s'étend de quelques secondes à plusieurs minutes. Ainsi,
l'instabilité de tension peut être considérée comme
un phénomène à court terme (de l'ordre de plusieurs
secondes) ou, dans l'autre cas limite, comme un phénomène
à long terme (de l'ordre de plusieurs minutes).
Pour l'instabilité de tension à court terme
l'effondrement de tension se produit immédiatement après la
perturbation. Dans ce type d'instabilité, les charges et les
dispositifs, qui ont des caractéristiques spéciales de puissance
réactive tels les moteurs asynchrones sont souvent impliqués. Les
moteurs asynchrones consomment, juste après la perturbation, beaucoup de
puissance réactive pour assurer leur stabilité vis-à-vis
leurs charge. D'autres éléments peuvent aussi participer à
cette instabilité : les charges commandées
électroniquement, les convertisseurs HVDC, ... .
L'instabilité de tension à long terme se
développe lors d'un manque graduel de puissance réactive d'un
noeud ou une partie du système. Elle implique, quant à elle, des
équipements ayant une action plus lente tels les régleurs en
charge automatique, les charges commandées thermostatiquement, ... .
Il est aussi important de noter que l'instabilité de
tension ne se produit pas toujours toute seule. Souvent, l'instabilité
de tension et l'instabilité de l'angle de rotor se produisent ensemble,
l'une pouvant entraîner l'autre.
Enfin, la stabilité de tension peut être
classée en deux catégories ; la stabilité de tension aux
grandes perturbations et aux petites perturbations :
- Stabilité de tension aux grandes
perturbations. Le souci dans ce cas est de maintenir des tensions normales
aux noeuds de réseau électrique après une grande
perturbation. La stabilité est déterminée ici par les
caractéristiques du système et de charge, et par les interactions
entre les différents dispositifs de commande de tension dans le
système (Passelergue, 1998).
- Stabilité de tension aux petites
perturbations. Dans ce cas, les caractéristiques de la charge et des
dispositifs de commande déterminent la capacité du système
à maintenir les tensions équilibrées.
2.3.3- La stabilité de
fréquence.
La stabilité de la fréquence d'un
système de puissance se définit par la capacité du
système de maintenir sa fréquence proche de la valeur nominale
suite à une perturbation sévère menant par
conséquent à un important déséquilibre, entre les
puissances produite et consommée.
Le maintien de la fréquence à une valeur
nominale dans un système de puissance est lié à
l'équilibre global entre les puissances actives produites et
consommées (y compris les pertes).
Autrement dit, suite à certaines perturbations,
l'équilibre global des puissances produite- consommée peut
être déséquilibré : ce déséquilibre
entraîne alors une variation de fréquence.
L'énergie cinétique stockée dans les
pièces tournantes des machines synchrones et autres machines
électriques tournantes peut éventuellement compenser ce
déséquilibre. Si ce dernier n'est pas trop grand, les
générateurs participant à la commande de fréquence
régleront la puissance active fournie à travers leurs
réglages secondaires fréquence-puissance et ramèneront
ainsi l'écart de fréquence à des valeurs acceptables. Par
ailleurs, si le déséquilibre est trop grand, l'écart de
fréquence sera significatif avec des graves conséquences
(effondrement complet du système), (Andersson, 2006).
Lorsque la fréquence varie, les caractéristiques
de temps des processus et des différents dispositifs activés vont
varier de quelques secondes à quelques minutes. La stabilité de
fréquence peut donc être classifiée en
phénomènes à court terme et à long terme.
Dans un grand système de puissance et suite à un
incident sévère et, par la suite, à l'action de
protections (par exemple, un déclenchement de plusieurs lignes de
transmission), l'instabilité de la fréquence est
généralement associée à l'îlotage où
un scénario typique peut avoir lieu. Un ou plusieurs sous-réseaux
se retrouvent isolés du reste du système. Les
générateurs de chaque sous-réseau résultant
essayent de garder le synchronisme entre eux, mais la réserve tournante
est nettement insuffisante pour faire face à la charge connectée
au sous-réseau. La fréquence décroît ainsi
rapidement et l'instabilité produite est donc à court terme.
L'instabilité de fréquence peut également
se manifester à long terme, lorsqu'elle provient d'une mauvaise
réponse en puissance des centrales ou d'une mauvaise coordination entre
des régulations et protections (Custem, 2002, II).
2.3.4- Conclusion.
Dans cette partie, nous avons présenté les
définitions et les caractéristiques des différents types
de stabilité d'un système de puissance. Le concept
général de la stabilité peut se synthétiser en
trois groupes (stabilité de l'angle de rotor, de la tension et de la
fréquence). Cette classification est nécessaire pour mieux
comprendre les mécanismes :
- des phénomènes de l'instabilité du
système.
- des dispositifs nécessaires pour assurer la
stabilité du système.
Historiquement, les chercheurs et les ingénieurs des
systèmes de puissance mettaient l'accent sur la stabilité de
l'angle de rotor. Or les opérateurs des systèmes de puissance se
trouvent actuellement souvent obligés de faire fonctionner leurs
systèmes aux limites de la stabilité. L'amélioration de la
stabilité angulaire aux petites perturbations, en particulier
l'amortissement des oscillations interrégionales, est donc devenue un
objectif prioritaire : elle sera développée dans la partie
suivante de ce chapitre.
2.4- Etude de la stabilité angulaire aux petites
perturbations. 2.4.1- Introduction.
Les problèmes des oscillations à faibles
fréquences ont toujours été un sujet de
préoccupation. Mais pendant plusieurs décennies, les
ingénieurs des systèmes de puissance se sont
préoccupés beaucoup plus de la stabilité transitoire. Les
origines de cette dernière étaient faciles à identifier et
des mesures correctives ont été mises au point.
Les oscillations, qui sont typiquement dans la gamme de
fréquences de 0,2 à 2 Hz, peuvent être excitées par
des petites perturbations dans le système ou, dans certains cas, peuvent
même prendre naissance spontanément.
Ces oscillations limitent la capacité de transmission
de la puissance et, parfois, peuvent même causer la perte de synchronisme
et un effondrement de l'ensemble du système. Dans la pratique, en plus
d'assurer la stabilité, le système doit être bien amorti :
c.-à-d. les oscillations doivent être atténuées le
plus rapidement possible dès leurs apparitions.
La stabilité angulaire aux petites perturbations peut
être améliorée en faisant varier une grandeur
électrique :
- physiquement : de manière à augmenter le couple
d'amortissement agissant sur le rotor des machines synchrones.
- mathématiquement: de manière à
déplacer vers la partie gauche du plan complexe les
valeurs propres
complexes correspondant à une oscillation instable ou mal amortie.
Parmi les grandeurs que l'on peut moduler dynamiquement nous
nous intéressons au signal supplémentaire injecté dans
l'entrée de l'AVR par le stabilisateur de puissance (PSS). Il agit
à travers le régulateur sur le couple
électromagnétique de manière à renforcer sa
composante d'amortissement.
Dans la dernière partie de ce chapitre, nous allons
détailler les éléments importants de la stabilité
aux petites perturbations tels :
- le rôle de la variation du couple
électromagnétique.
- l'influence du système d'excitation.
- les différents types d'oscillations à faibles
fréquences.
- le PSS et ses méthodes de réglages et de
localisation.
2.4.2- Variation de couple
électromagnétique.
Dans un système de puissance, l'écoulement de
puissance est lié aux positions angulaires des rotors de
générateurs. Les positions des rotors doivent être
réglées à tout moment pour faire face à tout
changement de conditions de fonctionnement (variations de charge, de puissance
de sortie de turbine,...). Un déséquilibre entre les couples
mécanique et électromagnétique agissant sur le rotor,
provoque une variation du mouvement du rotor, par rapport à une
référence synchrone tournante. Ainsi, le couple
électromagnétique joue un rôle important dans la
stabilité angulaire. Ce couple est généralement produit
par les interactions entre les trois circuits du stator de
générateur, le circuit d'excitation et d'autres circuits tels les
enroulements amortisseurs (Anderson et al., 2003).
Suite à une perturbation, les variations du couple
électromagnétique peuvent s'exprimer en fonction des variations
d'angle de rotor Ää et de vitesse Äù,
suivant l'équation (95), (DeMello et al., 1969) :
Ä = + = ? Ä ä + ? Ä
ù
T e T S T A K S K A(95)
KS : coefficient de couple
synchronisant.
KA : coefficient de couple d'amortissent.
2.4.2.1- Couple synchronisant TS.
Donné par la composante, T S = K S ?
Ää, il représente la variation de couple
électromagnétique en phase avec la variation d'angle de rotor
Ää.
Le couple synchronisant est produit par les interactions entre
les enroulements du stator et la composante fondamentale du flux de l'entrefer.
Ce couple tend à accélérer ou
décélérer le rotor pour le ramener à sa position
initiale. Il agit comme un couple de rappel d'un ressort d'un système
mécanique, masse-ressort (IEEE, 2003).
Pour des petites déviations du point de fonctionnement,
le coefficient de couple synchronisant KS est représenté
par la pente de la courbe de la relation (puissance - angle), comme le montre
la figure (28).
E1?ä
E2?
0
Pe
X
K 1 2 cos 0
E E ä
=
S
P
X
ÄP e
=
ä
Ä
E E
1 2 sinä
=
X
0° ä0 90° 180°
Figure 28. La relation (puissance- angle)
du générateur et le coefficient de
couple
synchronisant.
Si äo est l'angle de puissance
à l'état équilibré, entre la tension interne du
générateur (E1) et la tension du jeu de barre infini
(E2), la pente de courbe à äo est
simplement la dérivée de la fonction puissance - angle :
|
K S
|
=
|
dP e
|
|
E1
|
· E 2
|
cos
|
äo
|
(96)
|
|
dä
|
ä o
|
|
X
|
|
|
|
|
|
|
|
|
Le couple synchronisant détermine alors la
capacité du système de supporter une grande perturbation sans
perdre le synchronisme : il est un facteur important pour la stabilité
transitoire. En cas des petites perturbations, le couple synchronisant
détermine la fréquence des oscillations.
2.4.2.2- Couple d'amortissement TA.
Donné par la composante, TA =
KA ? Äù, il représente la
variation de couple électromagnétique en phase avec la variation
de vitesse de rotor Äù.
Ce couple résulte généralement des
interactions entre la séquence positive du flux de l'entrefer et les
enroulements du rotor, plus particulièrement les enroulements
amortisseurs. Comme nous l'avons déjà vu, une variation de
l'angle de rotor ä entraîne une variation de vitesse de
rotor, Äù. D'après la loi de Faraday, la f.
é.m. induite est proportionnelle à la variation de vitesse.
Le courant induit par cette f. é.m. interagit avec le champ
électromagnétique du générateur, en produisant par
conséquent un couple d'amortissement naturel. Ce couple tend à
amortir les oscillations électromécaniques de la machine en
particulier suite à la première oscillation résultant
d'une grande perturbation (Anderson et al., 2003). Ainsi, il est
essentiel pour la stabilité aux petites perturbations, où le taux
d'amortissement des oscillations de rotor est primordial. Mais souvent, ce
couple est faible et parfois négatif surtout en présence de
contrôleurs tels les contrôleurs de tension (ces derniers sont
pratiquement les seules sources d'amortissement négatif). Un couple
négatif conduit à une croissance spontanée des
oscillations jusqu'à la perte de synchronisme.
Actuellement, les problèmes de stabilité angulaire
aux petites perturbations sont considérés associés
à l'amortissement insuffisant des oscillations.
2.4.3- Influence du système d'excitation sur la
stabilité angulaire.
La stabilité angulaire dépend des deux
composantes du couple électromagnétique, TS,
TA, pour chaque machine synchrone du système. La
littérature montre qu'une insuffisance de couple synchronisant conduit
à une instabilité apériodique ou non-oscillatoire, alors
qu'un manque de couple d'amortissement conduit à une instabilité
dynamique (IEEE/CIGRE, 2004).
De même, la littérature montre que le
système d'excitation avec son régulateur de tension a un impact
important sur les deux couples et par conséquent sur la
stabilité. Généralement, lorsqu'il y a des variations de
tension, les deux puissances active et réactive transmissibles dans le
réseau de transport vont varier. Cela entraîne des interactions
indésirables entre les régulateurs de fréquence (puissance
active) et de tension (puissance réactive).
Les systèmes d'excitation modernes, ayant une
réponse rapide et une action "puissante", peuvent augmenter le couple
synchronisant. Ceci améliore donc la stabilité transitoire. Mais
cet avantage peut être contrebalancé par l'impact négatif
du système d'excitation sur l'amortissement des oscillations en
diminuant couple d'amortissement (Yu, 1983).
Ainsi, le fonctionnement du système d'excitation est
perturbé par le conflit entre les contraintes du contrôle durant
les quelques premières périodes du réseau après la
perturbation et le laps de temps suivant. Pour cela, nous distinguons deux
types d'effet du système d'excitation, à savoir : l'influence sur
la stabilité transitoire et l'influence sur la stabilité aux
petites perturbations (Anderson et al., 2003).
2.4.3.1- Influence sur la stabilité
transitoire.
Comme nous l'avons déjà expliqué,
l'objectif principal de la stabilité transitoire est de maintenir le
synchronisme pendant et suivant une perturbation sévère. La
durée qui nous intéresse est relativement courte (quelques
secondes au maximum), la première oscillation ayant une importance
déterminante. Durant cette phase, le générateur est soumis
à une variation considérable de sa puissance électrique et
ainsi à une accélération (ou
décélération) de son rotor. Un système d'excitation
rapide et puissante peut faire varier très rapidement la tension interne
du générateur, durant cette phase. Ceci va augmenter la puissance
électrique et le couple synchronisant produits pendant la
première oscillation. Par conséquent, la puissance
électromagnétique disponible va entraîner une diminution
importante de l'accélération du rotor et de l'angle de rotor bien
avant d'atteindre la limite de la stabilité transitoire : la marge de
stabilité sera donc augmentée.
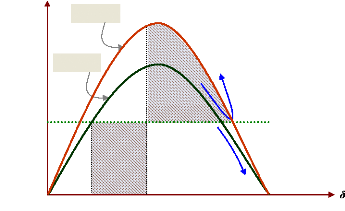
Pour montrer clairement l'effet positif d'un système
d'excitation rapide et puissante sur la stabilité transitoire, reprenons
le système précédent (machine synchrone connecté
à un jeu de barre infini, figure (24)).
La figure (29) montre les effets de deux types de système
d'excitation, à savoir : - un système lent et peu puissante
correspondant à la courbe A.
- un système rapide et puissant correspondant à la
courbe B, sur un défaut de transmission (Basler et al.,
2002).
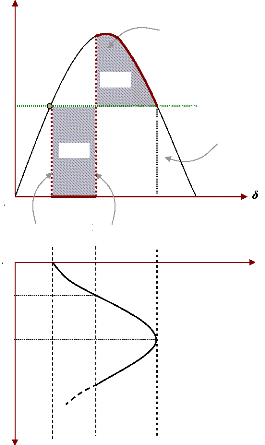
Cas B
Cas A
P
Pe-B
Maintenance du
synchronisme
Pm = Pe
Perte du
synchronisme
Pe-A
0° ä0 ä1 180°
ä2
Figure 29. Influence du système
d'excitation.
En comparant la zone hachurée située en dessous de
la droite de charge (zone d'accélération dans laquelle la
puissance électrique est moindre que la puissance mécanique)
avec la zone hachurée située au-dessus de la
droite de charge (zone de décélération), nous remarquons
que la condition d'égalité entre les deux zones n'est pas
assurée pour la courbe A. Par conséquent, la machine va perdre le
synchronisme.
Pour la courbe B, il est clair que la zone de
décélération est plus grande que la zone
d'accélération. La réserve de couple synchronisant permet
de restaurer la stabilité après l'élimination du
défaut.
Par conséquent, nous pouvons conclure que
l'augmentation du couple synchronisant, grâce à un système
d'excitation à gain élevé et réponse rapide,
augmente bien la puissance maximale transmissible pendant la phase transitoire,
et donc la marge de stabilité transitoire.
2.4.3.2- Influence sur la stabilité
dynamique.
L'action puissante et rapide du système d'excitation
pour améliorer la stabilité transitoire a malheureusement une
contribution négative importante sur l'amortissement des oscillations du
système.
Le courant d'excitation, qui agit pour améliorer le
couple synchronisant, est toujours en retard sur les caractéristiques
temporelles correspondantes aux parties électriques du
générateur et aux autres parties électriques du
système. A partir du moment de l'identification du changement
désiré d'excitation, le système d'excitation subit donc un
temps de retard inévitable. Pendant ce temps, l'état du
système oscillant va changer en impliquant un nouvel ajustement du
courant d'excitation. Le système d'excitation reste donc en retard, par
rapport au changement nécessaire. Par conséquent, le
système d'excitation va introduire l'énergie demandée
à contre temps. Les courants ainsi induits dans les circuits du rotor
s'opposeront aux courants induits initiés par l'écart de vitesse
du rotor (Äù). Le couple d'amortissement diminuera pouvant
atteindre des valeurs négatives : le comportement oscillatoire du
générateur va donc augmenter et une perte de stabilité
peut avoir lieu.
La figure (30) illustre l'influence du couple d'amortissement sur
la stabilité aux petites perturbations.
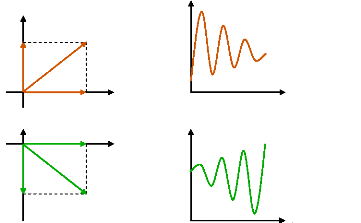
Ää
Ää
t
Système stable - TS positif
- TA positif
Système instable - TS positif
- TA négatif
t
Äù
TS
Ää
Äù
ÄTe
TA
TS
Ää
TA
ÄTe
Figure 30. Influence du couple
d'amortissement sur la stabilité.
2.4.4- Les différents types d'oscillations
à faibles fréquences.
Comme nous l'avons vu, les oscillations
électromécaniques sont associées aux rotors des
générateurs. Pendant ces oscillations, l'énergie
mécanique cinétique est échangée entre les
générateurs lors de l'écoulement de la puissance
électrique dans le réseau. Ces oscillations peuvent être
classées en deux groupes selon leurs manières d'évolution
:
- Oscillations spontanées. Dans ce cas, les
oscillations se développent lorsque l'amortissement d'un mode du
système devient négatif par changement graduel des conditions de
fonctionnement du système.
- Oscillations dues à une perturbation. Un
défaut de ligne de transmission, par exemple, peut entraîner des
oscillations en diminuant subitement l'amortissement d'un mode. Si cet
amortissement devient négatif, les oscillations résultantes vont
continuer ou même augmenter.
Les types des oscillations à faibles fréquences
rencontrées habituellement dans les systèmes de puissance peuvent
être classés en quatre groupes, figure (31).
Généralement, la fréquence de ces oscillations fournit une
bonne indication sur leurs types.
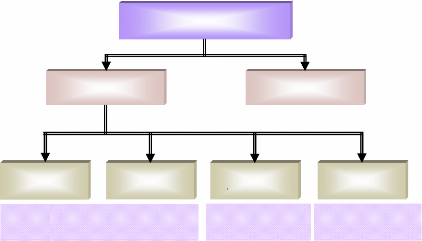
Modes électromécaniques
de 1 à 2 Hz de
0.2 à 1 Hz
Modes
locaux
Stabilité dynamique
Modes
interrégionaux
STABILITE DE L'ANGLE DE
ROTOR
Modes électriques
> 4 Hz
Modes
de contrôle
Stabilité transitoire
Modes mécaniques
> 4 Hz
de torsion
Modes
Figure 31. Classification de la
stabilité de l'angle de rotor. 2.4.4.1- Les oscillations
des modes locaux.
Les modes locaux sont les modes les plus rencontrés
dans les systèmes de puissance. Ils sont associés aux
oscillations entre un générateur (ou un groupe des
générateurs) d'une centrale électrique et le reste du
système. Le terme local est utilisé car les oscillations sont
localisées dans une seule centrale ou une petite partie du
système, (par exemple : les générateurs G1 et G2 oscillent
ensemble par rapport au générateur G3 trouvé dans la
même région, figure (32)). La gamme de fréquence de ces
oscillations est généralement de 1 à 2 Hz.
L'expérience montre que ces oscillations tendent
à se produire lors de l'utilisation des régulateurs de tension
possédant une réponse rapide et quand le lien de transmission
entre une centrale et ses charges est très faible (IEEE, 2003). Pour
assurer un bon amortissement de ces modes, des sources d'amortissement, tel le
stabilisateur de puissance, peuvent être ajoutées aux
générateurs à l'origine de ces modes.
2.4.4.2- Les oscillations des modes globaux.
Les oscillations des modes globaux, ou oscillations
interrégionales, sont associées à l'oscillation entre
certains générateurs d'une partie du système et certains
générateurs d'une autre partie du système (par exemple :
les générateurs, G1, G2, G3 et G4, de la région A
oscillent ensemble par rapport au générateur G5 de la
région B, figure (32)).
Les modes associés à ces oscillations
présentent généralement des amortissements très
faibles et, si ces derniers sont négatifs, de petites perturbations
peuvent exciter des oscillations divergentes. Les fréquences de ces
oscillations se trouvent généralement dans la gamme de 0.2
à 1 Hz. Cette gamme est inférieure à celle des modes
locaux car les réactances des liens entre les systèmes de
puissance sont élevées. Généralement, la
fréquence naturelle et le facteur d'amortissement d'un mode
interrégional décroissent lorsque l'impédance d'une ligne
d'interconnexion ou la puissance transmise augmente. Le système
d'excitation et les caractéristiques des charges affectent
également les oscillations des modes interrégionaux. Ainsi, ces
modes présentent des caractéristiques plus complexes que ceux des
modes locaux (CIGRE, 1996). Etant donné que les modes
interrégionaux impliquent plusieurs générateurs, un bon
amortissement de tels modes peut exiger l'utilisation de stabilisateurs de
puissance pour un grand nombre des générateurs (IEEE, 1990).
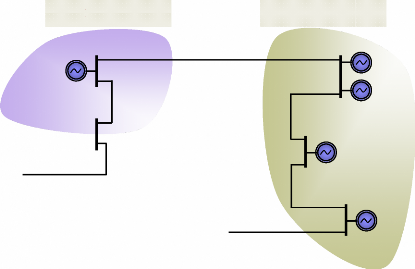
Région B Région
A
G3
G1
G2
G4
Figure 32. Système de puissance
simple à deux régions.
2.4.4.3- Les oscillations des modes de
contrôle.
Les oscillations associées aux modes de contrôle
sont dues :
- soit, aux contrôleurs des générateurs
(mauvais réglage des contrôleurs des systèmes d'excitation
ou des gouverneurs).
- soit, aux autres dispositifs contrôleurs (convertisseurs
HVDC, SVC,...).
La fréquence de ces oscillations est supérieure
à 4 Hz. 2.4.4.4- Les oscillations des modes de
torsion.
Ces oscillations sont essentiellement reliées aux
éléments en rotation entre les générateurs et leurs
turbines. Elles peuvent aussi être produites par l'interaction des
éléments de rotation avec le contrôle d'excitation, le
contrôle de gouverneur, les lignes équipées avec des
compensateurs de condensateurs en série,... . La fréquence de ces
oscillations est aussi supérieure à 4 Hz.
2.4.4.5- Conclusion.
Dans le cadre de cette étude, nous nous
intéressons seulement aux modes locaux et aux modes
interrégionaux : appelés modes électromécaniques.
La distinction claire entre les modes locaux et interrégionaux
s'applique principalement aux systèmes qui peuvent être
divisés en régions distinctes séparées par de
longues distances. Par ailleurs, pour les systèmes où les
centraux sont distribués uniformément sur une large région
géographique, il est difficile de distinguer entre les modes locaux et
interrégionaux à partir de considérations
géographiques. Cependant, une conclusion commune considère que
les modes interrégionaux ont les fréquences les plus basses et
que la plupart des générateurs du système y
contribuent.
2.4.5- L'amortissement.
Nous avons vu que les oscillations
électromécaniques limitent la capacité de transmission de
puissance dans les réseaux électriques. Elles peuvent parfois
entraîner une perte de synchronisme ou même un black-out dans le
système entier. Par conséquent, des sources spécifiques
d'amortissement sont indispensables pour assurer un fonctionnement fiable du
système.
La stabilité peut être considérablement
améliorée en utilisant des systèmes en boucle
fermée avec des systèmes de contrôle adaptés. Au fil
des années, un effort de recherche important était
effectué pour une meilleure conception de tels contrôleurs. Il y a
principalement deux moyens rapides permettant d'améliorer la
stabilité :
- l'utilisation d'un contrôleur côté
générateur : signal de contrôle supplémentaire dans
le système d'excitation du générateur.
- l'utilisation d'un contrôleur côté lignes
de transmission : signal de contrôle
supplémentaire dans les systèmes FACTS (Flexible AC
Transmission System).
Dans le premier cas, le problème d'oscillations
électromécaniques est résolu en ajoutant au
générateur un contrôleur spécifique appelé :
(Power System Stabilizer (PSS)). Ce contrôleur détecte les
variations de vitesse de rotor ou de puissance électrique du
générateur et applique un signal, adapté, à
l'entrée du régulateur de tension (AVR). Le
générateur peut ainsi produire un couple d'amortissement
additionnel qui compense l'effet négatif du système d'excitation
sur les oscillations (Kundur, 1994).
Les systèmes FACTS, qui sont des dispositifs
basés sur les récentes avancées en électronique de
puissance, peuvent être modifiés pour participer à
l'amortissement des oscillations électromécaniques. Les
systèmes FACTS (tels SVC (Static VAR Compensator), TCSC (Thyristor
Controlled Series Capacitor), SSSC (Static Synchronous Series Compensator),...)
sont principalement placés dans le système de puissance pour
différentes raisons, (tels le contrôle des transits de puissance,
des échanges de puissance réactive, les tensions de
réseau, ...). Toutefois, un contrôleur et un signal de
stabilisation supplémentaires peuvent être ajoutés pour
améliorer la stabilité. Outre ces principaux rôles, les
FACTS peuvent alors satisfaire les problèmes de la stabilité
(Rogers, 2000; Sadeghzadeh, 1998).
Ces systèmes restent très chers pour être
installés uniquement pour une raison d'amortissement des
oscillations.
Les contrôleurs PSSs qui sont des systèmes
simples et faciles à installer, pratiques, efficaces et moins chers,
sont les systèmes les plus utilisés pour améliorer la
stabilité aux petites perturbations. Nous allons donc les utiliser dans
notre étude.
2.4.5.1- Fonctionnement et modèle de
PSS.
Un PSS permet d'ajouter un signal de tension proportionnel
à la variation de vitesse de rotor dans l'entrée du
régulateur de tension (AVR) du générateur, figure (33). Un
couple électrique en phase avec la variation de vitesse de rotor est
ainsi produit dans le générateur. Par conséquent, avec un
système d'excitation rapide et fort, l'avantage présenté
par un couple synchronisant important est toujours assuré et le
problème de la décroissance du couple d'amortissement est
corrigé (Rogers, 2000; IEEE, 2003). Le PSS va s'opposer à toutes
les faibles oscillations en forçant le système d'excitation
à varier au plus juste et au bon moment.
Par conséquent, l'ensemble du système de
contrôle d'excitation (AVR et PSS) doit assurer les points suivants
(Kundur et al., 1989) :
- supporter les premières oscillations faisant suite
à une grande perturbation ; c.-à-d. assurer la stabilité
transitoire du système.
- maximiser l'amortissement des oscillations
électromécaniques associées aux modes
locaux ainsi
qu'aux modes interrégionaux sans effets négatifs sur les autres
modes.
- minimiser la probabilité d'effets défavorables,
à savoir :
o les interactions avec les phénomènes de hautes
fréquences dans le système de puissance telle la résonance
dans le réseau de transport.
o les instabilités locales dans la bande de l'action
désirée du système de contrôle. - être
suffisamment robuste pour permettre au système de contrôle
d'assurer ses objectifs pour divers points de fonctionnement probables du
système de puissance.
Le choix du signal d'entrée de PSS représente une
étape critique dans la conception du PSS. Plusieurs
considérations interviennent dans ce choix, telles :
- la sensibilité du signal d'entrée aux
oscillations électromécaniques (autrement dit, les modes
oscillatoires doivent être "observables" dans le signal choisi).
- l'insensibilité du signal d'entrée du PSS
à son propre signal de sortie. D'une façon similaire, la
sensibilité doit être très la plus faible possible pour les
signaux de sortie d'autres PSSs.
Un bon résultat peut être obtenu si
l'entrée du PSS est la variation de la vitesse de rotor
(Äù), la variation de puissance produite du
générateur (ÄPe) ou la fréquence
du jeu de barre
(Äf). Etant donné que le PSS est
utilisé pour produire un couple électrique proportionnel à
la variation de vitesse, il apparaît donc plus convenable d'utiliser la
variation de vitesse (Äù) comme entrée du PSS.
Cependant, quel que soit le signal d'entrée, la fonction de transfert du
PSS doit compenser les caractéristiques de phase du système
d'excitation, des parties électriques du générateur et des
autres parties électriques du système. L'ensemble de ces
dernières déterminent la fonction de transfert entre
l'entrée du système d'excitation (Ä Ver)
et le couple électrique du générateur
(ÄTe), (Larsen et al., 1981, I). Cette
fonction de transfert est dénotée GEP(s),
figure (33).

Partie
mécanique
du
générateur
_
Vref
+
+
VS
ÄVer
Vt
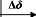
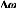
ÄTm
Système
d'excitation/
Régulateur
Partie
Efd électrique
du
générateur
+
ÄTe
_

PSS
Figure 33. Modèle simplifié
de liaison entre un PSS et le système.
Le type de PSSs le plus utilisé est connu sous le nom
de PSS conventionnel (ou PSS avance/retard). Ce type a montré sa grande
efficacité dans le maintien de la stabilité aux petites
perturbations. Ce PSS utilise la variation de vitesse de rotor comme
entrée. Il se compose généralement de quatre blocs, figure
(34) :
- un bloc d'amplificateur.
- un bloc de filtre passe-haut "filtre washout".
- un bloc de compensation de phase.
- un limiteur.
VS
max
VS
VS
min
_
_
Äù
KPSS
1 +
ST W
ST W
1+
1+
ST2
ST1
1+
1+
ST4
ST3
Bloc
avance/retard
Gain Filtre
Washout
Figure 34. Modèle d'un PSS
avance/retard.
1- L'amplificateur
Il détermine la valeur de l'amortissement introduit
par le PSS. Théoriquement, sa valeur (KPSS)
doit correspondre à l'amortissement maximal. Toutefois, la valeur du
gain doit satisfaire l'amortissement des modes dominants du système sans
risquer de dégrader la stabilité des autres modes ou la
stabilité transitoire (Kundur et al., 1989).
Généralement, KPSS varie
généralement de 0.01 à 50 (IEEE, 1990).
2- Le filtre passe-haut "filtre washout"
Il élimine les oscillations à très basse
fréquence (inférieure à 0.2 Hz) présentées
dans le signal d'entrée. Il supprime également la composante
continue de la vitesse (la composante "DC" correspondant au régime
statique) : le PSS ne réagit donc que lorsqu'il y a des variations de
vitesse. La constante de temps de ce filtre (TW) doit
être suffisamment grande pour permettre aux signaux, dont la
fréquence est située dans la bande utile, d'être transmis
sans atténuation. Mais, elle ne doit pas être trop grande pour
éviter de mener à des variations indésirables de tension
de générateur pendant les conditions d'îlotage.
Généralement, TW varie de 1 à 20
secondes (Basler et al., 2005; IEEE, 2003). Une amélioration
remarquable sur la stabilité de la première oscillation est
obtenue avec une valeur TW fixée à 10
secondes (Pal et al., 2005).
3- Le filtre compensation de phase
L'origine de l'amortissement négatif est, comme nous
l'avons vu, associée au retard de phase introduit entre le couple
électrique du générateur (ÄTe) et
l'entrée du système d'excitation (ÄVer).
Par conséquent, le PSS fournit l'avance de phase nécessaire pour
compenser le retard de phase de la fonction de transfert
GEP(s). Pratiquement, un bloc de phase d'avance pure ne
suffit pas pour réaliser la compensation de phase nécessaire ;
ainsi, un bloc d'avance/retard de phase est souvent utilisé. Pour mieux
garantir la stabilité du système, deux étages (au moins)
de compensations de phase sont nécessaires. La fonction de transfert de
chaque étage est une simple combinaison de pole-zéro, les
constantes de temps d'avance (T1,
T3) et de retard (T2,
T4) étant réglables. La gamme de chaque
constante de temps s'étend généralement de 0.01 à 6
secondes (Basler et al., 2005). Mais pour des considérations de
réalisation physique, les constantes de temps de retard (T2,
T4) sont considérées fixes et généralement
autour de la valeur de 0.05 secondes (Fleming et al., 1981).
4- Le limiteur
Le PSS est conçu pour améliorer l'amortissement
du système en cas de petites variations autour d'un point
d'équilibre. Son objectif n'est pas de restaurer la stabilité du
système aux perturbations sévères (la stabilité
transitoire). Le PSS a parfois tendance à perturber le bon
fonctionnement du régulateur de tension en le saturant lorsque ce
dernier essaye de maintenir la tension lors de conditions transitoires. Ainsi,
le PSS doit être équipé d'un limiteur afin de
réduire son influence indésirable durant les phases transitoires
(Larsen et al., 1981, II). Les valeurs minimales et maximales du
limiteur s'étendent de #177; 0.02 à 0.1 per-unit (IEEE, 1990).
2.4.5.2- Réglage des paramètres de
PSS.
Le problème de la conception d'un PSS est de
déterminer les valeurs de ses paramètres pour :
- augmenter l'amortissement des modes du système.
- assurer une stabilisation robuste.
La minimisation des risques probables des interactions
défavorables et des effets négatifs sur les autres modes
oscillatoires du système représente aussi un point critique
important qui influence le réglage de PSSs. En outre, les valeurs des
paramètres du PSS doivent être réglées sans
entraîner d'effet négatif dans la restauration de la
stabilité transitoire.
De nombreuses méthodes sont proposées dans la
littérature pour le réglage des paramètres de PSS.
Généralement, la plupart de ces méthodes sont
basées sur l'analyse des valeurs propres du système.
2. 4. 5. 2. 1- Méthode de compensation de
phase.
Pour expliquer le réglage des paramètres de PSS
par la méthode de compensation de phase, nous prenons un système
simple consistant en un générateur connecté à un
jeu de barre infini, figure (24). Le modèle linéaire de ce
système peut être graphiquement illustré par la
représentation de Heffron-Philips (Pal et al., 2005), comme le
montre la figure (35).
Les termes K1, ..., K6 sont les constantes de
linéarisation.
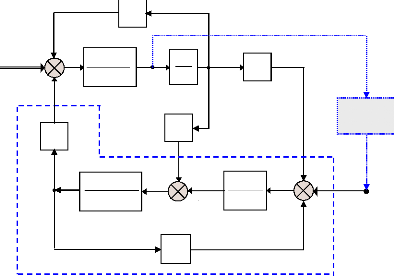
ÄTm +
ÄTe2
ÄTe1 _
ÄEq'
K2
_
K3
1 sT K
+ d' 0 3
1
D 2 Hs
+
K1
Äù
_
K6
K4
ù0
s
ÄEfd
+
Ä
ä K5
Ka
1+ sTa
GEP(s)
_
_
+
ÄVs
GPSS(s)
Figure 35. Modèle de
Heffron-Philips d'un système
(monomachine - jeu de barre
infini).
L'objectif principal d'un PSS est d'introduire une composante
d'un couple électrique sur le rotor de la machine synchrone ; ce couple
est proportionnel à l'écart entre la vitesse actuelle du rotor et
la vitesse de synchronisme. Lorsque le rotor oscille, ce couple agit comme un
couple d'amortissement pour atténuer les oscillations.
La fonction de transfert GEP(s) et le retard
de phase de la boucle électrique peuvent être
dérivés du modèle de Heffron-Philips. Ils sont
donnés par les deux relations suivantes (Yu, 1983) :
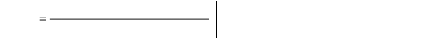
'
)
+ K K K a 3 6
sT K
do 3
GEP s
( )
K K K
a 3 2
(1 )(1
+ +
sT a
(97)
s ë ó j ù
= = +
PhiGEP GEP s s = ë = ó +
j ù
= ? ( ) (98)
Avec ë= ó + jù est
la valeur propre calculée pour le système sans signal de
stabilisation.
Pour simplifier, nous considérons que les
paramètres à régler du PSS sont le gain
Kpss et les constantes de temps T1 et T3
(avec T1 = T3) ; les autres paramètres sont fixés (avec
T2 = T4). Ainsi, la fonction de transfert de PSS peut se
réécrire comme suit :
|
G s K
PSS PSS
( ) =
|
2
sT ? 1 + sT ?
w ? 1 K G s
? = . ( ) (99)
PSS f
1 + sT 1 sT
w ? + 2 ?
|
Etant donné que l'avance de phase du PSS
(PhiGPSS) est égale à la phase
PhiGEP, la constante de temps T1 est
donnée, tout calcul fait, par la relation suivante :
tan( )
â
T = T = (100)
1 3ù ó â
- · tan( )
1 ? 1 1 1 2
? ù ? ù ? ù
?
- - -
? T ? T ?
w
Avec, â = - -
?? Phi tan tan ? ? + ? ?
?? (101)
GEP ?? ?? + 2 tan
2 ó
? ?1+óT? ? 1 + ó T
w 2 ? ?
Le gain du PSS, quant à lui, est donné par la
relation suivante (Yu, 1983) :
=
4ùæH
n
GEP s
( )
G s f ( )
(102)
KPSS
K2
s=ë=ó
+jù

ù 1
o K
Avec, ù = (103)
n2 H
ùo : la vitesse de synchronisme du
système, en rad/s.
ùn : la pulsation naturelle
d'oscillation en rad/s.
La valeur ùn représente la
solution de l'équation caractéristique de la boucle
mécanique (figure (33)). Elle est définie par l'équation
suivante (coefficient d'amortissement D négligée).
2 + ù 1 = 0 , , = #177; ù
Hs o K avec s j n
2 (104)
2. 4. 5. 2. 2- Méthode du
résidu.
Nous avons vu que le filtre avance/retard du PSS est
utilisé pour compenser le retard de phase de la fonction de transfert
GEP(s). En déterminant la valeur du retard de phase,
nous pouvons ainsi calculer les constantes de temps (avance/retard)
nécessaires pour assurer la compensation demandée. Pour ce faire,
l'angle de phase de résidu peut être utilisé (Aboul-Ela
et al., 1996; Cai, 2004). Considérons la forme suivante de la
fonction de transfert du PSS pour un système à une
entrée/une sortie :
|
sT ?1+sT ?
W 1
H s K
( ) = · ·
PSS 1 sT ?? 1 sT ??
+ +
W 2
|
m
|
(105)
|
Où : m est le nombre d'étages de
compensation (généralement m = 2).
La figure (36) montre l'effet du résidu sur le
déplacement de valeur propre dans la partie gauche du plan complexe.
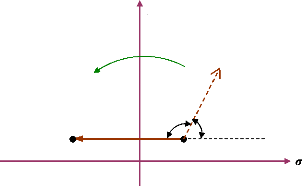
fù
Direction de rotation
Direction de Ri
öcom arg (Ri)
ëi 0
ëi 1
Äëi
Figure 36. Déplacement de valeur
propre par la rotation du résidu associé.
L'angle de phase öcom,
nécessaire pour diriger la direction du résidu Ri de
sorte que la valeur propre associée ëi se déplace
parallèlement à l'axe réelle, peut être
calculé par l'équation suivante :
? com =180°-arg(R i ) (106)
Où : arg(Ri) est l'angle de phase du
résidu Ri.
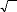
á
ù ·
i
T 1
2 (107)
=
|
Avec :
|
á
|
=
|
1 sin
-
|
? ? ?
com
? ?
? m ?
|
(108)
|
|
1 sin
+
|
? ? ?
com
? ?
? m ?
|
1 = á · T 2
T ,
Par conséquent, les constantes de temps T1 et
T2, du bloc avance/retard nécessaires pour obtenir l'angle
öcom, peuvent être calculées comme suit
(Aboul-Ela et al., 1996) :
Où : ùi est la fréquence du
mode ëi en rad/sec.
Pour calculer le gain KPSS, nous pouvons
réécrire la fonction transfert du PSS comme suit :
H(s) = K PSS ·
Hf(s) (109)
Le déplacement des valeurs propres est donné par
l'équation (82) que nous rappelons ci- dessous :
Äë i = ë i - ë i =
R i H ë i
1 0 ( ) (110)
En remplaçant l'équation (109) dans la
dernière équation, nous obtenons pour gain
KPSS la valeur littérale suivante (Sadicovic et
al., 2006) :
ë ë
i i
1 0
-
K PSS
Ri
· H f
( )
ë i
(111)
Une autre méthode peut être utilisée pour
régler le gain KPSS : la méthode traditionnelle de
Ziegler et Nichols basée sur l'étude du régime critique de
la réponse harmonique du système en boucle fermée. On
cherche ainsi le gain produisant l'instabilité. Le test consiste
à augmenter lentement le gain de stabilisateur jusqu'à
l'observation de l'instabilité. Pour un signal d'entrée de type
variations de vitesse, ce test doit être effectué avec une charge
maximale et des conditions de transport d'énergie satisfaisantes. Le
savoir-faire montre, en général, que le gain désiré
représente le tiers du gain à l'instabilité : Kst
= Kinst / 3, (Larsen et al., 1981, III).
2.4.5.2.3- Méthode de placement des
pôles.
Cette méthode consiste à déterminer les
valeurs des paramètres d'un PSS de sorte que tous les pôles du
système en boucle fermée se trouvent placés en des
positions spécifiées préalablement dans le plan
complexe.
Cette méthode peut être mathématiquement
décrite en considérant la représentation suivante du
système (Fleming et al., 1981; Aström et al.,
1996), figure (37).
Système
ÄV +
+
H(s)
G(s)
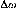

PSS
Figure 37. L'ensemble (système-PSS)
en boucle fermée.
Où : G(s) est la fonction de
transfert du système entre le signal de référence Ä
V du régulateur de tension de générateur,
où le PSS doit être installé, et la variation de vitesse de
rotor Äù.
H(s) est la fonction de transfert de PSS.
Les pôles de G(s) sont justement les
valeurs propres du système linéarisé en boucle ouverte. La
fonction de transfert du système entier en boucle fermée
F(s) devient :
=
F s
( )
1( ) ( )
- ·
G s H s
G s
( )
(112)
Les valeurs propres du système en boucle fermée
sont les pôles de la fonction de transfert F(s) ; elles
doivent satisfaire l'équation caractéristique suivante :
1-G(s)·H(s)=0 (113)
1
H s = (114)
( )
G s
( )
Si ë i , i = 1,2,L n
sont les valeurs propres spécifiées préalablement,
l'équation (114) peut ainsi se réécrire comme suit :
1
H ë
( )
ë = (115)
i G ( )
i
ë T 1 + ë T 1 + ë T
1
i W i 1 i 3
·
K · ·=
PSS 1 4
+ ë 1 1 ( )
i T W + ë i T + ë
ë
2 i i
T G
|
(116)
|
Par conséquent, nous obtenons un ensemble
d'équations algébriques linéaires. En résolvant ces
équations, nous pouvons déterminer les valeurs des
paramètres désirés du PSS qui assurent le placement
précis des valeurs propres.
2.4.5.3- Emplacement optimal des PSSs.
Tous les générateurs du système ne
participent pas aux modes dominants : tous les générateurs n'ont
donc pas besoin d'être équipés de PSSs. En outre, il faut
tenir compte des interactions négatives entre les PSSs qui augmentent
avec le nombre de ces derniers. Enfin, il faut tenir compte des critères
économiques.
Ainsi, la première étape de la mise en oeuvre
des PSSs, est de trouver les emplacements optimaux des PSSs nécessaires
et de déterminer leur nombre. Ce problème a fait l'objet, depuis
une dizaine d'années, d'un grand nombre de recherche
(Pérez-Arriaga et al., 1982; Hsu et al., 1987; Tse
et al., 1988; Ostojic, 1988; Pagola et al., 1989; Jin Lu et
al., 1990; Feliachi, 1990 ). Les approches les plus efficaces
proposées sont basées sur l'analyse modale du système
linéarisé :
- le mode shape.
- les facteurs de participations.
- les résidus.
Comme nous l'avons vu, les amplitudes des résidus
associés aux modes dominants de la fonction de transfert du
système en boucle ouverte peuvent être utilisées pour
déterminer les
placements les plus efficaces pour installer les PSSs. Les
amplitudes des facteurs de participation ou du mode shape permettent de
déterminer l'influence de chaque variable d'état dans les modes
oscillatoires associés. Ces méthodes peuvent donc nous fournir
des indications importantes sur l'emplacement optimal des PSSs dans le
système pour réaliser un meilleur amortissement par rapport
à des critères donnés.
Sachant que des emplacements différents des PSSs
entraînent des oscillations totalement différentes, des PSSs "mal
placés" peuvent donc ne pas répondre aux objectifs. Pour cela, il
faut bien choisir la méthode qu'il faut appliquer pour déterminer
les bons emplacements des PSSs. Les méthodes mentionnées
ci-dessus donnent généralement de bons résultats, mais la
recherche de méthodes plus efficace reste toujours actuelle.
2.5- Conclusion.
Dans ce chapitre, nous avons présenté d'une
façon générale les différents types de
stabilité. Nous avons présenté également une
analyse fine sur la stabilité aux petites perturbations et les
oscillations électromécaniques présentes dans les
systèmes de puissance. Cette étude nous a ainsi permis de mettre
en évidence les points importants suivants :
- Un système de puissance doit présenter un point
d'équilibre stable dans les conditions de fonctionnement normales.
- Un système de puissance est stable s'il retrouve un
état d'équilibre acceptable après avoir été
soumis à une perturbation.
- La stabilité angulaire aux petites perturbations est
habituellement considérée comme la capacité du
système de puissance à maintenir le fonctionnement synchrone des
générateurs pour de faibles variations des charges et des
sources.
- Les oscillations électromécaniques sont
généralement dues aux modes naturels du système. Ainsi,
nous ne pouvons pas les éliminer. Cependant, leurs fréquences et
leurs amortissements peuvent toujours être modifiés.
- Suite à une perturbation, le système de puissance
peut être transitoirement stable mais il peut présenter par la
suite des oscillations divergentes.
- Suite à une grande perturbation, le régulateur
de tension du système d'excitation de générateur, ayant
une action puissante et rapide, contribue efficacement à augmenter les
puissances électriques des générateurs pendant la
première oscillation. Cela contribue à diminuer la puissance
d'accélération du générateur en augmentant le
couple synchronisant. En conséquence, la plage de stabilité
transitoire est bien améliorée. Malheureusement, cet avantage est
contrebalancé par l'impact négatif du système d'excitation
sur l'amortissement des oscillations en diminuant le couple d'amortissement.
- Les oscillations interrégionales sont
associées aux lignes d'interconnexion de grande impédance et une
demande de puissance à transmettre élevée. Comme ces
oscillations se produisent entre plusieurs régions du système,
leurs caractéristiques sont plus complexes que celles des oscillations
des modes locaux et elles sont plus difficiles à amortir.
- Les stabilisateurs de puissance (PSSs), par leur
efficacité et leur coût réduit, sont les moyens habituels
non seulement pour éliminer les effets négatifs des
régulateurs de tension, mais aussi pour amortir les oscillations
électromécaniques du système. En
outre, l'amortissement assuré par les PSSs permet au
système de fonctionner au-delà même de la limite de la
stabilité à l'état équilibré.
- Le réglage des paramètres des PSSs et leurs
emplacements sont des facteurs critiques pour pouvoir assurer convenablement le
bon fonctionnement des PSSs.
Ce dernier point fera l'objet du chapitre quatre. Dans le
troisième chapitre, nous présentons tout d'abord les principes
généraux d'optimisation par algorithmes génétiques
; nous les utilisons par la suite.
| 

